OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
MATEMATIČKA INDUKCIJA
U nauci postoje dva osnovna načina zaključivanja: dedukcija (lat. deduction-izvođenje) i indukcija (lat. induction-uvođenje). Deduktivni način razmišljanja bazira se na pronalaženju opštih rešenja pomoću kojih rešavamo pojedinačne probleme. Za razliku od dedukcije, indukcija je zaključivanje kojim se iz stavova koji se odnose na ograničen broj pojedinačnih slučajeva iste vrste izvodi jedan opšti stav, tj. stav koji se odnosi na sve slučajeve te vrste. Ovakav metod zaključivanja takođe se naziva i nepotpuna ili empirijska indukcija. Ovom metodom može se doći kako do tačnih tako i do netačnih zaključaka (ili do zaključaka koji su tačni samo za određen broj slučajeva). Uprkos tome, indukcija je izuzetno značajna u eksperimentalnim prirodnim naukama gde je dovela do mnogih značajnih saznanja. Nepotpuna indukcija u matematici pomaže da se otkrije neka činjenica, koju zatim treba i dokazati, npr. matematičkom indukcijom.Metod matematičke indukcije je poseban metod matematičkog dokazivanja koji nam ne dozvoljava da donosimo zaključke o opštem pravilu na osnovu pojedinačnih slučajeva, bez određenih dokaza.
Značaj sinteze indukcija-dedukcija dobro je formulisao ruski matematičar A. J. Hinčin (1894-1959) čija misao glasi:
“Onaj koji praktikuje indukciju ne odevajući se u formalna pravila (tj. ne vršeći njenu sintezu sa deduktivnom formom), prestaje da bude matematičar; on se bavi empirijskim uopštavanjem bez ikakve veza sa matematičkom naukom. Obratno, vršeći dedukciju neoplođenu induktivnim sadržajem, matematičar prestaje da stvara zato što bez elementarne indukcije, tj. bez dobijanja opštih zaključaka na osnovu pojedinačnog materijala, nema i ne može biti naučnog stvaralaštva. Nauka počinje tamo gde po prvi put srećemo uopštenje.”
Pri strogom zasnivanju teorije brojeva aksioma prirodnih brojeva koju nazivamo aksiomom matematičke indukcije osnova je jednog karakterističnog rasuđivanja u matematici koje nazivamo metod matematičke indukcije. Ta aksioma glasi ovako:
Ako je A podskup skupa N sa osobinom:
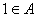 ,
,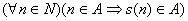 ,
,
onda je A=N.
(![]() je
oznaka za funkciju sledbenik)
je
oznaka za funkciju sledbenik)
Ovo tvrđenje pruža mogućnost za dokazivanje velikog broja tvrđenja koja
se odnose na prirodne brojeve.
Metod matematičke indukcije, često nazivan i principom matematičke indukcije,
sastoji se u sledećem:
Neka je ![]() iskaz koji se odnosi na prirodan broj
iskaz koji se odnosi na prirodan broj ![]() .
Tada je on tačan za sve prirodne brojeve ako su ispunjeni uslovi:
.
Tada je on tačan za sve prirodne brojeve ako su ispunjeni uslovi:
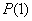 je tačan iskaz,
je tačan iskaz,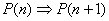 je tačan iskaz za sve
je tačan iskaz za sve 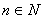 .
.
Korišćenjem formalnog jezika princip matematičke indukcije se može napisati:
![]() .
.
Valjanost principa matematičke indukcije počiva na sledećem, očigledno
ispravnom rasuđivanju:
Ako je tačno ![]() ,
onda s obzirom da je tačno
,
onda s obzirom da je tačno ![]() (uslov b) za
(uslov b) za ![]() ),
tačno je i
),
tačno je i ![]() .
Iz tačnosti
.
Iz tačnosti ![]() ,
tačno je i
,
tačno je i ![]() ,
itd. Zaključujemo da je
,
itd. Zaključujemo da je ![]() tačno za
tačno za ![]() .
.
Stoga, princip matematičke indukcije usvajamo kao tačan.
U matematičkoj praksi se upotrebljavaju izvesni nazivi za delove formule
![]()
![]() .
Tako se formula
.
Tako se formula ![]() naziva osnova (baza) indukcije, a implikacija
naziva osnova (baza) indukcije, a implikacija ![]() indukcijski korak, dok se formula
indukcijski korak, dok se formula ![]() u ovoj implikaciji naziva indukcijska hipoteza (pretpostavka).
u ovoj implikaciji naziva indukcijska hipoteza (pretpostavka).
Primena metoda matematičke indukcije u pokušaju dokazivanja nekog tvrđenja
podrazumeva dokaz baze indukcije i induktivnog koraka, jer su to dva nezavisna
tvrđenja tj. ni jedno ne proizilazi iz onog drugog. Ako nešto od ova dva
uslova nije tačno, onda je i ![]() netačno.
netačno.
Ako se ne provere oba uslova, mogu nastati greške, npr. ![]() je tačno za
je tačno za ![]() ,
ali ne važi ni za jedan drugi prirodan broj jer
,
ali ne važi ni za jedan drugi prirodan broj jer ![]() očigledno nije tačna. Češća greška je da se ne dokaže baza, a dokaže se
samo indukcijski korak, npr.
očigledno nije tačna. Češća greška je da se ne dokaže baza, a dokaže se
samo indukcijski korak, npr. ![]() očigledno ne važi za
očigledno ne važi za ![]() ali implikacija
ali implikacija ![]() važi jer iz
važi jer iz ![]() dodavanjem jedinice levoj i desnoj strani dobijamo
dodavanjem jedinice levoj i desnoj strani dobijamo ![]() .
.
Princip matematičke indukcije se suštinski razlikuje od tzv. empirijske
indukcije koja se sastoji u posmatranju ili eksperimentisanju, najčešće
u prirodnim naukama. Ovakvo rasuđivanje ima svoju primenu i u matematici
jer je pomoću njega otkriveno, a kasnije dokazano više važnih stavova,
ali ponekad može dovesti i do formulacija tvrđenja za koje se pokazuje
da su pogrešna.
Tako je npr. čuveni francuski matematičar Pjer Ferma posmatrajući brojeve
![]() ,
koji su prosti za
,
koji su prosti za ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
izveo pretpostavku da su svi brojevoi oblika
,
izveo pretpostavku da su svi brojevoi oblika ![]() prosti. Kasnije je utvrđeno da je broj
prosti. Kasnije je utvrđeno da je broj ![]() deljiv sa 641, a isto tako da su i
deljiv sa 641, a isto tako da su i ![]() složeni brojevi za
složeni brojevi za ![]() .
.
Empirijskom indukcijom, kao što je već rečeno, mogu se naslutiti neke
fornule (jednakosti, nejednakosti i slično) koje zavise od prirodnog broja
![]() ,
a metod matematičke indukcije omogućuje da u mnogim slučajevima utvrdimo
da li je postavljena hipoteza tačna ili nije.
,
a metod matematičke indukcije omogućuje da u mnogim slučajevima utvrdimo
da li je postavljena hipoteza tačna ili nije.
Princip matematičke indukcije nije dokazan već detaljno objašnjen. Izvešćemo sada jedan dokaz principa matematičke indukcije, dokazujući uz put jedno pomoćno svojstvo prirodnih brojeva, tzv. princip najmanjeg broja:
Teorema 1
Svaki neprazan podskup A skupa N ima najmanji element.
Dokaz:
Pretpostavimo da je A neprazan i da nema najmanji element. Neka
je C skup svih prirodnih brojeva koji su manji od svakog elementa
skupa A, tj. ![]() .
Dokazaćemo primenom aksiome indukcije da je C=N.
.
Dokazaćemo primenom aksiome indukcije da je C=N.
Prvi uslov ![]() sledi iz pretpostavke da A nema najmanji element i da je 1 najmanji
u skupu N.
sledi iz pretpostavke da A nema najmanji element i da je 1 najmanji
u skupu N.
Pretpostavimo da je ![]() .
Treba da pokažemo da je
.
Treba da pokažemo da je ![]() .
U suprotnom
.
U suprotnom ![]() bi bio najmanji u A, što protivreči pretpostavci da u A
ne postoji najmanji element.
bi bio najmanji u A, što protivreči pretpostavci da u A
ne postoji najmanji element.
Znači ![]() .
Odavde sledi da je A prazan skup što je u kontradikciji sa pretpostavkom.
■
.
Odavde sledi da je A prazan skup što je u kontradikciji sa pretpostavkom.
■
Vratimo se sada na dokaz principa matematičke indukcije.
Pretpostavimo da su ![]() tvrđenja za koja važi
tvrđenja za koja važi
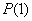 tačno,
tačno,- za svaki
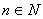 ,
iz tačnosti
,
iz tačnosti 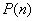 sledi tačnost
sledi tačnost 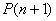 .
.
Dokažimo da su sva tvrđenja ![]() tačna. Pretpostavimo suprotno, tj. da postoji neko tvrđenje u ovom nizu
koje nije tačno. To znači da je skup svih prirodnih brojeva n
takvih da je
tačna. Pretpostavimo suprotno, tj. da postoji neko tvrđenje u ovom nizu
koje nije tačno. To znači da je skup svih prirodnih brojeva n
takvih da je ![]() netačno neprazan, pa na osnovu principa najmanjeg broja postoji najmanji
prirodan broj m takav da je
netačno neprazan, pa na osnovu principa najmanjeg broja postoji najmanji
prirodan broj m takav da je ![]() netačno. Na osnovu a) zaključujemo da je
netačno. Na osnovu a) zaključujemo da je ![]() .
Međutim kako je
.
Međutim kako je ![]() ,
tvrđenje
,
tvrđenje ![]() mora biti tačno.
mora biti tačno.
Dakle ![]() je netačno, dok je
je netačno, dok je ![]() tačno, što je u suprotnosti sa b). Time je dokaz završen.
tačno, što je u suprotnosti sa b). Time je dokaz završen.
Drugi oblici primene matematičke indukcije
Regresivna indukcija
Istinitost nekog metoda ![]() ,
za svako
,
za svako ![]() po metodu regresivne indukcije sledi iz:
po metodu regresivne indukcije sledi iz:
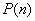 je tačno za beskonačno mnogo prirodnih brojeva
je tačno za beskonačno mnogo prirodnih brojeva 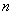
- za sve prirodne brojeve
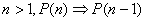 je tačan iskaz.
je tačan iskaz.
Primer 1.
Dokazati da za sve prirodne brojeve ![]() i sve nenegativne realne brojeve
i sve nenegativne realne brojeve ![]() važi nejednakost aritmetičke i geometrijske sredine
važi nejednakost aritmetičke i geometrijske sredine
![]()
![]() .
.
1. Najpre matematičkom indukcijom po k dokazujemo da tvrđenje važi za
sve prirodne brojeve oblika ![]()
![]() .
.
1.’ Za ![]() (
(![]() )
nejednakost
)
nejednakost ![]() je ekvivlentna sa
je ekvivlentna sa ![]() .
.
2.’ Pretpostavimo da tvrđenje važi za ![]() .
Tada je
.
Tada je
![]()
![]() .
.
Zaključujemo da nejednakost važi za sve ![]() .
.
2. Pretpostavimo sada da je nejednakost tačna za neki prirodan broj ![]() i izaberimo
i izaberimo ![]() .
Tada je
.
Tada je
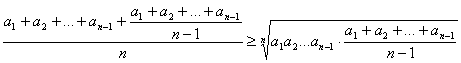 , odavde se dobija
, odavde se dobija ![]() ,
tj.
,
tj.
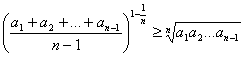 ,
pa je
,
pa je
![]() .
.
Ovde smo dokazali da nejednakost važi i za ![]() ,
pa dalje zaključujemo da važi za sve prirodne brojeve.
,
pa dalje zaključujemo da važi za sve prirodne brojeve.
Primetimo da u datoj nejednakosti (za ![]() )
jednaskost važi ako i samo ako je
)
jednaskost važi ako i samo ako je ![]() .
.
Rekurentna indukcija
Postoje tvrđenja koja se dokazuju metodom matematičćke indukcije, ali
je pri dokazivanju indukcijskog koraka praktičnije pretpostaviti ![]() i dokazati
i dokazati ![]() .
Drugačije rečeno, ne čini se korak sa
.
Drugačije rečeno, ne čini se korak sa ![]() ka
ka ![]() ,
već sa nekoliko
,
već sa nekoliko ![]() koji prethode
koji prethode ![]() ka
ka ![]() .
Znači ako indukcijski korak ima
.
Znači ako indukcijski korak ima ![]() pretpostavki ovaj princip se može zapisati:
pretpostavki ovaj princip se može zapisati:
![]() .
.
Ovu formulu označavamo ![]()
![]()
Ovaj princip matematičke indukcije je ekvivalentan osnovnom principu.
Primer 1.
Ako je ![]() i
i ![]() ,
dokazati da je
,
dokazati da je ![]()
![]() .
.
1. ![]() ,
,
![]() ,
pa je tvrđenje tačno za
,
pa je tvrđenje tačno za ![]() i za
i za ![]() .
.
2. važi za ![]() i
i ![]()
![]()
![]()
![]()
Pa važi i za ![]() .
.
Sledi da za svaki prirodan broj važi tvrđenje.
Transfinitna indukcija
Kod pojedinih tvrđenja o prirodnim brojevima za dokaz da važi ![]() treba dokazati sledeće:
treba dokazati sledeće:
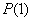 je tačan iskaz;
je tačan iskaz;- za sve
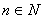 ,
ako su
,
ako su 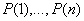 tačni iskazi, onda je i
tačni iskazi, onda je i 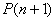 tačan iskaz.
tačan iskaz.
Ova vrsta indukcije se zapisuje kao:
![]() .
.
Primer 1.
Ako je ![]() i za
i za ![]() ,
,
![]() ,
tada je za sve prirodne brojeve
,
tada je za sve prirodne brojeve ![]() ispunjeno
ispunjeno ![]() .
.
1. ![]()
![]()
2. Pretpostavimo da je ![]() i
i ![]() .
Tada je:
.
Tada je:
![]() .
.
Primer 2.
Dokazati da je svaki prirodan broj ![]() ili prost ili je proizvod prostih brojeva.
ili prost ili je proizvod prostih brojeva.
1. Za ![]() broj 2 je prost, pa je tvrđenje tačno.
broj 2 je prost, pa je tvrđenje tačno.
2. Neka je ![]() prirodan broj. Pretpostavimo da tvrđenje važi za sve
prirodan broj. Pretpostavimo da tvrđenje važi za sve ![]() .
Broj
.
Broj ![]() je prost, pa tvrđenje važi. Ako je složen
je prost, pa tvrđenje važi. Ako je složen ![]() se
može napisati u obliku
se
može napisati u obliku ![]() ,
gde su
,
gde su ![]() i
i ![]() prirodni brojevi manji od
prirodni brojevi manji od ![]() .
Međutim, za
.
Međutim, za ![]() i
i ![]() važi indukcijska pretpostavka, pa su oni prosti ili proizvod prostih brojevai
i u tom slučaju je i
važi indukcijska pretpostavka, pa su oni prosti ili proizvod prostih brojevai
i u tom slučaju je i ![]() proizvod prostih brojeva.
proizvod prostih brojeva.
Indukcija „sa skokom“
Ponekad nije lako, ili pak nije moguće izvesti induktivni korak ![]() ,
ali smo u stanju da izvedemo
,
ali smo u stanju da izvedemo ![]() .
Tada se baza indukcije dokazuje za
.
Tada se baza indukcije dokazuje za ![]() .
Znači
.
Znači ![]() ako:
ako:
1. ![]() je tačno,
je tačno,
2. ![]() je tačan iskaz za sve
je tačan iskaz za sve ![]() .
.
Tačnost ovog principa se ogleda u tome da primenjujući induktivni korak
redom na brojeve ![]() ,...
za koje tvrđenje važi zbog 1. dobijamo da tvrđenje važi i za
,...
za koje tvrđenje važi zbog 1. dobijamo da tvrđenje važi i za ![]() .
Dalje primenjujući 2. na
.
Dalje primenjujući 2. na ![]() ,
dobijamo da tvrđenje važi i za
,
dobijamo da tvrđenje važi i za ![]() ,
itd. Dobijamo da tada
,
itd. Dobijamo da tada ![]() važi za sve prirodne brojeve.
važi za sve prirodne brojeve.
Primer 1
Dokazati da se svaka mreža od ![]() gradova može povezati jednosmernim autobuskim linijama, takvim da se iz
svakog grada može stići u svaki drugi sa najviše jednim presedanjem.
gradova može povezati jednosmernim autobuskim linijama, takvim da se iz
svakog grada može stići u svaki drugi sa najviše jednim presedanjem.
Dokažimo najpre tvrđenje za ![]() i
i ![]() .
.
Za ![]() gradove treba povezati Za
gradove treba povezati Za ![]() šema je sledeća:
šema je sledeća:
kao na slici:
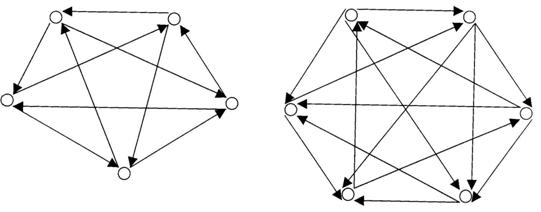
a) b)
sl. 1.
Pretpostavimo sada da za neko ![]() postoji mreža autobuskih linija koje zadovoljavaju uslove zadatka. Uzmimo
sada
postoji mreža autobuskih linija koje zadovoljavaju uslove zadatka. Uzmimo
sada ![]() grada. Izdvojimo iz tog skupa bilo koja dva grada A i B. Preostalih
grada. Izdvojimo iz tog skupa bilo koja dva grada A i B. Preostalih ![]() gradova možemo povezati na željeni način, po pretpostavci. Dodavši gradove
A i B, mrežu jednosmernih linija dopunjujemo na sledeći način: Napravimo
liniju od A ka B, zatim, jednosmerne linije od B do svakog od preostalih
gradova možemo povezati na željeni način, po pretpostavci. Dodavši gradove
A i B, mrežu jednosmernih linija dopunjujemo na sledeći način: Napravimo
liniju od A ka B, zatim, jednosmerne linije od B do svakog od preostalih
![]() gradova,
i najzad linije do svakog od preostalih
gradova,
i najzad linije do svakog od preostalih ![]() gradova do A. Takva mreža zaista zadovoljava uslove zadatka jer: od A
se može doći do B direktnom linijom, a u bilo koji od preostalih
gradova do A. Takva mreža zaista zadovoljava uslove zadatka jer: od A
se može doći do B direktnom linijom, a u bilo koji od preostalih ![]() gradova preko B; iz B se može stići u bilo koji grad direktnom linijom,
osim u grad A, u koji se može stići preko bilo kog od preostalih
gradova preko B; iz B se može stići u bilo koji grad direktnom linijom,
osim u grad A, u koji se može stići preko bilo kog od preostalih ![]() gradova; iz bilo kog grada iz skupa preostalih
gradova; iz bilo kog grada iz skupa preostalih ![]() gradova može se stići do A direktnom linijom, do B sa jednim presedanjem
preko grada A, a oni po pretpostavci poseduju mrežu autobuskih linija
po kojoj se iz svakog grada iz tog skupa može stići u bilo koji drugi
sa najviše jednim presedanjem.
gradova može se stići do A direktnom linijom, do B sa jednim presedanjem
preko grada A, a oni po pretpostavci poseduju mrežu autobuskih linija
po kojoj se iz svakog grada iz tog skupa može stići u bilo koji drugi
sa najviše jednim presedanjem.
Zaključujemo da za bilo koji broj gradova ![]() postoji tražena mreža jednosmernih autobuskih linija.
postoji tražena mreža jednosmernih autobuskih linija.
Primena indukcije u geometriji
Izračunavanje pomoću indukcije
Najprirodniji način upotrebe indukcije u geometriji ustvari onaj najbliži upotrebi indukcije u teoriji brojeva u algebri, a to je rešavanje računskih problema u geometriji.
Primer: Dokažimo da je zbir unutrašnjih uglova u konveksnom
n-touglu jednak ![]() .
.
- n=3
Zbir unutrašnjih uglova u trouglu je ![]() .
(S3=180
.
(S3=180![]() )
.
)
.
Zbir uglova u četvorouglu je 360![]() (svaki
četvorougao se može podeliti na dva trougla (sl. 2a)).
(svaki
četvorougao se može podeliti na dva trougla (sl. 2a)).
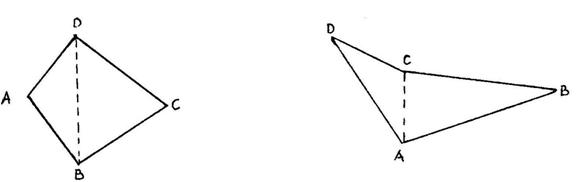
a) b)
sl. 2.
- Pretpostavimo da važi da je zbir unutrašnjih uglova bilo kog m-tougla
(m<n) jednak
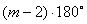 .Posmatrajmo
sada n-tougao A1,A2,...,An.
.Posmatrajmo
sada n-tougao A1,A2,...,An.
Pre svega treba dokazati da se svaki poligon može podeliti dijagonalom
na dva poligona sa manjim brojem strana (za konveksni poligon možemo uzeti
bilo koju dijagonalu). Neka su A, B, C bilo koja tri susedna temena poligona,
a kroz teme B povlačimo sve moguće krake popunjavajući unutrašnjost ugla
![]() .
Postoje dva moguća slučaja:
.
Postoje dva moguća slučaja:
- Svi zraci presecaju jednu istu stranu poligona (sl. 3a)). U ovom slučaju dijagonala AC deli n-tougao na (n-1)-ugaonik i trougao.
- Ne seku svi zraci jednu istu stranu poligona (sl. 3b)). U ovom slučaju jedan od zraka će proći kroz određeno teme M tog poligona, a dijagonala BM će podeliti poligon na dva poligona, svaki sa manje strane nego prvobitni poligon.
a) b)
sl. 3.
Vratimo se sada dokazu glavnog problema. Uzmimo dijagonalu A1Ak u n-touglu
A1A2...An koji deli n-tougao na k-tougao A1A2...Ak i (n-k+2)-tougao A1AkAk+1...An.
Po pretpostavci zbir uglova u k-touglu i (n-k+2)-touglu jednak je redom
(k-2)![]() i
i ![]() .
Odatle proizilazi da je zbir uglova u n-touglu jednak
.
Odatle proizilazi da je zbir uglova u n-touglu jednak ![]() .
.
Dakle ova pretpostavka važi za svako n![]() .
.
Dokazivanje pomoću indukcije
Matematička indukcija se takođe može koristiti u dokazima nekih teorema
u geometriji. Prethodni primer se takođe može posmatrati kao dokaz pomoću
indukcuje (teorema o zbiru unutrašnjih uglova u n-touglu).
Sada ćemo videti još nekoliko primera dokaza pomoću indukcije.
Primer1: ![]()
Dato je n proizvoljnih kvadrata.Dokazati da je moguće iseći ih na takav
način, da se od svih isečenih delova može sastaviti novi kvadrat.
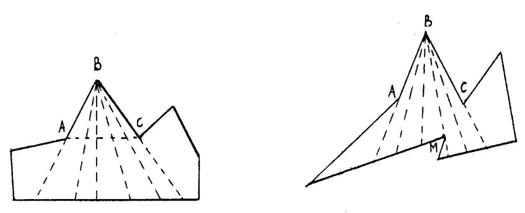
1. Za n=1 ne treba dokaz. Dokažimo da pretpostavka važi za n=2.
Označimo dužine stranica kvadrata ABCD sa x i A1B1C1D1 sa y i neka je
x![]() y.
Na stranicama kvadrata ABCD (sl. 4a)), označimo tačke M, N, P, Q.tako
da je AM=BN=CP=DQ=
y.
Na stranicama kvadrata ABCD (sl. 4a)), označimo tačke M, N, P, Q.tako
da je AM=BN=CP=DQ=![]() i isecimo kvadrat po dužima MP i NQ, koje se seku pod pravim uglom (što
se može lako dokazati) u tački O i tako dele kvadrat ABCD na četiri jednaka
dela. Spajanjem ovih delova sa kvadratom A1B1C1D1 u novu figuru kao što
je prikazano na slici 4b). Figura koju smo dobili takođe je kvadrat, pošto
su uglovi u tačkama M’, N’, P’, Q’ suplementni,
uglovi A’, B’, C’, D’ su pravi i A’B’=B’C’=
C’D’=D’A’.
i isecimo kvadrat po dužima MP i NQ, koje se seku pod pravim uglom (što
se može lako dokazati) u tački O i tako dele kvadrat ABCD na četiri jednaka
dela. Spajanjem ovih delova sa kvadratom A1B1C1D1 u novu figuru kao što
je prikazano na slici 4b). Figura koju smo dobili takođe je kvadrat, pošto
su uglovi u tačkama M’, N’, P’, Q’ suplementni,
uglovi A’, B’, C’, D’ su pravi i A’B’=B’C’=
C’D’=D’A’.
a) b)
sl. 4.
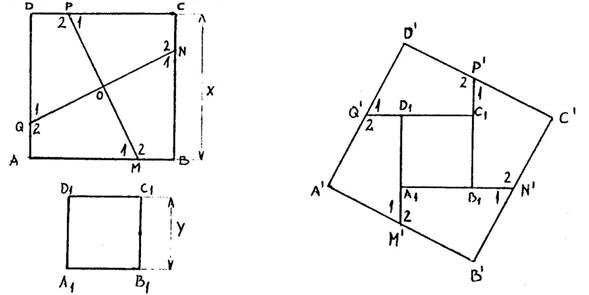
2. Pretpostavimo da je moguće od n kvadrata sečenjem dobiti jedan nov.
Treba dokazati da to važi za n+1 kvadrat (K1, K2, ..., Kn+1).
Uzmimo bilo koja dva kvadrata od datih n+1, recimo Kn i Kn+1. Kako je
pokazano u delu 1. , sečenjem i spajanjem delova ova dva kvadrata dobijamo
novi kvadrat K’. Tada je po pretpostavci moguće sečenjem kvadrata
K1, K2, ..., Kn-1, K’ dobiti jedan nov, što je i trebalo dokazati.
Ovim smo dokazali da se od bilo koliko kvadrata sečenjem i spajanjem
može dobiti jedan veliki kvadrat.
a)
b)
sl. 5.
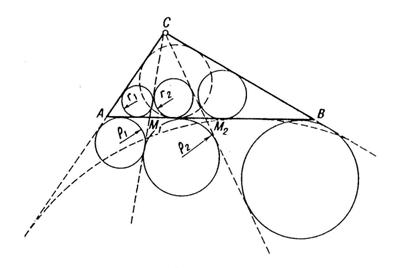
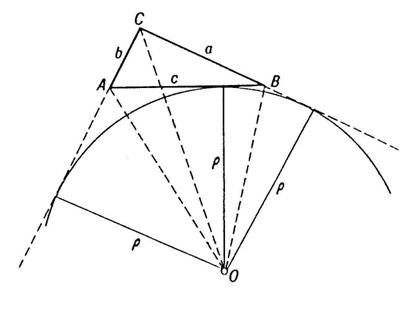
Primer 2:
Dat je trougao ABC sa n-1 pravih CM1, CM2, ..., CMn-1, povučenim kroz
teme C, koje dele trougao na n manjih trouglova ACM1, M1CM2, ..., M1CB.Označimo
sa r1, r2, ..., rn i q1, q2, ..., qn redom poluprečnike upisanih i spolja
upisanih krugova (svi spolja upisani krugovi su upisani u okviru ugla
C (sl. 5a)) i neka su r i q poluprečnici upisanog i spolja upisanog kruga
trougla ABC. Dokazati:![]() .
Označimo sa P površinu trougla ABC, sa s poluobim; tada je
.
Označimo sa P površinu trougla ABC, sa s poluobim; tada je ![]() .
Sa druge strane, ako je O centar spolja upisanog kruga ovog trougla (sl.
5b)), tada je
.
Sa druge strane, ako je O centar spolja upisanog kruga ovog trougla (sl.
5b)), tada je
![]() .
.
Pošto je ![]() ,
dobijamo
,
dobijamo ![]() .
.
Pomoću trigonometrijskih formula 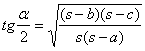 i
i 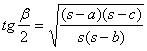 dobijamo
dobijamo
(1)![]() .
.
Vratimo se sada dokazu teoreme.
1.Dokažimo da teorema važi za ![]() .
U ovom slučaju trougao ABC je podeljen pravom CM na dva manja trougla
ACM i CMB.
.
U ovom slučaju trougao ABC je podeljen pravom CM na dva manja trougla
ACM i CMB.
Pomoću formule (1) dobijamo:
![]()
![]() .
.
2.Pretpostavimo da smo dokazali da teorema važi za n-1 pravu i da imamo
n pravih![]() koje dele trougao ABC na n+1 manjih trouglova
koje dele trougao ABC na n+1 manjih trouglova ![]() .Posmatrajmo
dva od tih trouglova, recimo
.Posmatrajmo
dva od tih trouglova, recimo ![]() i
i ![]() .
Kao što smo videli u 1.
.
Kao što smo videli u 1. ![]() ,
gde su
,
gde su ![]() i
i ![]() poluprečnici upisanog i spolja upisanog kruga trougla
poluprečnici upisanog i spolja upisanog kruga trougla ![]() .
Pošto za n trouglova
.
Pošto za n trouglova ![]() .
Važi:
.
Važi:
![]() .
.
Odavde sledi da je ![]() . Ovim smo dokazali da tvrđenje važi za svako n.
. Ovim smo dokazali da tvrđenje važi za svako n.
KONSTRUKCUJA POMOĆU INDUKCIJE
Metod matematičke indukcije se može koristiti za rešavanje konstrukcijskih problema pod uslovom da kao argument u problemu figuriše proizviljan prirodan broj (na primer problem konstrukcije n-tougla). Na sledećem primeru ćemo videti način na koji se koristi indukcija u konstrukciji.
Primer: Dato je 2n+1 tačaka. Konstruisati (2n+1)-ugaonik, kod koga su date tačke središta stranica.
1. Za n=1 problem se svodi na konstrukciju trougla. Ovaj problem se lako rešava. Povučemo pravu kroz svaku tačku, tako da ona bude paralelna pravoj koja prolazi kroz druge dve tačke.
2. Pretpostavimo da možemo konstruisati (2n-1)-ugaonik ako su data središta
njegovih stranica i neka je dato 2n+1 tačaka ![]() ,
tako da su one središta traženog (2n+1)-ugaonika
,
tako da su one središta traženog (2n+1)-ugaonika ![]() .
.
Posmatrajmo četvorougao ![]() (sl. 6). Tačke
(sl. 6). Tačke ![]() služe kao središta stranica
služe kao središta stranica ![]() i neka je
i neka je ![]() središte stranice
središte stranice ![]() .
Četvorougaonik
.
Četvorougaonik ![]() je ustvari paralelogram (da bi to dokazali dovoljno je povući dijagonalu
je ustvari paralelogram (da bi to dokazali dovoljno je povući dijagonalu
![]() i onda posmatrati trouglove
i onda posmatrati trouglove ![]() i
i ![]() kod kojih su
kod kojih su ![]() i
i ![]() redom srednje linije). Pošto su tačke
redom srednje linije). Pošto su tačke ![]() zadate uslovom zadatka, tačku
zadate uslovom zadatka, tačku ![]() je lako odrediti (kao četvrto teme paralelograma
je lako odrediti (kao četvrto teme paralelograma ![]() ).
Tačke
).
Tačke ![]() su središta stranica (2n-1)-ugaonika
su središta stranica (2n-1)-ugaonika ![]() ,
koji se po pretpostavci može konstruisati. Sada treba odrediti još samo
temena
,
koji se po pretpostavci može konstruisati. Sada treba odrediti još samo
temena ![]() i
i ![]() ,
što je lako uraditi pošto su temena
,
što je lako uraditi pošto su temena ![]() i
i ![]() već određena, a središta duži
već određena, a središta duži ![]() i
i ![]() (tj. tačke
(tj. tačke ![]() i
i ![]() )
zadate uslovom zadatka.
)
zadate uslovom zadatka.
DEFINISANJE POMOĆU INDUKCIJE
Matematička indukcija ima primenu i u definisanju u geometriji.
Primer: Definicija središta duži i težišta n-tougla
1. Središte duži ćemo nazvati težištem.(sl. 7a))
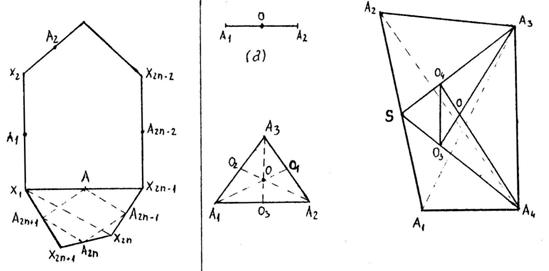
a) b)
sl. 6.
sl. 7.
Težišne duži trougla ![]() onda se mogu definisati kao duži koje spajaju temena trougla sa težištima
suprotnih stranica. Kao što znamo težišne duži u trouglu seku se u jednoj
tački koja deli svaku težišnu duž u odnosu 2:1. Ta tačka naziva se težištem
trougla.
onda se mogu definisati kao duži koje spajaju temena trougla sa težištima
suprotnih stranica. Kao što znamo težišne duži u trouglu seku se u jednoj
tački koja deli svaku težišnu duž u odnosu 2:1. Ta tačka naziva se težištem
trougla.
Definišimo sada težišne duži četvorougla ![]() koje spajaju svako od temena
koje spajaju svako od temena ![]() redom sa težištima (
redom sa težištima (![]() )
trouglova koje sačinjavaju ostala tri temena. Dokažimo sada da se sve
težišne duži seku u jednoj tački koja ih deli u odnosu 3:1. Neka je
)
trouglova koje sačinjavaju ostala tri temena. Dokažimo sada da se sve
težišne duži seku u jednoj tački koja ih deli u odnosu 3:1. Neka je ![]() težište stranice
težište stranice![]() i neka su
i neka su ![]() i
i ![]() težišta trouglova
težišta trouglova ![]() i
i ![]() redom. Neka je
redom. Neka je ![]() tačka preseka težišnih duži
tačka preseka težišnih duži ![]() i
i
![]() četvorougla
četvorougla ![]() .
Pošto su
.
Pošto su ![]() i
i ![]() težišne duži trouglova
težišne duži trouglova ![]() i
i ![]() možemo reći:
možemo reći:
![]() i
i ![]()
![]()
![]() .
.
Odatle sledi ![]() i
i ![]() .
.
Iz sličnosti trouglova ![]() i
i ![]() imamo da je
imamo da je ![]() .
Znači svake dve susedne težišne duži seku se u odnosu 3:1. Odatle sledi
da se sve težišne duži četvorougla seku u jednoj tački koja ih deli u
odnosu 3:1. Ta tačka se zove težištem četvorougla.
.
Znači svake dve susedne težišne duži seku se u odnosu 3:1. Odatle sledi
da se sve težišne duži četvorougla seku u jednoj tački koja ih deli u
odnosu 3:1. Ta tačka se zove težištem četvorougla.
2. Pretpostavimo da smo za svako ![]() definisali težišne duži k-tougla kao duži koje spajaju temena tog k-tougla
sa težištem (k-1)-tougla, koji sačinjavaju preostalih
definisali težišne duži k-tougla kao duži koje spajaju temena tog k-tougla
sa težištem (k-1)-tougla, koji sačinjavaju preostalih ![]() temena i da smo za svako
temena i da smo za svako ![]() definisali težište k-tougla kao presečnu tačku njegovih težišnih duži.
Takođe ćemo pretpostaviti da za svako
definisali težište k-tougla kao presečnu tačku njegovih težišnih duži.
Takođe ćemo pretpostaviti da za svako ![]() težište deli težišne duži k-tougla u odnosu (k-1):1.
težište deli težišne duži k-tougla u odnosu (k-1):1.
Definišimo sada težišne duži n-tougla kao duži koje spajaju teme sa težištem
(n-1)-tougla .Dokažimo sada da se sve težišne duži seku u jednoj tački
koja ih deli u odnosu (n-1):1. Neka je ![]() težište (n-2)-tougla
težište (n-2)-tougla ![]() .
Tada su duži
.
Tada su duži ![]() i
i
![]() ustvari težišne duži (n-1)-touglova
ustvari težišne duži (n-1)-touglova ![]() i
i ![]() (sl.
8). Ako su
(sl.
8). Ako su ![]() i
i ![]() težišta
ovih mnogouglova, onda po induktivnoj pretpostavci važi:
težišta
ovih mnogouglova, onda po induktivnoj pretpostavci važi:
![]() .
.
Iz ovoga dobijamo ![]() i
i ![]() .
Označimo sada presečnu tačku težišnih duži
.
Označimo sada presečnu tačku težišnih duži ![]() i
i ![]() n-tougla
n-tougla ![]() sa
sa ![]() .
Iz sličnosti trouglova
.
Iz sličnosti trouglova ![]() i
i ![]() dobijamo:
dobijamo:
![]() .
.
Pošto se svake dve susedne duži n-tougla seku u tački koja ih deli u odnosu
(![]() ):1,
sledi da se sve težišne duži seku u istoj tački. Tu tačku nazivamo težištem
n-tougla.
):1,
sledi da se sve težišne duži seku u istoj tački. Tu tačku nazivamo težištem
n-tougla.
Zakljužujemo da naša definicija težišnih duži i težišta n-tougla važi
za svako n.
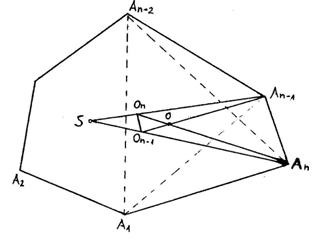
sl. 8.
ZAKLJUČAK
Matematička indukcija je veoma značajna metoda koja zbog svoje matematičke
strogosti uvek dovodi do tačnih zaključaka. Usavršavajući se i uobličavajući
kroz vekove matematička indukcija je tek krajem devetnaestog veka nakon
definisanja skupa prirodnih brojeva preko Peanovih aksioma kompletno formirana
i jasno definisana.
Teško je i zamisliti šta bi matematika bila bez matematičke indukcije.
Počevši od najjednostavnijih elementarnih problema vezanih za prirodne
brojeve pa do složenih problema iz teorije matematike mnogi se mogu svesti
na matematičku indukciju.
Istorijat matematičke indukcije
Teško je sa sigurnošću utvrditi ko je prvi precizno iskazao princip matematičke
indukcije. Tragovi dokazivanja pomoću potpune indukcije mogu se naći u
spisima Zenona, Platona i Euklida.
A.Ostrowski navodi da je Levi Ben Gerson (1288-1344) 1321. godine prvi
precizno iskazao princip matematičke indukcije.
Kao pronalazači matematičke indukcije navode se takođe i F. Maurolico
(1494-1575), J. Bornouli(1645-1705), ali prema novijim proučavanjima izgleda
da nejviše zasluga za jasno formulisanje principa matematičke indukcije
ima B. Pascal (1623-1662). Kao što se vidi princip matematičke indukcije
poznat je ljudime mnogo vekova unazad.
LITERATURA
1.D.S.Mitrinović:Metod matematičke indukcije
2.L.I.Golovina and I.M.Yaglom:Induction in geometry
3.D.S.Mitrinović, D.S.Mihailović, P.M.Vasić:Linearna algebra, polinomi, analitička geometrija
4.M.Božić, S.Vulić:Matematička logika sa elementima opšte logike
5.D.Lopandić:Zbirka zadataka iz osnova geometrije
preuzmi
seminarski rad u wordu » » »
