HERONOVA FORMULA

Površina nejednakostraničnog trougla

Formula za izračunavanje površine nejednakostraničnog trougla kojem su poznate dužine sve tri stranice:

 ∆=

poznata je pod imenom Heronova formula.

U Metrici (knjiga I) Heron razmatra problem izračunavanja površine trougla stranica poznatih dužina i nudi dva metoda za rešavanje problema:

I metod:
 
Ovaj metod je baziran na 12. i 13. stavu II knjige Elemenata   :
stav 12: U svakom tupouglom trouglu kvadrat na strani naspram tupog ugla je veći od zbira kvadrata na stranama koje obrazuju tup ugao za dvostruki pravougaonik obuhvaćen jednom stranom tupog ugla(onom na čije produženje pada spuštena normala) i rastojanjem te normale od temena tupog ugla.
stav 13: U svakom oštrouglom trouglu kvadrat na strani naspram oštrog ugla je manji od zbira kvadrata na stranama koje obrazuju oštar ugao za dvostruki pravougaonik obuhvaćen jednom stranom oštrog ugla(onom na koju je spuštena normala) i rastojanjem te normale od temena oštrog ugla.

Vratimo se sada samom metodu:
˝ Neka su a,b i c stranice trougla ∆ABC naspramne temenima A,B i C, respektivno. Za bilo koji ugao (uzmimo onaj kod temena C) važi :

Ugao kod C je ako važi:

 c2  a2+b2  oštar 
  prav
  tup

Metod se zasniva na određivanju, prvo segmenata na koje je bilo koja stranica podeljena normalom iz naspramnog temena, a zatim dužinom normale.
U slučaju trougla sa oštrim uglom kod C (tupim uglom kod C, respektivno) važi:

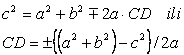
Odakle nalazimo AD () potrebnu za izračunavanje površine ().˝

II metod :
Neka je ∆ABC dati trougao i neka je data svaka od stranica AB, BC, CA.  U trougao upišimo krug sa centrom O i dodirne tačke sa stranicama AB, BC i CA obeležimo redom sa F, D i E. Konstruišimo duži AO, BO, CO, DO, EO i FO spajanjem odgovarajućih tačaka.
Tada važi:
BC∙OD = 2∆BOC,
CA∙OE = 2∆COA,
AB∙OF = 2∆AOB

gde ∆ označava površinu trougla.

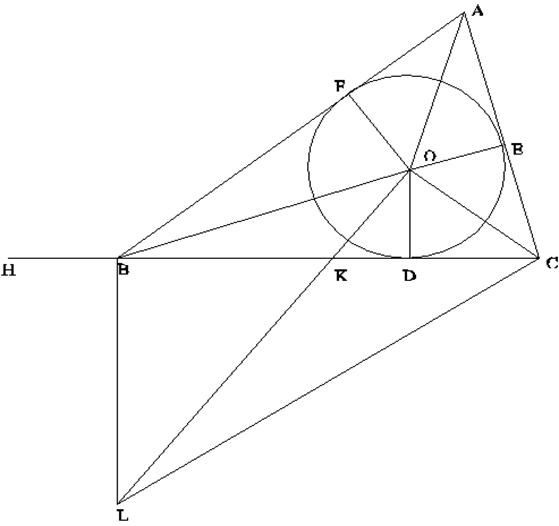
Slika 1

Sabiranjem sve tri jednakosti dobijamo :

 p∙OD= 2∆ABC , gde je p poluobim trougla.

Produžimo stranicu CB do tačke H takve da važi jednakost BH=AF.
Pošto je:

 AE=AF, BF=BD i CE=CD, to je CH=p/2=s.

Odatle sledi: CH∙OD= ∆ABC
Kvadriranjem poslednje jednakosti dobijamo CH2∙OD2 =(∆ABC)2   (*)

Konstruišimo sada duž OL takvu da važi COL=R i OL seče BC u tački K i duž BL takvu da CBL=R i OL i BL se seku u L.
Konstruišimo i duž CL.
Pošto su uglovi COL i CBL pravi, COBL je četvorougao upisan u krug (tetivni četvorougao), pa važi   COB + CLB=2R. 
Ali važi i
COB + AOF=2R
(jer AO,BO i CO polove uglove oko O i uglovi COB, AOF su zajedno jednaki uglovima AOC, BOF, dok je zbir sva četiri ugla jednak 4R)

Kao posledicu dobijamo: AOF=CLB

Odatle sledi da su pravougli trouglovi ∆AOF i ∆CLB slični, pa važe sledeći odnosi:
 BC:BL=AF:FO
=BH:OD
tj . BC:BH=BL:OD
I trouglovi ∆ODK i ∆LBK su slični. Dakle:
BL:OD=BK:KD
tj . BC:BH=BK:KD
Na osnovu prethodnog dobijamo:
 CH:HB=BD:DK

Sledi da CH2: (CH∙HB)=(BD∙DC) : (CD∙DK)
 =(BD∙DC) : OD2 , jer je COK=R

Pošto je: ∆ABC² = CH2∙OD² (*) i CH²∙OD²=CH∙HB∙BD∙DC , površina trougla je zadata formulom:

 ∆ABC² =s(s-a)(s-b)(s-c)

Pomoću Heronove formule može se dokazati Pitagorina teorema!
Dokaz: Koristićemo standardne oznake:
 a,b,c za dužine stranica
 p za poluobim trougla, i
S za površinu trougla .

Heronova formula daje jednakost:

S2=p(p-a)(p-b)(p-c)

U pravouglom* trouglu sa hipotenuzom c, važi S=ab/2.
Modifikujmo desnu stranu jednakosti koristeći sledeće:

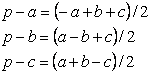
Primenom elementarne algebre dobija se jednakost:

*posmatramo samo ovu vrstu trouglova jer dokazujemo Pitagorinu teoremu.

Daljim sređivanjem ovog izraza dobija se:

tj. 

Najzad:

Napomena: za četvorougao sa stranicama a, b, c, d upisan u krug, postoji generalizacija Heronove formule, koju je otkrio Brahmagupta. U ovom slučaju, poluobim je definisan sa p=(a+b+c+d)/2 , pa važi formula

Pošto se svaki trougao može upisati u krug, možemo zahtevati da jedna stranica četvorougla (recimo d) bude jednaka 0. Tada se prethodna formula svodi na Heronovu.

Ipak, Heronova formula se danas dokazuje na mnogo jednostavniji način. Može se koristiti kosinusna teorema ili sličnost trouglova, kao u dokazu koji sledi:

Neka je dat trougao ABC sa stranicama:

 BC=a,
CA=b i
AB=c

Neka je h visina trougla spuštena iz temena A na stranicu BC i A' podnožje te visine. Tačka A' deli stranicu BC na dva dela. Deo BA' označimo sa x. Tada je A'C=a-x.

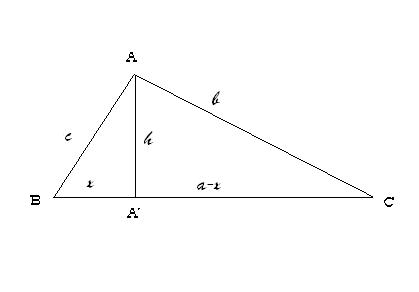
Posmatrajmo prvo trougao ABA' ! To je pravougli trougao (), pa primenom Pitagorine teoreme dobijamo za dokaz važnu jednakost:

   (1)
Primenom Pitagorine teoreme na trougao AA'C, dobijamo drugu važnu jednakost:
  (2)

Iz ove dve jednakosti ( (1) i (2) ) eliminišimo h:

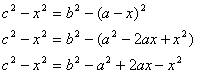
i rešimo po x:

Ovako dobijeno x uvrstimo u jednu od jednakosti (1),(2)(u (1) na primer):

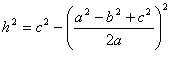
Koristeći obrazac za izračunavanje razlike kvadrata, izraz se transformiše u:

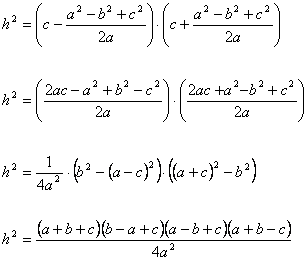
tj . 

 Znajući obrazac za izračunavanje površine trougla kojem je poznata stranica i njoj odgovarajuća visina (), dobijamo:

Aproksimacija kvadratnog korena broja koji nije potpuni kvadrat

U svojim radovima Heron Aleksandrijski se umnogome oslanjao na znanja drevnih civilizacija. Tako, za izračunavanje kvadratnog korena broja on koristi metod koji je bio poznat Vaviloncima, 2000 godina pre njegovog vremena.

˝A propo trougla stranica dužina 7,8 i 9 Heron daje metod aproksimacije iracionalnog broja.
U ovom slučaju poluobim trougla iznosi 12 ( s=12), a ostale značajne vrednosti su : s-a=5, s-b=4  i s-c=3, pa je ∆==
''Pošto 720 nema racionalan koren '', kaže Heron, ''njega možemo dobiti uz veoma malu grešku na sledeći način: Pošto je sledeći potpuni kvadrat broj 729 čiji je koren 27, podelimo 720 sa 27. Dobija se 26  . Dodajmo 27 (53) i oduzmimo polovinu od ovoga ili 26  . Koren broja 720 stoga biće veoma blizu 26 .
Zapravo,ako pomnožimo 26  sa samim sobom , proizvod je 720  tako da je razlika između ove dve vrednosti samo   .
Ali, ako želimo razliku manju od , treba da uzmemo 720  umesto 729 (ili pre da uzmemo 26  umesto 27) i uz isti postupak naći ćemo da je odstupanje od rezultata mnogo manje od   .''
Drugim rečima, ako imamo broj A koji nije potput kvadrat, a a  je najbliži potpuni kvadrat tako da je A= a±b, onda imamo
=
kao prvu parametrizaciju broja   .
Za drugu aproksimaciju uzmimo
=   
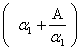
i tako dalje.
Zamenom vrednosti A sa a2±b u (1) dobijamo

 =a  
Heron, izgleda, nije koristio ovu formulu sa negativnim znakom, osim za broj   koji dat kao 7. Bez sumnje, ovo je dobijeno iz (1) na sledeći način: .
Gore navedeno predstavlja obično pravilo za nalaženje druge i daljih aproksimacija iracionalnog broja. Međutim, iako Heron ovde pokazuje kako izračunati drugu aproksimaciju(korišćenjem formule (2)), izgleda da on sam nigde ne primenjuje ovaj metod. Pitanje kako je onda dobio aproksimacije tačnije od prve (a one su nađene u njegovim spisima) i dalje ostaje otvoreno!˝

Aproksimacija kubnog korena broja koji nije potpun kub

Izračunavanje   : ˝Uzmite kubne brojeve koji su najbliži broju 100. To su 64 i 125. Izvršite sledeće operacije:
125-100=25 i
100-64=36
Zatim, pomnožite 5 sa 36 i na rezultat (180) dodajte 100. Dobićete 280. Podelite 180 sa 280. Dobijeni broj () dodajte kubnom korenu manjeg kubnog broja (4).
Ovo je najbliža aproksimacija kubnog korena broja 100.
Pokušajmo da, iz ovog primera, izvedemo Heronovu formulu za izračunavane kubnog korena.
Ako je , pretpostavimo da je A-a  . Najbolju pretpostavku da je   tražena formula dao je Wertheim.Zaista, 5∙36 može biti   , a 100+180 u imeniocu razlomka može biti polazni broj A, a ne 4∙25 ili  a∙. Međutim, Wertheimova pretpostavka je zadovoljavajuća jer može biti izvedena jednostavnim razmatranjem. Ovo je na sledeći način pokazao G.Eneström: Koristeći istu notaciju, Eneström dalje pretpostavlja da je x  tačna vrednost   i da je . Odavde sledi:
 

Slično, iz   dobijamo: 

Dakle:

rešavajući po x-a , dobijamo:
 
ili

Pošto su   kubovi razlomaka, možemo ih zanemariti u prvoj aproksimaciji i dobićemo:
  , traženu formulu za izračunavanje kubnog korena ˝
Značajan je broj Heronovih radova iz oblasti matematike i mehanike koji su do danas sačuvani. Međutim, njegovo najpoznatije delo, Metrika,otkrivena je tek krajem XIX veka. Iako je Heronu osporavano autorstvo za neka od njegovih najpoznatijih radova i mada su neki kritičari smatrali da je on prepisivao sadržaje svojih knjiga pritom ne razumevajući materiju koju izlaže,jedan od najpoznatijih među njima, Tomas Hit, je istakao:
˝Praktični značaj Heronovih dela je toliko veliki, da uopšte ne čudi to što su najpopularnija među njima bila ponovo izdavana uz ispravke i dodatke mnogo godina kasnije. Ovo je bilo neizbežno sa knjigama koje su, kao Euklidovi Elementi, bile vekovima u redovnoj upotrebi u grčkom, vizantijskom, rimskom i arapskom obrazovanju.˝

Korišćena literatura

1.˝A history of Greek Mathematics˝ , Thomas Heath (Istorija grčke matematike , Tomas Hit)
2. ˝A manual of Greek Mathematics˝ , Thomas Heath
3. ˝Science Awakening˝ , Van der Waerden
4. ˝Heron of Alexandria˝ - članak engleskih autora J.J. O’Conora i E.F. Robertsona (www.gap.dcs.st.and.ac.uk/~history/Mathematicians)

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi