Kalendari - nekad i sad

Reč kalendar potiče od latinske reči calendarium, koja označava registar kamata, odnosno računovodstvenu knjigu.Sama reč, pak, očigledno potiče od reči calendae ( ili grčki kalendae), što je naziv za prvi dan u mesecu, po starom republikanskom kalendaru.Na taj dan su proglašavani dies fasti (neradni dani namenjeni svečanostima) i dies nonfasti (pazarni,radni dani) u mesecu.
Kalendar se obično definiše kao sistem za podelu vremena u (duže) intervale poput dana,meseci i godina i rasporedjivanje tih podela u definisan red.Kalendari se pre svega sastavljaju radi uredjivanja civilnog života,jer bi bilo prilično nepraktično da danas živimo u nekom 2.567.824 danu.
Kalendari su kroz istoriju zadavali velike muke kako astronomima,tako i običnom narodu.Bilo je raznih pokušaja utvrdjivanja pravila za pravljenje kalendara.Mnogi od njih su bili toliko nepravilni da su dovodili do raskoraka sa stvarnim tokom vremena. Koliki je značaj kalendara ilustruje i činjenica da još uvek postoji i koristi se oko 40 različitih kalendara. Srešćete i najveće intelektualce današnjice koji sa beskompromisnom tvrdoglavošću i ubeđenjem koriste vrlo nefunkcionalne, ali ''njihove'' kalendare. Nijedan pokušaj konvencionalne unifikacije na osnovi dobre volje i naučno-stručnog opravdanja nije u svetu dobio veću podršku i realizaciju od nekoliko desetina procenata svetske populacije.

Astronomske osnove pravljenja kalendara

  Na početku ćemo definisati pojmove vezane za prividno dnevno kretanje nebeske sfere, prividno godišnje kretanje Sunca i prividno kretanje Meseca,da bi utvrdili pravila za računanje sa većim razmacima vremena.

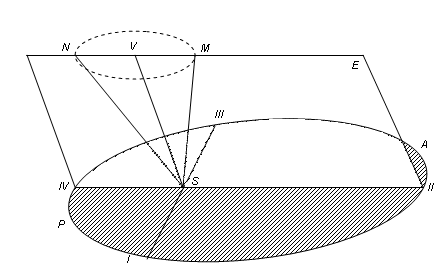
”Neka na slici tačka S predstavlja centar Sunca, PIAIIIP godišnju putanju Zemlje oko Sunca.Zamislimo li u tački S na ravan Zemljine putanje podignutu normalu SV i povučenu pravu SN,paralelnu osi Zemljine rotacije, onda nam ugao VSN predstavlja nagib Zemljine ose ili kosinu ekliptike.Ravan E položena kroz prave SV i SN stoji normalno na ravni Zemlje iseče je duž prave II IV.Tačke II i IV predstavljaju ,kao što je lako uvideti solsticijalne položaje Zemlje na njenoj putanji.Solsticijum je vreme kad Sunce dostiže svoj najviši položaj iznad ekvatora(21.jun ili 21.(22.)decembar).Prava povučena u ravni te putanje, normalno na pravu 
II IV preseca tu putanju u tačkama I i III, koje nam predočavaju ekvinocijalne položaje Zemlje.Ekvinocijum ili ravnodnevnica je vreme kada je obdanica jednaka noći.Sunčevi zraci su upravni na polutar, krug osvetljenosti prolazi kroz polove.Tačke ekvinocijuma su 20.(21.) mart,kada počinje proljeće i 21.(22.) septembar kada počinje jesen severno od polutara.”[3]
Tropska godina (Sunčeva godina) je vremenski period, koji protekne izmedju dva uzastopna prolaska Sunca kroz prividne fiksne tačke ekvinocijuma ili solsticijuma.Pojam koji takodje ima veliki značaj za pravljenje kalendara je sinodički mesec ili lunacija.
Sinodički mesec ili lunacija predstavlja kompletan ciklus mesečevih faza posmatrano sa Zemlje.

Kalendari u starim civilizacijama

 Postoje dva metoda za pravljenje kalendara: jedan se bazira na Mesečevom kretanju, a drugi koristi Sunce i njegovo prividno kretanje po nebu. Sunce nam daje godinu – kalendar sa godišnjim dobima – ali najstariji kalendari koje poznajemo su bili ipak zasnivani na kretanju Meseca. Vremenski periodi koji su određeni pomoću Meseca ne odgovaraju tačno onim dobijenim posmatranjem Sunca i to dovodi do pojave problema oko utvrđivanja i prikazivanja datuma Uskrsa u odgovarajućim terminima našeg solarnog kalendara.
  Osnovni elemenat u računanju vremena u svim kalendarima, ona jedinica čiji zbir čini jednu godinu, jeste dan. U naše vreme je uobičajeno da se danom smatra vreme proteklo između dve ponoći ali tako nije bilo i u dalekoj prošlosti. Astronomi su, na primer, od II veka pa sve do 1925. godine računali jedan dan kao vreme proteklo od podneva jednog dana pa do podneva sledećeg dana.
U starim civilizacijama kao i u mnogim primitivnim narodima, gde su međusobne komunikacije sa drugim plemenima ili kulturama bile retke, različite metode računanja dana nisu predstaljale neku teškoću jer je svako u svojoj sredini znao o čemu se radi bez obzira od kad do kad se sâm period računao. Vavilonci, Jevreji kao i stari Grci su, na primer, računali dan od jednog zalaska Sunca do sledećeg zalaska. Kroz dugu istoriju ljudske civilizacije i sama podela dana je imala puno varijanti. U drevnom Vavilonu, a kasnije u Grčkoj na primer, astronomski dan je bio drugačije izdeljen od gradskog, civilnog, koji se, kao i u drugim starim kulturama, delio na "časove". Dužina tih časova nije bila 60 minuta kao danas i nije bila konstantna, već je varirala sa promenama godišnjih doba. Podelu dana na 2 x 12 časova, odnosno 24 časa, ostavili su nam u nasleđe drevni Vavilonci, kao deo sumerskog seksagesimalnog sistema računanja, baziranog na gradaciji broja 60 (5 x 12 = 60), a ne na decimalnoj (dekadnoj) gradaciji, gradaciji broja 10, koju mi danas koristimo.
Problem svih kalendara u ljudskoj istoriji bio je u tačnom utvrđivanju broja dana u toku jedne godine. Jako davno je bilo utvrđeno da godina ne traje ceo broj dana, što je dovelo do toga da su kalendarske godine najčešće bile kraće od prirodne, astronomske godine. Tropska godina prosečno traje 365,24218967 dana ili 365 dana 5 sati 48 minuta i 46 sekundi. U računima se uzima da tropska godina traje 8765,81256 časova ili 3,1567 x 107 sekundi.
Još stari narodi su podelili godinu na mesece jer je godina, navodno, predugačka vremenska jedinica, te je zbog toga nezgodna za praćenje radnji i događaja koji traju mnogo kraće.Takvo shvatanje nameće stav da su ljudi najpre definisali godinu, a zatim je podelili na mesece. Po svoj prilici, bilo je obrnuto.Mnogo je ljudima u prošlosti bilo lakše da prate Mesečeve mene i da pomoću njih računaju vreme. Bilo je sasvim prosto ustanoviti koliko dana prođe od jednog mladog Meseca do drugog ili od jednog punog Meseca do sledećeg. Taj ciklus kretanja Meseca oko Zemlje traje približno 29 ½ dana, pa pošto nije mogućno podeliti dan tako da jedna polovina pripadne jednom mesecu, a druga drugom, drevni astronomi su računali da jedan mesec traje 29 dana, a sledeći 30, naizmenično, cele godine.
Mi u našem jeziku koristimo istu reč mesec i za Zemljin satelit i za vreme od (oko) 30 dana (engl. Moon i month). Lunacija traje 29,5305889 dana ali se računa približno 29,5 dana. Zato 12 lunarnih meseci traju 354 dana (6 x 29 + 6 x 30 = 354), što je za 11 dana manje od tropske (proste) godine, odnosno 12 dana od prestupne. Zato je uobičajeno je da se takva godina od 12 lunarnih meseci naziva lunarnom godinom, da bi se tako odmah predočio evidentirani manjak od 11 dana u odnosu na tropsku godinu.
Smatra se da su još stari Haldejci( Haldeja, nizija u donjem toku sliva Tigra i Eufrata, u kojoj je stvorena jedna od najstarijih civilizacija. Haldejsko carstvo je osnovano oko 2700 p.n.e. od strane kraljeva grada Akada) u III ili u IV milenijumu pre Hrista koristili lunarnu godinu podeljenu na 12 meseci. Od toga je šest meseci bilo sa 29, a šest sa 30 dana, što je ukupno činilo godinu od 354 dana. Primetivši da ovaj broj ne odgovara trajanju stvarne (prirodne ili kako mi danas kažemo, tropske ili sunčeve) godine, njihovi žreci su uveli svake treće godine prestupnu godinu koja je imala 13 meseci, ne bi li tako svoj kalendar doveli u sklad sa prirodom.Drevni grad Vavilon, prestonica Vavilonijeu Mesopotamiji, koji se prvi put pominje oko 4000 p.n.e., bio je dugo vremena centar napretka i nauke, posebno astronomije. Poznata je iz istorije biblijska Vavilonska kula koja je služila kao astronomska opservatorija. Vavilonci su godine određivali tako što su se oslanjali na kretanje Meseca. I njihova je godina imala 12 meseci ali su svi meseci imali po 30 dana, što je činilo ukopno 360 dana. To je bilo znatno preciznije ali je još uvek nedostajalo 5 dana do 365, te su i oni uveli prestupnu godinu sa 13 meseci. Taj mesec je imao 25 dana i dodavan je svakoj petoj godini.To narušavanje harmonije od 12 meseci sa po 30 dana dodavanjem svake pete godine tog trinaestog meseca, u narodu je smatrano kao predznak nesrećâ. Tog meseca se niko nije prihvatao nekog ozbiljnijeg posla. Ta praznoverica se održala do današnjeg dana verovanjem da je broj 13 donosi nesreću.Već tada je Vavilonski kalendar postao solarni, jer su svi njihovi meseci imali po 30 dana, a ne kao kod Haldejaca 29 i 30.
I egipatski kalendar je vremenom izgubio svoju vezu sa lunarnim, a pogotovu kasnije iz njega izvedeni julijanski kalendar. Kada ga je 45 p.n.e. Cezar ozakonio, to je bila prepravljena verzija solarnog, a ne lunarnog kalendara. Taj kalendar je sve do 8. g. p.n.e. imao 12 meseci u godini sa naizmeničnim brojem dana u mesecima od 30 odnosno 31 dan; izuzetak je bio jedino februar sa 29 dana, odnosno sa 30 u prestupnoj godini.Današnji broj dana u mesecima, kao što ćemo već videti, uveden je u vreme Oktavijana Avgusta.
Gregorijanski kalendar, koji se danas najmasovnije upotrebljava u svetu, kao i julijanski iz koga je nastao, jeste solarnog tipa. Međutim, današnji muslimanski kalendar je potpuno lunarni, dok je jevrejski kombinacija solarnog i lunarnog: podseća na vavilonski, jer u prestupnoj godini dodaju 13. mesec. To isto rade i Kinezi u svom kalendaru.U svim kalendarima, meseci kao vremenske jedinice sadrže ceo broj dana – 29, 30 ili 31. Međutim, ima i izuzetaka: indijski crkveni kalendar ima mesece čija je dužina trajanja od 29,2 do 31,2 dana.

Julijanski kalendar

 Reformator rimskog kalendara je Cezar (100 – 44 p.n.e.), najčuveniji vojskovođa slavne rimske imperije. Reforma je izvršena po sugestijama egipatskog matematičara i astronoma, čuvenog Sosigena iz Aleksandrije, a po Juliju Cezaru se i danas naziva julijanski kalendar.
Za osnovu julijanskog kalendara uzeta je sunčeva ili tropska godina, za koju smo rekli da je vremenski period koji protekne između dva uzastopna prolaska Sunca kroz prividne fiksne tačke na njegovoj putanji, a koje mogu da budu tačke ekvinocijuma ili solsticijuma. Godina je bila podeljena na 12 meseci, od kojih je šest bilo sa po 31 dan, šest sa 30, a jedan sa 29 dana. Početak godine, koji je do tada bio 1. marta, promenjen je i prebačen na 1. januar.Ovako podeljena na mesece, godina je imala 365 dana ( 31x7 + 30x4 + 28x1 = 365 ). Zbog toga je odlučeno da svaka četvrta godina ima jedan dan više (366 dana) i da bude prestupna. U prestupnoj godini mesec februar je imao 30 umesto normalnih 29 dana.Uvođenjem prestupne godine, postignuto je da svaka četvrta godina bude duža za jedan dan, što je dovelo do toga da je sada prosečna dužina godine iznosila 365,25 dana, odnosno 365 dana i ¼ dana (što iznosi 365 dana i 6 časova). Time se postiglo da je kalendarska godina bila duža od prirodne za razliku od 365,2500 – 365,2422 tj. za 0,0078 dana. Kada se to preračuna u minute, ta razlika iznosi 11 minuta i 13,92 sekunde. Obično se u računima uzima da je razlika 11 min. 14 sec.

Ipak, čak i zbog ove naoko male razlike, nekoliko stotina godina od njegovog usvajanja, ljudi bliski crkvi su zapazili da se zakonski kalendar ne poklapa sa prirodnim. Zakonski ide napred! Takođe, greška u kalendaru je dovodila i do netačnog određivanja datuma Uskrsa i ostalih praznika. Julijanska godina je bila duža od prirodne za 11 min. 14 sec., što je za proteklih 400 godina, koliko je prošlo od Cezarevog usvajanja kalendara, dovelo do toga da je kalendarska godina bila duža za čitava 3 dana. Za tih 400 godina ona je "žurila" za 4492,8 minuta, ili preračunato, 3 dana, 2 sata, 52 minuta i 48 sekundi! Za sledećih 400 godina ta razlika bi narasla i iznosila bi 6 dana, 5 sati, 45 minuta i 36 sekundi. To je značilo da na svakih 100 godina kalendarska godina biva duža od prirodne, kosmičke godine, za 18 h 43' 12''.Tako je 325. godine, kalendarska, julijanska ravnodnevica padala 24. marta, dakle 3 dana posle stvarne, 21. marta.

Gregorijanski kalendar 

               Videli smo da je srednja julijanska godina duža od prirodne (tropske) za ~11 minuta i 14 sekundi. Pošto se ta razlika stalno akumulira, ona za približno 128 godina iznosi 1 dan.Za 400 godina ta razlika naraste na 3 dana 2 sata 52 minuta i 48 sekundi, a za 800 godina naraste na 6 dana 5 sati 45 minuta i 36 sekundi. Da zvanični kalendar ne bi išao (žurio) ispred prirodnog, bilo je potrebno izvršiti njegovu prepravku.Rimski papa Gregorius (Grgur) XIII je 24. februara 1582. godine obznanio reformu do tada postojećeg, julijanskog kalendara, predloženu od strane nemačkog jezuite i astronoma Christophera Claviusa,a uz pomoć napuljskog astronoma i fizičara Aloysiusa Liliusa. Papina bula (ili dekret) koji je sadržavao tu reformu nazvana je Inter Gravissimas, po prve dve reči u tom tekstu. Te reči na latinskom jeziku znače "među najvažnijim …"

Donešene su sledeće odredbe:

1.   Kada je papa 1582. godine promenio kalendar, prolećna ravnodnevica (21. mart) je padala čitavih 10 dana posle ovog astronomskog događaja. Zato je odlučeno da se briše (izostavi) 10 dana iz kalendara, tako što iza četvrtka 4. oktobra 1582. godine odmah dolazi petak 15. oktobra 1582. godine (umesto 5. oktobra!)
2.   Pravilo ustanovljeno i primenjivano u julijanskom kalendaru da je svaka četvrta godina prestupna, menja se. U novom, gregorijanskom kalendaru prestupna je svaka četvrta, kao i sekularne godine (godine stoleća, one koje se završavaju sa 00) koje su deljive sa 400.
3.   Dan viška prestupne godine stavljaće se iza 28. februara.
4.   Novo pravilo za određivanje datuma Uskrsa. (Staro pravilo bilo je bazirano na julijanskom kalendaru.)
5.   Prvi dan u godini (Nova godina) biće 1. januar.
  U gregorijanskom kalendaru tropska godina iznosi približno 365 97/400 dana = 365,2425 dana, a prema današnjim proračunima stvarna prosečna dužina solarne godine iznosi 365,2421890 dana.Aproksimacija 365 i 97/400 se odnosi na 97 prestupnih na svakih 400 godina.Razlika iznosi 0,2425 – 0,2421890 = 0,00031 dan ili kada bi preračunali u sekunde, ta bi razlika iznosila: 0,00031 x 86.400 = ~26 sekundi.Za toliko je prosečna gregorijanska duža od prosečne tropske godine? Prostim računom se dobija da će ta razlika da se akumulira do vrednosti od 1 dan tek za 86.400 : 26 = ~3.320 godina, odnosno da bi se tropska godina pomerila za 1 dan u odnosu na dati kalendar.Međutim, znamo da će oko 5000–te godine solarna godina trajati 365,24201 dan, pa će razlika između kalendara i tropske godine biti povećana na 0,00059 dana. To nam jasno govori da vremenom gregorijanski kalendar postaje sve netačniji.
Već smo rekli da gregorijanski kalendar ima 97 prestupnih godina na svakih 400, a ne 100 kao julijanskiSvaka godina koja je deljiva sa 4 jeste prestupna.Međutim, svaka godina deljiva sa 100 (sekularna ili vekovna godina) nije prestupna godina.Dakle, svaka godina deljiva sa 400 je prestupna godina.Tako imamo da sekularne godine 1700., 1800., 1900., 2100., 2200., itd nisu prestupne ali zato jesu 1600., 2000., 2400., itd.

Ciklus zlatnog broja- Metonov lunarni ciklus

 Svaka kalendarska godina je u odgovarajućoj vezi sa zlatnim brojem. Obzirom da se odnos između mesečevih mena (faza) i dana u kalendaru tokom jedne godine ponavlja u ciklusu od 19 godina, odnosno potrebno je 19 godina da jedna mesečeva mena padne ponovo u isti dan, prirodno je napraviti vezu brojeva koji se nalaze između 1 i 19 (uključijući i njih) i kalendarske godine. Taj odnos je nazvan zlatni broj i izračunava se ovako: 
Zlatni broj = (broj godine mod 19) + 1
Najznačajniji od svih ranih pokušaja da se obezbedi nekakva proporcionalnost između religijskog lunarnog kalendara i tropske godine bio je tzv. Metonov ciklus. Njega je 432 p.n.e. otkrio i formulisao grčki astronom po imenu Meton iz Atine. On je (radeći zajedno sa drugim atinskim astronomom Euctemonom) izveo čitav niz posmatranja vezanih za solsticijum, mereći kada je dužinu podnevne senke štapa – kazaljke gnomona (Sunčani časovnik sa vertikalnim štapom; od oko 3500 p.n.e.) najveća odnosno najmanja, da bi time odredili dužinu trajanja tropske godine. Uzimajući da sinodički mesec tj. jedna lunacija ili lunarni mesec traje prosečno 29 ½ dana, izračunali su tada da razlika između 12 takvih lunacija i njihove tropske godine koju su izmerili iznosi 11 dana.To neslaganje je moglo biti neutralisano ubacivanjem (interkalacijom) još jednog meseca u kalendaru svake treće godine koji bi imao 33 dana. Ipak, želeći da iznađu jedno dugoročno pravilo o usklađivanju lunarne i tropske godine, Meton i Euktemon su računom došli do 19–ogodišnjeg ciklusa. Meton je kalendar podelio u periode od po 19 godina, a svaku godinu označio brojem od 1 do 19 i zaključio da će mlad Mesec uvek pasti u isti dan u godinama koje su označene istim brojem (Zlatni broj).Ciklus sadrži 12 godina, od kojih svaka ima po 12 lunarnih meseci i 7 godina od kojih svaka traje 13 lunacija – ukupno 235 lunacija. (12 x 12 + 7 x 13 = 144 + 91 = 235). Trinaesta lunacija je bila poznata kao ubačeni (embolični) mesec.Ako uzmemo da ovih 235 lunacija sačinjava 110 "krnjih" meseci od 29 dana i 125 "punih" meseci sa po 30 dana, dobićemo ukupno (110 x 29) + (125 x 30) ili 6940 dana.Za period od 19 godina, razlika između lunarnog kalendara (6940dana) i solarnog, od 365dana (19 x 365 = 6935 dana) iznosila je svega 5 dana, što je mnogo manje od do tada izmerenih 11 dana razlike svake godine, tako da je prosečna vrednost za tropsku godinu bila ne više 365 dana, već 365,263 dana. Time se dobila mnogo tačnija vrednost tropske godine nego što je bilo po kalendaru do tada.
Ovo rešenje je oduševilo stare Atinjane, pa će jedan broj, kojim je označena tekuća godina u Metonovom ciklusu, ubuduće biti napusan zlatnim slovima na crkvenim stubovima. Da li zbog toga ili zbog važnosti otkrića, tek taj broj je nazvan Zlatni broj godine.Značaj Metonovog ciklusa je bio u tome što se kao konačno pravilo prihvatilo rešenje da se svake treće godine u lunarni kalendar ubacuje interkalarni mesec, da bi se time održao korak sa ciklusom solarnog kalendara. Tako precizno izračunata dužina tropske godine, korišćena je u jevrejskom kalendaru i u kalendaru hrišćanske crkve; uticala je i na indijska astronomska učenja.Savremeni proračuni su pokazali da 235 lunacija (sinodičkih meseci) imaju 6939 dana i 16,5 časova, a da ciklus od 19 solarnih godina ima 6939 dana i 14,5 časova. Razlika je svega 2 sata.
Metonov ciklus je poboljšao grčki astronom Callipus (Callippus iz Cyzicusa, danas grad na Mramornom moru u Turskoj, (oko 370–300 p.n.e.), verovatno najistaknutiji astronom svog vremena. Dodao geocentričnom sistemu Merkurovu i Venerinu sferu).On je formirao tzv. Kalipusov period, koji je predstavljao četvorostruki Metonov ciklus. On sadrži 4 x 19 = 76 godina, odnosno 4 x 235 = 940 lunarnih meseci. Umesto da ima ukupno 440 meseci od 29 dana i 500 meseci sa 30 dana, Kalipusov period sadrži 441 nepunih meseci i 499 punih meseci, čime je smanjio dužinu četiri Metonova ciklusa za 1 dan.Na taj način se dobija ukupno:
(441 x 29) + (499 x 30) = 27.759 dana.
Ako se ovaj broj podeli sa (19 x 4) = 76, dobija se tačno 365,25 dana.
Hipparchos (Hipparchus sa Rodosa, grčki astronom i matematičar rođen 146., a umro posle 127 p.n.e.), je bio možda najveći posmatrač među astronomima antike. Posmatrajući zvezdu Spiku u sazvežđu Device on je, preko 150 godina pre ostalih, prvi utvrdio da tačka ravnodnevice, tj. mesto gde ekliptika (sunčeva vidljiva putanja) preseca nebeski ekvator (nebeski ekvivalent Zemljinom ekvatoru), nije neka fiksna tačka u prostoru, već da se lagano pomera u pravcu zapada. To pomeranje je veoma sporo, ne više od 2°na 150 godina i naziva se precesija ravnodnevice.Kalendarski, ovo je bilo veoma važno otkriće, jer se tropska (sunčana) godina određuje prema ravnodnevici, a precesija smanjuje vrednost koju je izračunao Kalupus. Hiparh je time dobio vrednost tropske godine od 365,242 dana, što je neverovatno blizu današnjem proračunu od 365,24218967 dana.Takođe je izračunao i preciznu dužinu lunacije koristeći veliku godinu, četiri Kalipusova perioda. Došao je do vrednosti od 29,53058 dana, što je ponovo jako blizu danačnjoj vrednosti od 29,53059 dana.

Milutin Milanković-reforma julijanskog kalendara

 Milutin Milanković (1879 - 1958) je po profesiji bio građevinac, astronom, matematičar, geofizičar, ali iznad svega utemeljivač moderne klimatologije i klimatskog modeliranja.Radio je i kao profesor na Beogradskom univerzitetu.Milankovićev značaj za nauku je u rangu sa dostignućima naših velikih naučnika, poput Tesle, Pupina, Cvijića, Mike Alasa ili Pančića, ali i drugih naučnika iz čitavog sveta.
 Milankovićev kalendar je do sada najpreciznije urađen kalendar. Gregorijanski je sadržavao dva krupna nedostatka: za godinu je uzimano da ima 365 i 1/4 dana i da 235 lunarnih meseci predstavlja tačno 19 solarnih godina. Milanković je svoj kalendar bazirao na anulaciji tadašnjih 13 dana, novi kalendar je doveden na isti datum kao Gregorijanski, prestupne godine mogu biti one koje su deljive sa 4 bez ostatka, a sekularne godine biće samo onda prestupne ako njihov broj vekova kada se podeli sa 9 daje ostatak 2 ili 6. Sve ostale sekularne godine su proste, što daje potpunu preciznost do 2 800. godine, odnosno do tada ne može biti nikakvog razmimoilaženja sa sadašnjim Gregorijanskim kalendarom. Razlika između Milankovićeve i tropske godine iznosi svega 2 sekunde godišnje Ovako koncipiran Milankovićev kalendar je trebalo korigovati tek posle 28 800 godina, ali, nažalost, ni do dana današnjeg, iako je u suštini prihvaćen na Svepravoslavnom kongresu 30. maja 1923. godine u Carigradu, nikada nije zaživeo.

 A sada da se udaljimo za trenutak od astronomske stvarnosti i odemo u područje pretpostavki tipa "šta bi bilo kad bi bilo …".Kada bi Mesečeva orbita bila samo malo duža, pa da njegovo obilaženje oko Zemlje sa zapada na istok traje 30 umesto 29,53059 dana, što bi za 11 časova 15 minuta i 57 sekundi produžilo sadašnje vreme obilaska Meseca oko Zemlje, onda bi 12 lunarnih meseci činilo godinu od 360 dana.Da bi sunčana godina trajala 360 dana, bilo bi potrebno da se Zemljina orbita smanji i da njen obilazak oko Sunca bude kraći za 5,2422 dana.Tada bi svi meseci imali po 30 dana i ne bi bilo potrebe za prestupnim godinama. Tada bi nestale razlike između solarnog i lunarnog kalendara. Postojao bi samo jedan jedinstveni kalendar za ceo svet; hrišćanski, muslimanski, jevrejski, kineski … bili bi isti.

Literatura

[1] Dr Branislav Ševarlić, Dr Zaharije Brkić, Opšta astronomija, Naučna knjiga,Beograd,1981 

[2] Milan Božić,Pregled istorije i filozofije matematike,Zavod za udžbenike i nastavna sredstva,Beograd 2002

[3] Milutin Milanković,Istorija astronomske nauke,Naučna knjiga,Beograd,1979

[4] Milutin Milanković,Kroz vasionu i vekove,Dereta,Beograd,2002

[5] Prof. dr Stevo Šegan,Kalendari-pregledni članak,Katedra za astronomiju Matamatičkog fakulteta,april 2003

[6] www.astronomija.co.yu/knjige/kalendar,Drago Dragović,Kalendari kroz istoriju 

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi