ИНВЕРЗИЈА У ОДНОСУ НА КРУГ 

 1. Историја еуклидске геометрије

 Геометрија је као наука поникла из свакодневне праксе.Људи су морали градити домове и зграде,одређивати границе земљишта и њихове димензије. Нема- лу улогу с тим у вези имале су и уметничке потребе људи као што је жеља да украсе своје домове и одећу и да стварају слике из живота који их окружује. Све је то захтевало од људи да упознају просторна својства објеката материјалног све- та и да проучавају законитости на које при томе наилазе.Те су законитости не биле провераване и потврђиване многобројним опажањима и експериментима, а добијена сазнања су се преносила са генерације на генерацију, у почетку усмено, а затим и писмено.
Неколико векова пре наше ере,културни народи су располагали подацима
о просторним особинама предмета,знали су мерити дужине,површине и обиме,и  та своја знања примењивали су у пракси.Потребно је истакнути да та знања нису систематизирана,већ формулисана у облику правила и рецепата. На формирање геометрије као науке значајан утицај су имали старогрчки филозофи и мислиоци.
Међу њима најистакнутији из тог времена био је Аристотел, који је живео од 384. до 322. године пре наше ере.
Постављање аксиома геометрије и испитивање њихових узајамних односа,био је задатак грчких мислилаца још од 5.века старе ере.Највећи утицај на каснији развитак геометрије имао је геометријски састав изложен у раду  Елементи математичара Еуклида.

 Еуклид  (330.-275.год. пре нове ере), је познати грчки математичар.Живео је и радио у Александрији где је створио математичку школу.Радови Еуклида су сакупљени у тринаест књига под заједничким насловом Елементи,који су написани око 300.године старе ере.У свом делу Елементи Еуклид је сакупио и логички прерадио достигнућа претходних епоха у области геометрије.Такође је ту први систематично засновао теорију бројева,доказао бесконачност низа простих бројева и засновао теорију дељивости.
Елементи су далеко најчувеније и најчитаније дело из тог времена.Утим је књигама обухваћена углавном сва геометрија која се данас учи у средњој школи.
Еуклидови Елементи су током 2000 година представљали основно дело из којег се учила геометрија.Оно је било преведено на језике свих  културних народа света.Захваљујући делу какво је Еуклидови Елементи,геометрија је вековима доживљавана као савршенство,а сва остала систематизована знања равнала су се према њој и са њом упоређивала. Даљи развитак геометрије одвијао се у смеру усавршавања Еуклидових Елемената,исправљању уочених нетачности и додаванју нових теорема.Посебну пажљу геометричара је привукао је ПЕТИ ЕУКЛИДОВ ПОСТУЛАТ.

Развој геометрије од античких времена је ишао у два правца.Систем аксиома је прошириван тако да би се могао доказати што већи број тврђења,док се је са друге стране упорно покушавало доказивање петог Еуклидовог постулата.
Усавршавањем Еуклидових дела бавили су се:Архимед(од 287.до 212.год.старе ере),Аполоније(3.век пре нове ере),Геминиус,Никомах(1.век пре нове ере),Папос(3.век нове ере),Теон и Прокло(5.век нове ере).

 Аполоније (262.-190.год.пре нове ере) је антички хеленски математичар и астроном,познати научник александријског Музеона.Рођен је у Пергаму,граду у јужном делу Мале Азије.Аполоније почиње школовање у Ефесу код Еудема Пергамског,а Еудем га саветује да школовање настави у Александрији.У Александрији учи од Еуклидових ученика.Први радови које објављује су из астрономије, а потом углавном пише математичка дела.Најпознатија дела су Купини пресеци у 8 књига.Аполоније у првој књизи својих Купиних пресека помиње Еуклидове Основе купиних пресека.Ово дело му доноси звање ВЕЛИКИ ГЕОМЕТАР и велико поштовање међу ученим људима.
Aрапски историчар Ibn an Nadimпише да су сем Конусних пресека  била позната и следећа дела: 1.Односи пресека,(латински:De Rationis Sectione),у две књиге са 180 теорема, 2.О одређеним односима,у две књиге, 3.О подели ликова у сразмери,у једној књизи и 4.О додирујућим круговима.

 Током низа векова,без обзира на напоре који су чињени,нико није успео да суштински унапреди геометрију као науку у односу на оно што је било изнето у Еуклидовим Елементима.
Тек у деветнаестом веку решен је проблем да се изведе доказ петог посту-
лата.Кроз рад Николаја Ивановича Лобачевског(1792-1856.) и Јаноша Бољаја(1802-1860.) први пут је изражена мисао и доказано је да пети Еуклидов постулат не зависи од осталих аксиома геометрије и да се самим тим не може извести његов доказ.
Пети Еуклидов постулат:Ако две праве а и b у пресеку са трећом правом с граде супротне углове чији је збир различит од збира два права угла,онда се праве а иb секу и то са оне стране сечице са које је тај збир мањи од збира два права угла.

С једне стране је његова формулација врло сложена у поређењу са другим постулатима и аксиомама,а с` друге стране сама се тврдња постојања сечице није чинила толико очитом и изван сваке сумње,као тврдње изречене у осталим аксиомама и постулатима.Узрок томе је чинењица што се у петом постулату први пут појављује појам бесконачнога.У исто време се у осталим постулатима  описују она својства фигура која се могу лако проверити,док је таква провера петог постулата физички немогућа.Покушаји његовог доказивања довели су до низа еквивалентних тврђења.Једно од таквих тврђења је:

Плејферова аксиома паралелности: Ако је р произвољна права и А тачка ван ње тада у равни π(р,А) постоји јединствена права а која садржи тачку А и нема заједничких тачака са правом р.

 Аксиома паралелности била је позната као став још у античким  временима код Грка.Међутим Еуклидова оригинална формулација унеколико се разликује од Плејферове аксиоме паралелности,која у ствари представља еквивалент петог Еуклидовог постулата. Пошто овако исказан поседује једноставну формулацију  Плејфер 1797.године узима тај став за аксиому,а пети постулат за теорему.

 
  Сл.3. Давид Хилберт 

У свом делу Основи геометрије из 1899.године,немачки математичар Давид Хилберт(1862-1943.) засновао је геометрију на непротиворечном,потпуном и независном систему аксиома.Хилберт у свом делу уводи двадесет аксиома које разврстава у пет група.У Хилбертовом систему основни појмови су „тачка“,“права“,“раван“,“површина“ и тд.Ми наводимо нешто модификован Хилбертов систем аксиома на следећи начин:

I. Аксиоме инциденције (девет аксиома),

II. Aксиоме поретка(шест аксиома),

III. Аксиоме подударности(седам аксиома),

IV. Аксиоме непрекидности(једна аксиома),

V. Аксиоме паралелности(једна аксиома).

Аксиоматика прве четири групе сачињава аксиоматику апсолутне геометрије.

Дефиниција 1.1 Теорију засновану на систему аксиома апсолутне геометрије и Плејферовој аксиоми паралелности називамо Еуклидском или параболичком геометријом.Раван и простор у коме важе аксиоме Еуклидске геометрије називамо респективно Еуклидском равни и Еуклидским простором и означавамо са
Е² и Е³.

 ЕУКЛИДСКА ГЕОМЕТРИЈА се добро слаже са геометријом чврстих тела,па је у извесном смислу оправдано мишљење које је владало око 2.миленијума да је геометрија опажајног простора ниједна друга до еуклидска.Простор величине молекула,како је емпиријски утврђено,заиста се понаша као еуклидски.Такође и простор у коме постоје кристали је еуклидски.Међутим,геометрија простора унутар атома,како је познато,није еуклидска или,боље речено,нееуклидска геометрија једноставније описује својства субатомног простора.Слично,за истраживање просторних односа тела у космичком простору погодније је користити геометрију са променљивом закривљеношћу,која није еуклидска.

2. Трансформације еуклидске равни

 ИЗОМЕТРИЈСКЕ ТРАНСФОРМАЦИЈЕ ПРОСТОРА  Eⁿ

Дефиниција 2.1 Бијективно пресликавање I:Еⁿ→Еⁿ називамо изометријском трансформацијом простора Еⁿ, (n = 1,2,3) ако за произвољне две тачке А и В простора Еⁿ важи (А,В)   (I(A),I(B)).

Teoрема 2.1. Идентично пресликавање  (коиннциденција, јединично) ε: Еⁿ→Еⁿ,
 (n = 1,2,3) је изометријска трансформација.

Теорема 2.2. Производ било које две изометријске  трансформације простора Еⁿ је изометријска трансформација простора  Еⁿ.

Дефиниција 2.2. Осном рефлексијом равни Е² у односу на праву р називамо изометријску трансформацију Sp која није коинциденција и у којој је свака  тачка праве р инваријанта.Права р је оса рефлексије Sp.

Напомена: Из дефиниције следи да поред праве  р  у равни Е² осна симетрија нема инваријантних тачака.Реч рефлексија је коришћена уместо речи симетрија у појму осна рефлексија јер појам симетрије у геометријској теорији изометријских трансформација има шире значење  и означава сваку изометријску трансформацију која лик Φ датог простора  преводи у лик Φ´,а простор у самог себе.

Теорема 2.3. Свака изометријска трансформација равни Е² може се представити у облику композиције три осне рефлексије.

 ТРАНСФОРМАЦИЈЕ СЛИЧНОСТИ ПРОСТОРА Еⁿ

 Сада ћемо се упознати са трансформацијама сличности које представљају уопштење изометријских трансформација.

Дефиниција 2.3. Нека је k произвољан  позитиван реалан број и Ρ :Еⁿ→Еⁿ
 (n = 1,2,3) бијективно пресликавање које сваке две тачке X и Y  простора Еⁿ преводи редом у тачке X´и Y´простора Еⁿ такве да јеX´Y´= k·XY.Тада пресликавање Ρ називамо трансформацијом сличности простора Еⁿ ,са коефицијентом  k.

Непосредно из дефиниције можемо закључити да изометријске трансформације  представљају само специјалан случај трансформација сличности за k = 1.Неке од особина трансформација сличности простора Еⁿ су:

 
Теорема 2.4. Трансформација сличности Ρ  простора Еⁿ колинеарне тачке A,B,C преводи у колинеарне тачке A´B´ C´.Штавише,трансформација сличности простора Еⁿ је уређена,тј. Ако јеB ( А,В,С)тада  је B ( А,В,С).

Теорема 2.5. Трансформација сличности Ρ  подударне парове тачака пресликава
на подударне парове тачака.

Дефиниција 2.4. Трансформацију сличности Ρ  простора Еⁿ називамо ДИРЕКТНОМ или ИНДИРЕКТНОМ у забисности од тога да ли она чува или мења оријентацију тог простора.

 Композиција двеју директних или индиректних трансформација сличности
простора Еⁿ представља директнуизометријску трансформацију сличности.Такође композиција трансформација сличности простора Еⁿ од којих је једна директна а друга индиректна представља индиректну трансформацију  сличности.

Дефиниција 2.5. Нека је О произвољна тачка простора Еⁿ и к реалан број различит од нуле. Хомотетијом са средиштем  О и коефицијентом к називамо трансформацијуНо,k :Eⁿ→Eⁿ ,( n = 1,2,3) која сваку тачкуX єEⁿпреводи у тачку X´Eⁿ  такву да је´= k· .

Teoрема 2.6. Хомотетија Но, kпростора Еⁿ представља трансформацију сличности са коефицијентом k´= ׀k׀

 Teoрема 2.7. Трансформацију сличности Ρ: Eⁿ→Eⁿ која преводи сваку паралелну праву у њој паралелну праву представља транслацију или хомотетију.

ПОТЕНЦИЈА ТАЧКЕ У ОДНОСУ КРУГ

Трансформације сличности простора Еⁿ омогућују у геометрији ликова тог простора разоткривање разних метричких својстава тих ликова.Од  посебног значаја су интереса својства везана за круг.Уз помоћ потенције тачке 
у односу на круг изводе се неке од тих особина.Пре увођења дефиниције  потенције тачке у односу на круг доказаћемо теорему.

Теорема 2.8. Ако су у равни задати  круг k и тачка Р,тада  за свакy  праву sкоја сече kруг  у тачкама X Y и пролази крозтачку Р важи ·= const.Ako
je тачка Р ван круга k и Т додирна тачка  једне од тангената из тачке Р
ван круга ,тада је ·= ².


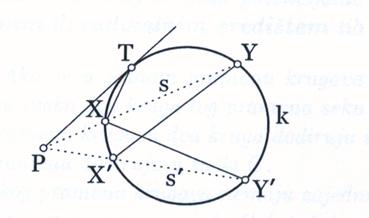
Слика 4.

Доказ: Из сличности троуглова РХТ и РYТ следи да је :

РТ : РΥ = РХ : РТ тј. РХ · РΥ = РТ ² 

Дефиниција 2.6. Константан производ·уведен претходном теоремом називамо потенција тачке Р у односу на круг k ,и означавамо саp(P,k).

 Oзначимо са ОР = d, а са А и В пресечне тачке праве РО и круга k.Тада је
Р(Р,к) = d² - r².

Teoрема 2.9. Скуп свих тачака равни Е² којима су потенције у односу на два ексцентрична круга k1(O1,r1)иk2(O2, r2) међусобно једнаке представља једну праву управну на правој О1О2.

Дефиниција 2.7.Скуп свих тачака равни чије су потенције једнаке у односу на два ексцентрична круга k1и  k2називамо  потенцијалном или радикалном осом тих кругова.

Дефиниција 2.8.Скуп свих кругова неке равни од којих свака два имају за потенцијалну осу исту праву р,назива се прамен кругова или систем коаксијалних кругова, а права р потенцијална оса тог прамена.

Teoрема 2.10. Потенцијалне осе трију кругова припадају истом прамену правих.
Скуп средишта свих кругова једног прамена припада једној правој која је ортогонална на оси тог прамена.

Дефиниција 2.9. Тачку О у којој се секу потенцијалне осе трију кругова називамо потенцијалним или радикалним  средиштем тих кругова.

Teoрема 2.11. (i) Ако се уједном прамену кругова два круга секу у тачкама А и В,онда се свака два круга тог прамена секу у тачкама А и В;
(ii)Ако се у неком прамену кругова два круга додирују у тачки С ,онда се свака два круга тог прамена додирују у тачки С;
(iii)Ако два круга неког прамена кругова немају заједничких тачака, онда никоја два круга тог прамена немају заједничких тачака.

Дефиниција 2.10. Прамен кругова у равни Е² је елиптички ако се кругови тог прамена секу у двема различитим тачкама,параболички ако се додирују и хиперболички ако немају заједничких тачака.

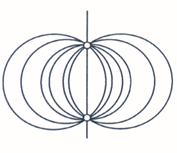
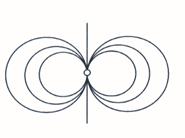
 Слика 5. Елиптички,параболички и хиперболички прамен кругова

Teoрема 2.12. За свака два круга постоји тачно један прамен кругова коме они припадају.

Teoрема 2.13. Скуп кругова ортогоналних на све кругове датог прамена представља опет прамен кругова.У том случају потенцијална оса првог прамена садржи средишта кругова другог прамена.

Дефиниција 2.11.Праменови кругова из претходне теореме називају се ортогоналним.

 3. ИНВЕРЗИЈА У ОДНОСУ НА КРУГ

 Једини нелинеарни епицикли еуклидске равни су кругови.Тиме је истакнут значај овог геометријског лика коме се у еуклидској геометрији посвећује посебна пажња.
Потенција тачке у односу на круг омогућује да у геометрији равни Е²установимо  специфичну трансформацију коју називамо инверзијом у односу на круг који се налази у тој равни.

 ОПШТИ ПОЈМОВИ

 Дефиниција 3.1.  Некаjеk(О,r)  произвољан круг равниЕ² и² =Е² \ {О}.
Инверзијом у односу на круг k   називамо трансформацију ψк : ² →² која сваку тачку Р´  ² такву да је ·´ =r²,при чему су О,Р´и Р три различите колинеарне тачке и Р и Р´су са исте стране тачке О.

Taчку О називамо центром или средиштем инверзије, дуж r –полупречником инверзије,величину r² – степеним коефицијентом, круг kкругом инверзије ψк а ²- Гаусовом равни.(слика 6.)

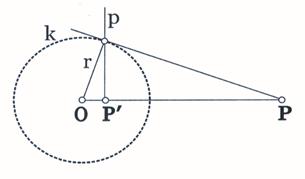
 Слика 6.

 Дефиниција 3.1. Нека је дат круг са центром О. Нека је тачка Р´ слика тачке Р различите од О при инверзији у односу на круг k. Права нормална на ОР у тачки Р´ назива се полара  тачке Р у односу на круг k, и обратно, тачка Р се назива пол  праве р у односу на круг k.

Својства:

 а ) Нека су праве р и q поларе тачака Р и  Q у односу на круг k.Тачка Р припада правој  q  акко тачка Q припада правој  р.Тачке   Р и Q називамо коњугованим у односу на  круг k  ако једна лежи на полари друге.

 b ) Пол неке тачке коњугован је у односу на све тачке те праве.

 с ) Поларе свих тачака једне праве у односу на неки круг секу се у једној  тачки ( у полу те праве у односу на исти круг).

ОСОБИНЕ ИНВЕРЗИЈЕ

 Из дефиниције инверзије непосредно следи наредно тврђење:

Теорема 3.1.  Инверзија у односу на круг је бијекција.

Доказ: Нека су X и Y  произвољне тачке  равни ² и ψк ( X) = X´, ψк (Y) =Y´.
Одавде је   ·' = · ' (=r²),па за X' Y' важи OX=OY (због OX'=OY' и   ·' = · ' (=r²)).Но како тачке X' иY'припадају полуправама OX и OY то тачке X иY при падају полуправама OX' и OY' а како је X' Y'биће иOX' OY' па самим тим и OX OYте збогOX=OY важи XY,  што значи да је инверзија
„1-1“пресликавање.
Како је   = r²/',то ће за произвољну тачку X' равни²,постојати тачка X полуправе ОX' (самим тим ће тачка X' припадати полуправој ОX) која испуњава претходну једнакост.Дакле, X' = ψк ( X),па је инверзија „на“ пресликавање.Одавде следи да је инверзија бијекција. 
Међутим,као што се може приметити инверзија у односу на круг није бијективна  трансформација целе равни Е² већ само њеног дела ²,јер у њој није дефинисана слика тачке О,нити је тачка О слика неке тачке равни Е².
Инверзију у односу на круг могуће је разматрати и у такозваној комфорној равни ,тј. Еуклидској равни Е² проширеној бесконачно далеком тачком .Тада  је
ψк ()= 0 и ψк (0) =.

 Теорема 3.2. Инверзија у односу на круг је инволуција.

Доказ: Нека је ψк : ² →²  инверзија у односу на круг k(О,r).Ако је X² произвољна тачка,тада тачка  X´= ψк ( X) припада полуправој OXпри чему је
  ·' = r² (слика 7.). Тада и тачка X припада полуправој ОX'  и важи 
  ·' = r²,па је ψк ( X' ) = X.Дакле,заиста је ψк² = ε. 


Слика 7.

Теорема 3.3. У инверзији ψк : ² →²  тачка X је инваријантна ако и само ако X припада кругу k .

Доказ: Ако је X² инваријанта имамо да је   ·  = r² па је ОX = r ,тј. тачка X припада кругу k.
Обратно,ако X  k, тада тачка X´= ψк ( X) припада полуправој ОX  и важи   ·' = r².Одавде је ОX' = r,тј. тачке X и X' се поклапају. 

Геометријско место тачака,које се поклапају са својим инверзивним у једној  равни,за исти центар О биће круг инверзије.

Теорема 3.4. У инверзији ψк : ² →²  тачки X која се налази у кругу k одговара тачка X' која се налази изван круга и обратно тачки X која се налази изван круга k одговара тачки  X' која се налази у кругу k.

Доказ: Нека је О средиште и r полупречник инверзије  ψк .Ако је X у кругу k тада је ОX < r па из релације   ·' = r² следи да је ОX' > r,тј. тачка X  је  изван круга  k.
Обратно,ако је X  изван круга  k тада је ОX > r,одакле на исти начин као малопре следи да је ОX' < r,односно тачка X' је унутар круга k. 

4. АПОЛОНИЈЕВИ ПРОБЛЕМИ О ДОДИРУ КРУГОВА

 Применом инверзије у односу на круг .могу се елегантно  решити Аполонијеви проблеми о додиру круга.Проблеми могу бити следећег  облика:

 Конструисати круг који задовољава три услова од којих сваки  има један од облика:
 
 ● садржи дату тачку,

 ● додирује дату праву,

 ● додирује дати круг.
 
 Подразумева се да све тачке, праве и кругови из поменутих  услова припадају истој равни. Неки од тих проблема се могу веома лако  решити, док за неке то није случај.

 Аполонијевих проблема има десет:

1. Конструисати круг који садржи три дате тачке.

2. Конструисати круг који садржи две дате тачке  и додирује дату праву  

3. Конструисати круг који садржи две дате тачке и додирује дати круг.

4. Конструисати круг који садржи дату тачку и додирује две дате праве.

5. Конструисати круг који садржи дату тачку и додирује дати круг и дату праву .

6. Конструисати круг који садржи дату тачку и додирује два дата круга.

7.Конструисати круг који додирује три дате праве.

8. Конструисати круг који додирује две дате праве и дати круг.

9. Конструисати круг који додирује дату праву и два дата круга.

10. Конструисати круг који додирује три дата круга.

 Oзначићемо дате параметре на следећи начин: тачке А , В , С; праве р1 , р2, р3; кругове O1 O2,O3.Тада Аполонијеве проблеме шематски можемо приказати на следећи  начин:

 Први и седми проблем су тривијални. Такође и сви остали Аполонијеви  проблеми се могу решити без примене инверзије. Међутим, инверзија даје  један општи метод за њихово решавање. Он се заснива на чинењици да се  у одређеном случају, као што смо видели, круг пресликава у праву и обрнуто.

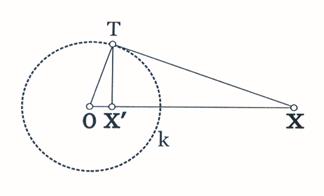
 2. Конструисати круг који садржи две дате тачке и додирује дату праву р1 .

 Анализа:Нека круг  k садржи две тачке А  и В,и додирује дату праву р1 у тачки D . При инверзији у односу на круг l(А,АВ) правој р1  , одговара круг р1'  (сл.8.) који пролази кроз тачку А  а круг k  одговара правој k'.
Како тачка В припада кругу инверзије l то ће се она пресликати у саму
себе. Права р1 са кругом k има једну заједничку тачку  те ће се исто важити и за њихове слике при инверзији, тј. права k' ће додиривати круг . Круг k садржи тачку В  која се при овој инверзији пресликава у саму себе, одакле следи  да и његова слика,права k',садржи тачку В. Према томе, ми најпре треба да констр-
 
Слика 8.

уишемо круг р1'   који је инверзна слика праве р1, у односу на круг  l(А,АВ), затим праву k' кроз тачку  В која је тангента на круг р1'  , а зтим круг k као инверзну слику  праве k'  у односу на круг l.

 Конструкција: Нека су дате две тачке А   и В  права р1 , тако да су тачке А  и В са исте стране праве р1. Конструишемо затим круг l(А,АВ) и инверзну слику праве р1  у односу на круг l. То ће бити круг р1'  ,који пролази кроз центар  инверзије А. Из тачке В конструишемо тангенту k' на круг р1'. Конструишимо  затим инверзну слику праве k'  у односу на круг l(А,АВ).То  ће бити тражени круг k.Докажимо то.

Доказ: Круг  k као инверзна слика праве  k'  пролази кроз центар инверзије А.Такође круг k  садржи и тачку В као инваријантну тачку посматране инверзије,па  је задовољен и други услов. Круг  k додирује праву р1  јер и њихове инверзне слике k' и  р1' имају  једну заједничку тачку.

 Дискусија: Под условом да су тачке А и В са  исте стране праве р1задатак има два решења јер се из  тачке В могу конструисати две тангенте на круг р1'. Случај када су А и В са разних страна праве р1 нема смисла разматрати,јер у том случају круг k у  пресеку са правом р1има две заједничке тачке. 

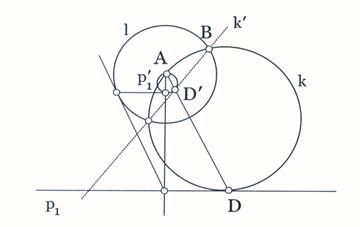
 3.Конструисати круг који садржи две дате тачке А и В и додирује  дати круг O1  .

 Нека круг k пролази кроз тачке А  и В  и  додирује дати круг O.Конструишимокруг  l(А,АВ) (сл. 9.). У инверзији у односу на дати круг l,

Слика 9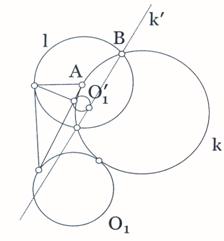

l(А,АВ) ,круг  k ће се сликати у неку праву k'  која пролази кроз тачку В, а круг O1у неки кругO1'при  чему ће права k' бити тангента круга O1' , јер се кругови k и O1'додирују. Према  томе, можемо најпре конструисати круг O1' ,који  је инверзан са кругом O1у односу на круг l(А,АВ), па  онда тангенту k' из тачке В на круг O1',и на крају инверзну слику праве k' у односу на l(А,АВ),
која ће бити тражени круг k.

• Конструисати круг који садржи дату тачку А и додирује дату  праву р1 и дати  круг O1.

 
Нека је круг k тражени круг.При инверзији у односу на круг m ( А, r ), где је r произвољна дуж,правој одговара неки  круг р1', кругу O1одговара неки круг O1', а траженом кругу k права k' која додирује кругове р1' и O1'.
Дакле, потребно је конструисати најпре р1 и O1' инверзне линијама р1 и O1  у односу на круг m ( А, r ),затим заједничку тангенту k' кругова р1' и O1',(у општем  случају их има четири) и на крају круг k инверзан правој k' у односу на круг инверзије m ( А, r ) (сл.10.).
Можемо закључити,да у решавању овог проблема није било од значаја да ли  су р1 и O1 баш права и круг, већ да су њихове инверзне слике р1' и O1'
кругови.Међутим, р1' и O1' би били баш кругови и у случају да су р1 и O1  две праве и А   р1 , O1.

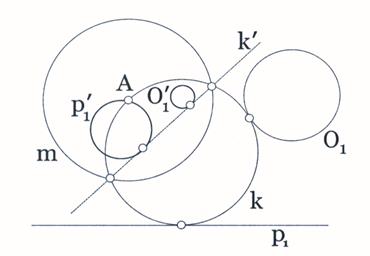
Слика 10.
ДРУГИ НАЧИН: Дати су круг O1 права р1  и тачка А која није ни на правој р1ни на кругу  O1 .(слика 11.)

 19 

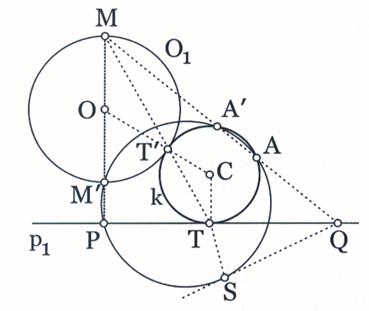
Слика 11.
 Анализа: Круг O1 и праву р1 можемо за инверзне фигуре и то: праву р1  као инверзију круга O1,у односу на крајњу тачку М пречника ММ' нормалног на праву  р1.Модуо инверзије је тада ·= k . Нека је тачка А' инверзна тачки А.Онда је ·= k.Према томе, тачку А', инверзну тачки А,добијамо  из једнакости:
·  = ·.  (1)
Ова једнакост тврди да су четири тачке  М' , Р , А , А' на истом  кругу.То је круг који пролази кроз три од ових тачака:Р, М', А. Овај круг пресеца праву МА у тачки А'.
Тражени круг треба да пролази кроз тачку А и треба да додирује праву р1 у тачки Т,а круг у тачки Т '. Пошто ОМТ = СТТ ',то је тачка Т ' инверзија тачке Т,у односу на тачку М.Инверзија круга са центром у С,биће круг који пролази кроз Т и Т ' и кроз А',а то значи да је тај круг сам себи инверзан.У исто време, круг АТТ ' припада прамену кругова,који је одређен кругом РМ'А и правом МА као потенцијалном осом.

 Конструкција: Конструисати круг РМ'А који пресеца МА у тачки А' инверзији тачке А у односу на Р (једнакост (1)). Тачка у којој тражени круг додирује праву р1 добија се ако се из тачке Q повуче тангента QS на круг РМ'А и пренесе QS = QТ.Симетрала дужи АА' и нормала повучена у тачки Т на праву родређује центар (С) траженог круга. ■

Закључујемо да се четврти и шести Аполонијев проблем решавају на исти начин као и пети.Осми,девети и десети Аполонијев проблем своде се редом на четврти ,пети и шести.

 5. МАСКЕРОНИЈЕВЕ КОНСТРУКЦИЈЕ

 Инверзија има пуно примена код тврђења која приказују  разне односе међу правама, круговима као и односе међу правама Једна од  примена јесте и при Маскеронијевим конструкцијана или друкчије званим  конструкцијама само шестаром .

 Под конструкцијом се у класичној еуклидској геометрији подразумева низ операција помоћу шестара и лењира,које се могу сврстати у једну од следећих  пет група:

1. Одређивање праве кроз две задате тачке,

2. Одређивање пресека две задате тачке,

3. Одређивање круга са задатим центром и полупречником,

4. Одређивање пресека две праве и датог круга, и

5. Одређивање пресека два дата круга.

 Каже се да се конструкције изводе уз помоћ лењира и шестара,јер ове механичке направе у идеалном случају омогућавају извођење ових корака.Поставља се питање да ли је могуће неку од ових справа изоставити из процеса конструкције. Јасно је да није могуће само лењиром конструисати круг илисамо шестаром праву. Ипак,може се усвојити договор да је у првом случају круг конструисан ако му је познат центар и једна тачка, а да је у другом случају права конструисана ако су јој дате две тачке.При томе се,наравно,захтева да се над сваким на тај начин "добијеним" кругом, односно правом,могу даље вршити операције 1-5.

 Литература
 
 1. З.Лучић, Еуклидска и хиперболичка геометрија, Графити и Математички факултет, Београд,1994.

 2. М.Станковић, Основи геометрије, Природно-математички факултет, Ниш, 2006.

 3. А.И.Фетисов, О еуклидској и нееуклидским геометријама, Школска Књига, Загреб, 1981.

 4. Р.Тошић, В.Петровић, Проблеми из геометрије, ПМФ, Нови Сад,1995.

 5. В.Ј.Павковић, Инверзија у равни и њене примене, Питагорини материјали за младе математичаре, ДММ „Питагора“,Бели Манастир,1989.

 6. З.Михајловић, О трансформацијама у елементарној геометрији,  Математичка библиотека,1959.

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi