Euklid je bio antički matematičar poznat po svojim delima „Elementi“, „Data“, „Optika“ i algoritmu za izračunavanje najvećeg zajedničkog delioca (NZD) koji je po njemu nazvan Euklidov algoritam.
Živeo je u periodu od 330 - 275.god. p.n.e. Bio je poznati grčki matematičar iz Atine. Živeo je i radio u Aleksandriji gde je stvorio matematičku školu.

Napisao je brojna dela, od kojih neka nisu sačuvana i poznata su samo po naslovu. Sačuvana dela su:

Nastanak ideje o definisanju prostora

U grčkoj geometriji nije bilo eksplicitnog pojma prostora. Međutim, implicitno, pojam prostora je postojao kao epifenomen, kao okvir u kojem se geometrijski objekti nalaze. U savremenoj geometriji imamo njegovu simboličku kodifikaciju kao skup svih uredjenih trojki realnih brojeva. Posmatranje spoljašnjeg prostora kao prebivališta realnih stvari i doživljavanje mentalnog prostora kao prebivališta zamišnenih stvari nisu naučene sposobnosti, već prirodni darovi ljudskih bića. Tako, mi nikada ne tražimo od naših đaka objašnjenje šta je prostor, niti pokušavamo da ga njima sugerišemo.
U matematici, skup tačaka koje su u jedan-jedan korespondenciji sa svim uređenim trojkama realnih brojeva, naziva se trodimenzionalni prostor. Tri broja x, y, z u trojci (x, y, z) koja je pridružena nekoj tački A, nazivaju se njenim koordinatama. Podskupovi prostora koji korespondiraju podskupovima

(x, 0, 0) : x Є R, (0, y, 0) : y Є R, (0, 0, z) : z Є R

skupa trojki, nazivaju se x-osa, y-osa i z-osa. Za dve tačke A(x1, y1, z1) i B(x2, y2, z2), odsečak AB se definiše kao skup tačaka koji korespondira sledećem podskupu trojki

(λx1 + (1 − λ)x2, λy1 + (1 − λ)y2, λz1 + (1 − λ)z2) : λ Є[0, 1] .

Onda se dužina ovog odsečka, a time i rastojanje tačaka A i B, definiše kao broj

d(A,B) = _(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2.

Izostavljamo dodatne detalje koji su poznati čitaocu iz kursa analitičke geometrije i koji se obično uče putem vizuelizacije. Crtež koji predstavlja koordinatni sistem - tri prave koje stoje normalno jedna na drugu, jeste ono čime počinju ovakve lekcije iz analitičke geometrije, pri čemu su tri uzajamno normalne ivice zidova jedne sobe veoma dobra materijalizacija jednog takvog skupa trojki, nazivaju se x-osa, y-osa i z-osa. Za dve tačke

A(x1, y1, z1) i

B(x2, y2, z2), odseqak AB se definiše kao skup tačaka koji korespondira sledećem podskupu trojki

š (λx1 + (1 − λ)x2, λy1 + (1 − λ)y2, λz1 + (1 − λ)z2) : λ Є [0, 1] ć.

Onda se dužina ovog odsečka, a time i rastojanje tačaka A i B, definiše kao broj

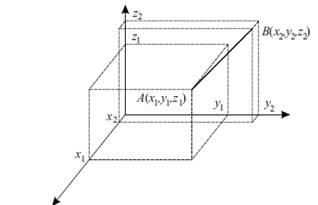
Euklidov prostor

Euklidov prostor je prostor čija se svojstva opisuju aksiomama apsolutne geometrije i Euklidovim postulatom (aksiomom) o paralelnim pravama.
Opštije rečeno, Euklidov prostor se naziva n-dimenzionalni metrički prostor, u kojem je moguće uvesti Dekartov koordinatni sistem i tada se metrika definiše na sledeći način: rastojanje između tačke M sa koordinatama (x1,x2,...,xn) i tačke M'(x_1',x_2',...,x_n') izračunava se po formuli:
$\rho =\overline{MM'}=\sqrt{(x_1-x_1')^2+(x_2-x_2')^2+...+(x_n-x_n')^2}.$

DEFINICIJA I OPŠTA SVOJSTVA IZOMETRIJSKIH TRANSFORMACIJA PROSTORA

Aksiome podudarnosti omogućavaju da u geometriji prostora definišemo posebnu klasu transformacija koju nazivamo izometrijskim transformacijama.

Definicija: Svaku bijekciju I prostora na sebe nazivamo izometrijskom transformacijom ili izometrijom ako je slika svakog para (A,B) tačaka njemu podudaran par tačaka (I(A), I(B)). Iz definicije neposredno sledi da je identičnost izometrijska transformacija budući da za svake dve tačke A,B prostora važi relacija (A,B) ± (A,B).

Teorema: Skup svih izometrija predstavlja grupu u odnosu na proizvod transformacija:

Dokaz: Neka su I1 i I2 bilo koje dve izometrije prostora i A i B proizvoljne tačke tog prostora. Neka se tačke A i B izometrijom I1 preslikavaju redom u tačke A1 i B1, a tačke A1 i B1 izometrijom I2 redom u tačke A2 i B2. Tada će biti:

I2I1(A) = I2(A1) = A2, I2I1(B) = I2(B1) = B2 i (A, B) ± (A1, B1), (A1, B1) ± (A2, B2)

pa je i (A, B) ± (A2, B2). Stoga je i kompozicija I2I1 izometrijska transformacija prostora.

Iz (A,B) ± (A1,B1) sledi da je i (A1,B1) ± (A,B) jer je relacija podudarnosti parova tačaka simetrična, pa je i inverzna transformacija I1-1 takođe izometrijska transformacija.

U narednoj teoremi navodimo uslove pod kojima je izometrija prostora jednoznačno određena:

Teorema: Ako su A,B,C,D četiri nekomplanarne tačke, a A',B',C',D' četiri tačke prostora takve da je (A,B,C,D) ± (A',B',C',D') tada postoji jedinstvena izometrija prostora u kojoj se tačke A,B,C,D preslikavaju, redom, na A',B',C',D'

Posledica: Ako izometrijska transformacija prostora poseduje četiri nekomplementarne invarijantne tačke, ona predstavlja koincidenciju.

Poznavajući aksiome podudarnosti lako se može dokazati sledeće tvrđenje:

Teorema : Tačke sa iste strane neke ravni izometrijom se preslikavaju na tačke sa iste strane slike te ravni, a tačke sa raznih strana ravni u tačke sa raznih strana slike te ravni.
Takođe, izometrijom I se prava preslikava na pravu, poluprava sa temenom O na polupravu sa temenom I(O), a duž AB na duž A'B', gde je A'=I(A) i B'=I(B). Slično, ravan se preslikava na ravan, poluravan sa ivicom s na poluravan sa ivicom I(s), a konveksan ugao pq na koveksan ugao p'q', gde je p'=I(p) i q'=I(q). Zatim poligonska linija se preslikava na poligonsku liniju, oblast na oblast, konveksan lik na konveksan lik, poligon na poligon, poligonska površ na poligonsku površ, rogljasta površ na rogljastu površ, rogalj na rogalj, poliederska površ na poliedersku površ i poliedar na poliedar.

ORIJENTACIJA PROSTORA

Da bismo opisali sve izometrije prostora neophodno je nejpre upoznati se sa orijentacijom prostora. Kako je prostor određen sa četiri nekomplanarne tačke, orijentaciju prostora možemo posmatrati uz pomoć orijentacije tetraedra koji je određen sa te četiri tačke.

Tetraedar A1A2A3A4 čija su temena uređene četvorke tačaka (A1,A2,A3,A4) zvaćemo orijentisanim. Ako je A2=B1, A3=B2, A4=B3, orijentisane tetraedre A1A2A3A4 i B1B2B3B4 zovemo nadovezanim. Lanac orijentisanih tetraedara je konačan niz orijentisanih tetraedara u kome su svaka dva uzastopna člana nadovezana.

Početak lanca je njegov prvi član, a kraj poslednji član lanca. Lanac je zatvoren ako su istovetni njegov početak i kraj. Lanac povezuje tetraedre t i t' ako je t njegov početak, a t' njegov kraj. Par nadovezanih orijentisanih tetraedara A1A2A3A4 i A2A3A4A5 zvaćemo preorijentacijom ako su tačke A1 i A5 sa iste strane ravni A2A3A4 Parnost lanca je broj preorijentacja među parovima uzastopnih tetraedara u tome lancu. Orijentisane tetraedre t i t' zovemo istosmernim (pišemo t ® t'), ako je svaki lanac koji ih povezuje paran, u suprotnom ih zovemo suprotnosmernim (pišemo t « t').

KLASIFIKACIJA IZOMETRIJSKIH TRANSFORMACIJA PROSTORA

Izvršimo klasifikaciju svih izometrijskih transformacija prostora. Na osnovu teoreme svaka direktna izometrija prostora može se izraziti kao proizvod dveju osnih simetrija prostora Sm i Sn. U zavisnosti od međusobnog položaja osa m i n razlikujemo nekoliko mogućnosti:

a) ako ose m i n pripadaju ravni p, a n i m su ravni koje sadrže i upravne su na p.
Tada je
I = SmSn = SvSpSpSm = SvSm.

1. Ako su m i n istovetne ravni n i m će biti istovetne pa će kompozicija SnSm biti identičnost.
2. Ako se m i n seku i ravni n i m se seku duž prave koja je u njihovoj presečnoj tački upravna na p, pa je I osna rotacija prostora.
3. Ako su m i n međusobno paralelne i n i m će biti paralelne pa je I translacija prostora

4. Ako su m i n mimoilzne prave, tada je na osnovu teoreme 10.2. izometrija I zavojno kretanje prostora.

Ako je I neka indirektna izometrija tada postoji tačka P tog prostora koja nije invarijantna u transformaciji I. Neka je I(P) = P' i neka je p medijalna ravan duži PP'. U kompoziciji SpI tačka P je invarijantna, pa kako je ta kompozicija direktna izometrija prostora ona će biti ili identičnost ili osna rotacija.

Ako je SpI identičnost, I je ravanska refleksija.

Pretpostavimo da je SpI = Rs,w. Prava s ne pripada ravni p, jer bi u suprotnom I bila ravanska refleksija. Obeležimo sa m ravan koja sadrži pravu s, a upravna je na p, a sa n ravan takvu da je Rs,w = SmSn. Tada je I = SpSmSn. Tada je I = SpSmSn = SpSn, gde je p presek međusobno upravnih ravni p i m. Prava p ne pripada n jer bi u suprotnom izometrija I bila refleksija. Obeležimo sa s ravan koja sadrži p i upravna je na n, a sa t ravan koja sadrži p i upravna je na s. Tada je: [ 3. str. 189.]

I = SpSn = StSdSn = SdStSn.

S obzirom na međusobni položaj ravni n i t upravnih na s razlikujemo sledeće slučajeve: [1 str. 201.]

1. Ako se ravni n i t seku I je po definiciji rotaciona refleksija prostora
2. Ako su ravni n i t međusobno paralelne I je po definiciji klizajuća refleksija prostora.

Time smo dokazali sledeće tvrđenje:

Teorema: Ako nije identičnost, direktna izometrija euklidskog prostora je ili rotacija, ili translacija, ili zavojno kretanje. Ako nije ravanska refleksija, indirektna izometrija euklidskog prostora je ili rotaciona ili klizajuća refleksija.

DIREKTNE I INDIREKTNE IZOMETRIJE PROSTORA

Teorema: Izometrijom prostora se istosmerni tetraedri preslikavaju na istosmerne tetraedre, a suprotnosmerni na suprotnosmerne tetraedre.

Dokaz: Neka je I izometrija kojom se tretraedar ABCD preslikava na tetraedar A'B'C'D'. Ako je PQRS proizvoljan tetraedar i P'Q'R'S' njegova slika u izometriji I, a L lanac orijentisanih tetraedara koji povezuje tetraedre ABCD i PQRS, a tada slika svakog od orijentisanih tetraedara toga lanca orijentisani tetraedar, pa je slika toga lanca neki lanac L'. Kako se izometrijom tačke sa iste strane neke ravni slikaju u tačke sa iste strane slike te ravni, a tačke sa raznih strana ravni u tačke sa raznih strana slike te ravni, broj preorijentacija među parovima uzastopnih orijentisanih tetraedara lanaca L i L' će biti isti, pa su ti lanci iste parnosti. Odatle sledi da su tetraedri ABCD i PQRS istosmerni ako i samo ako su njihove slike A'B'C'D' i P'Q'R'S' u izometriji I istosmerni orijentisani tetraedri.

Iz ovog tvrđenja neposredno sledi da postoje dve izometrije prostora: direktne izometrije, koje ne menjaju orijentaciju prostora i indirektne izometrije koje je menjaju. Da bi smo ustanovili da li je neka izometrija prostora direktna ili indirektna dovoljno je utvrditi da li dve odgovarajuće četvorke nekomplanarnih tačaka određuju istosmerne ili suprotnosmerne tetraedre. Iz teoreme sledi da je direktna (indirektna) izometrija prostora jednoznačno određena ako su zadata tri para odgovarajućih nekolinearnih tačaka. Specijalno, direktna izometrija koja ima tri invarijantne nekolinearne tačke predstavlja koincidenciju. Kompozicija dveju direktnih ili dveju indirektnih izometrija prostora uvek predstavlja direktnu izometriju tog prostora, dok kompozicija sastavljena iz jedne direktne i jedne indirektne izometrije uvek predstavlja indirektnu izometriju prostora.

Sledeće teoreme nam omogućavaju uvođenje pojma orijentacije prostora:

Teorema: Za svaka dva orijentisana tetraedra t i t' postoji lanac L koji ih povezuje.

Teorema: Zatvoreni lanci su parni.

Teorema: Lanci koji imaju zajednički početak i kraj su iste parnosti.

Teorema: Relacija istosmernosti orijentisanih tetraedara je relacija ekvilalencije koja familiju orijentisanih tetraedara razlaže na dve klase ekvivalencije.
Klase ekvivalencije na koje relacija istosmernosti razlaže skup orijentisanih tetraedara zovemo smerovima prostora.

RAVANSKA REFLEKSIJA PROSTORA

Teorema nam kazuje da postoji izometrija prostora koja ostavlja invarijantnim tri nekolinearne tačke, tj. izometrija prostora koja ostavlja invarijantnim sve tačke jedne ravni. Tu izometriju prostora zovemo ravanskom refleksijom.

Definicija: Ravanskom refleksijom ili ravanskom simetrijom prostora sa osnovom p zovemo neidentičku izometriju prostora kojoj je svaka tačka ravni p invarijantna. Obeležavamo je sa Sp. Ravan p zovemo osnovom ili ravni refleksije.

Važno je napomenuti da ravanska refleksija van ravni p nema invarijantnih tačaka.

Neka su A,B,C tri nekolinearne tačke ravni p i neka je X' slika proizvoljne tačke X u ravanskoj refleksiji Sp. Tada je:

AX ± AX', BX ± BX', CX ± CX'.
Odatle sledi da tačke A,B,C pripadaju meridijalnoj ravni p' duži XX'. Kako su A,B,C nekolinearnre tačke, one određuju jednu i samo jednu ravan, pa je p=p'. Ovim smo dokazali sledeću teoremu.

Teorema: Ako se ravaskom refleksijom Sp tačka X preslikava u tačku X' tada je ravan p medijalna ravan duži XX'.

Navedimo još nekoliko važnih svojstava ravanskih refleksija.

Teorema: Ravanska refleksija prostora je indirektna izometrija.

Dokaz: Neka je Sp neka ravanska refleksija i neka su A,B,C tri nekolinearne tačke ravni p. Sa D' obeležimo tačku takvu da je D' = Sp(D). Tada je D ¹ D' i p je medijana ravan duži DD'. Stoga su tačke D i D' sa raznih strana ravni p pa su odgovarajući tetraedri ABCD i ABCD' suprotosmerni što znači da je ravanska refleksija Sp indirektna izometrija
prostora.

Teorema: Ravanska refleksija prostora je involuciona transformacija.s

Dokaz: Neka je X proizvoljna tačka prostora i neka je Sp neka ravanska refleksija tog prostora. Obeležićemo sa X' i X'' tačke takve da je Sp(X) = X' i Sp(X') = X''. Ako X Î p tada je X = X' i X' = X'', pa je i X = X''. Ako X Ï p tada je X ¹ X' i X' ¹ X'', pa je osnova p ravanske refleksije Sp medijalna ravan svake od duži XX' i X'X''. Tada je X = X''. Ovim smo dokazali da je Sp2 = e (sa e označavamo identičnost), pa je Sp involuciona transformacija prostora.

Teorema: Ako indirektna izometrija prostora poseduje dve razne invarijantne tačke tada ona predstavlja ravansku refleksiju i pri tom osnova ravanske refleksije sadrži ove tačke.

Dokaz: Neka je indirektna izometrija prostora i neka su A i B dve proizvoljne tačke tog prostora. Kako je I indirektna, a e direktna izometrija prostora, biće I ¹ e. Stoga postoji tačka P takva je da je I(P) = P' i P ¹ P'. Pri tom je (P,A) ¹ (P', A) i (P,B) ¹ (P', B) i tačke A,B se nalaze u medijalnoj ravni p duži PP'. Kako su Sp i I indirektne izometrije kompozicija SpI predstavlja direktnu izometriju prostora koja ostavlja invarijantnim tačke A,B,P, pa ona predstavlja konicidenciju. Stoga je
SpI = e, pa je I = Sp.

Teorema: Neka su Sa i Sb dve ravanske refleksije sa raznim osnovama. Tačka X je invarijantna u kompoziciji SaSb ako i samo ako pripada obema osnovama tih refleksija.

Dokaz: Ako X pripada osnovama a i b ona će biti invarijantna u svakoj od tih refleksija, dakle i u njihovoj kompoziciji.

Obrnuto, neka je SaSb(X) = X i pretpostavimo da je Sb(X) = Y, pri čemu je X ¹ Y. Tada mora biti Sa(Y) = X. Odatle sledi da su a i b dve razne medijalne ravni duži XY što je nemoguće, pa je X = Y.

Teorema: Ako je Sp neka ravanska refleksija prostora i I bilo koja izometrija tog prostora, a p' ravan koja u izometriji I odgovara ravni p. Tada je ISpI-1 = Sp'.

Dokaz: Neka je P proizvoljna tačka ravni p. Kako je I(p) = p' tački P će u izometriji I odgovarati tačka P' = I(P) i P' Î p'. Odatle neposredno sledi da je SpI-1(P') = I-1(P'), pa je ISpI-1(P') = II-1(P') = (P').

Dakle u kompoziciji ISpI-1 svaka tačka ravni p je invarijantna, pa kako je ta
kompozicija indirektna izometrija ona će biti ravanska refleksija Sp'.

Teorema: Dve ravanske refleksije prostora komutiraju ako i samo ako su im osnove istovetne ili međusobno upravne ravni.

Dokaz:Neka je SbSa = SaSb, tj. SbSaSb = Sa (1). Ako je a' = Sb(a) iz prethodne teoreme sledi da je SbSaSb = Sa'. (2). Iz jednakosti (1) i (2) sledi da je Sa= Sa', pa je a = a', tj. a = Sb(a). Odatle zaključujemo da su ravni a i b istovetne ili međusobno upravne.
Obrnuto, ako su osnove a i b istovetne ili međusobno upravne ravni biće Sb(a) = a, pa je na osnovu prethodne teoreme SbSaSb = Sa, tj. SbSa = SaSb.
Sledeće teorema je jedna od najznačajnijih teorema ove oblasti. Formulaciju i dokaz ove teoreme u potpunosti je preuzet iz knjige profesora Zorana Lučića „Osnovi geometrije”.

Teorema: Svaka izometrija prostora može se predstaviti kao kompozicija najviše četiri ravanske refleksije prostora.

Dokaz: Neka je I proizvoljna izometrija prostora i A,B,C,D četiri nekoplanarne tačke, a A1,B1,C1,D1, redom, slike tih tačaka u izometriji I.

Ako je A = A1, B = B1, C = C1, D = D1, I je identičnost pa, ako je p proizvoljna ravan, biće I = SpSp. Pretpostavimo stoga da nisu sve tačke A,B,C,D invarijantne u izometriji I već da se bar jedna od njih, na primer A, tom izometrijom preslikava u tačku koja je od nje različita. Ako je S1 refleksija kojom se A i A1 preslikavaju jedna na drugu, u kompoziciji S1I će tačka A biti invarijantna. Ako su u toj kompoziciji i B,C,D invarijantne tačke, biće I = S1.

Pretpostavimo da u izometriji S1I bar jedna od tačaka B,C,D na primer B, nije invarijantna već da se preslikava na B2, a C i D redom na C2 i D2, i sa S2 obeležimo refleksiju kojom se B i B2 preslikavaju jedna na drugu. Tada je
(A,B) ± (A1, B1) ± (A,B2),

pa tačka A pripada osnovi p2 refleksije S2. Stoga su u kompoziciji S1S2I tačke A i B invarijantne. Ako su invarijantne i C i D, ta kompozicija je identičnost pa je tada I = S1S2.

Pretpostavimo da u izometriji S1S2I tačka C nije invarijantna već da se preslikava na C3, a D na D3, i sa S3 obeležimo refleksiju kojom se C i C3 preslikavaju na drugu. Tada je

(A,C) ± (A1,C1) ± (A,C2) ± (A,C3) i (B,C) ± (B1,C1) ± (B2,C2) ± (B,C3),

pa tačke A i B pripadaju osnovi p3 refleksije S3. Stoga su tačke A,B,C invarijantne u kompoziciji S3S2S1I. Ako je invarijantna i tačka D, ta kompozicija je identičnost pa je tada
I = S1S2S3.

Pretpostavimo da u izometriji S3S2S1I tačka D nije invarijantna već da se preslikava na D4, i sa S4 obeležimo refleksiju kojom se D i D4 preslikavaju jedna na drugu. Tada je
(A,D) ± (A1,D1) ± (A,D2) ± (A,D3) ± (A,D4),
(B,D) ± (B1,D1) ± (B2,D2) ± (B,D3) ± (B,D4),
(C,D) ± (C1,D1) ± (C2,D2) ± (C3,D3) ± (C,D4),

pa tačke A,B,C pripadaju osnovi p4 refleksije S4. Stoga su tačke A,B,C,D invarijantne u kompoziciji S4S3S2S1I. Dakle, ta kompozicija je identičnost pa je tada I = S1S2S3S4.

OSNA ROTACIJA I OSNA SIMETRIJA PROSTORA

Definicija: Neka su Sa i Sb dve ravanske refleksije euklidskog prostora kojima se osnove a i b seku duž prave s. Osnom rotacijom prostora oko prave s za ugao w, nazivamo transformaciju Rs,w određenu relacijom Rs,w = SbSa. Pravu s zovemo osom, a ugao w (koji je jednak dvostrukom uglu koji zahvataju ravni a i b) zovemo uglom osne rotacije Rs,w. Ako su ravni a i b međusobno upravne takvu rotaciju nazivamo osnom simetrijom prostora i obeležavamo sa Ss.
Kako se osna rotacija i osna simetrija dobijaju kao kompozicija dveju indirektnih izometrija, one predstavljaju direktnu izometrijsku transformaciju.[1, str. 257.]

Teorema: (Dalamberova): Svaka direktna izometrija prostora koja ima najmanje jednu invarijantnu tačku je identičnost ili osna rotacija.

Dokaz: Neka direktna izometrija I istavlja invarijantnom tačku O. Tada postoji tačka X čija je slika, Y = I(X), od nje različita. Tada postoji medijalna ravan a duži XY. Tačke O i X će biti invarijantne u kompoziciji SaI, pa je na osnovu teoreme 4.4, SaI = Sb, tj. I = SaSb, pri čemu b sadrži tačke O i X. Kako X pripada ravni b, ali ne i ravni a, te dve ravni su različite i seku se, jer obe sadrže tačku O. Dakle, I predstvlja osnu rotaciju prostora.
Iz prethodne teoreme neposredno sledi znamenita Ojlerova teorema o proizvodu rotacija, prema kojoj je kompozicija dveju osnih rotacija prostora čije se ose seku, opet osna rotacija.

Teorema: Osna rotacija Rs,w i ravanska refleksija Sp euklidskog prostora su komutativne transformacije ako i samo ako je prava s upravna na ravni p.

Dokaz: Neka je SpRs,w = Rs,wSp. Taka je SpRs,wSp.= Rs,w (1). Neka je Rs,w= SnSm. Ravni n i m se seku duž prave s, pod uglom Ð(m,n) = w/2. Obeležimo sa n' i m' ravni takve da je Sp(m) = m' i Sp(n) = n' seku duž prave s pod uglom Ð(m',n') = w'/2. Primenom teoreme 4.5 nalazimo da je

SpRs,wSp = Sp(SnSm)Sp = (SpSnSp)(SpSmSp) = Sn'Sm' = Rs',w' (2)
Iz (1) i (2) sledi Rs,w = Rs',w'. Zbog toga su ose s i s' istovetne, a orijentisani uglovi w i w' podudarni i istosmerni, a to je moguće samo ako je prava s upravna na ravni p.

Pretpostavimo sada da je prava s upravna na ravni p. Obeležimo sa s' pravu koja je u ravanskoj refleksiji Sp odgovara pravoj s, a sa w' ugao koji u toj refleksiji odgovara uglu w. Tada će prave s i s' biti istovetne, a uglovi w i w' podudarni i istosmerni, pa je Rs,w = Rs',w'. Iz (2) nalazimo da je

SpRs,w= (SpRs,wSp)Sp = Rs',w'Sp+ = Rs,wSp
Naravno, teorema važi i ako je rotacija Rs,w, osna refleksija Ss.
Lako se dokazuje da je osna rotacija involuciona transformacija.

Primer: Dokazati da je kompozicija sastavljena iz tri osne refleksije SpSqSr prostora kojima su ose upravne na nekoj ravni p, predstavlja takođe osnu refleksiju kojoj je osa upravna na ravni p.

Rešenje: Neka ravni a, b, g sadrže redom prave p, q, r i međusobno su paralelne i neka su a', b', g' ravni takve da je Sp = SaSa', Sq = SbSb', Sr = SgSg'. Ravni a', b', g' su takođe međusobno paralelne i upravne na svakoj od ravni a, b, g. Ravni a, b, g pripadaju nekom pramenu paralelnih ravni, pa je SgSbSa= Sd, gde jed takođe ravan tog pramena. Slično a', b', g', pripadaju nekom drugom pramenu ravni, pa je Sg'Sb'Sa' = Sd', gde je d' ravan tog pramena, pa je stoga d' upravna na d. Tada je:

SrSqSp = (SgSg')(SbSb')(SaSa') = SgSbSgSb'SaSa' =
= SgSbSg'SaSb'Sa' = (SgSbSa)(Sg'Sb'Sa') = SdSd' = Sd,
pri čemu je d upravna na p.

ROTACIONA REFLEKSIJA I CENTRALNA SIMETRIJA PROSTORA

Definicija: Rotacionom refleksijom prostora nazivamo kompoziciju triju ravanskih Sp, Sa, Sb, pri čemu se ravni a i b seku duž neke prave s koja je upravna na ravni p i obeležavamo je sa Rp;s,w. Dakle, Rp;s,w = SpSaSb. Ravan p zovemo osnovom, pravu s osom, a ugao w (koji zahvataju ravni a i b) uglom rotacione refleksije Rp;s,w. Ako su ravni a i b međusobno upravne rotacionu refleksiju Rp;s,w zovemo centralnom simetrijom prostora i obeležavamo je sa So, gde je O tačka prodora prave s kroz ravan p.
Iz definicije direktno proizilazi da su rotaciona refleksija i centralna simetrija indirektne izometrijske transformacije.

Teorema: Svaka indirektna izometrija prostora sa jedinstvenom invarijantnom tačkom je rotaiciona refleksija.

Dokaz: Neka je I indirektna izometrija prostora i neka se njome tačka P slika u neku drugu tačku Q. Ako je O jedina invarijantna tačka transformacije I, biće (O,P) ± (O,Q), pa tačka O pripada medijalnoj ravni a duži PQ. Kompozicija SaI je direktna izometrijska transformacija u kojoj su tačke P i Q invarijantne. Po teoremi 6.1. ova izometrija predstavlja ili identičnost ili osnu roraciju Rs,w čija osa s sadrži tačke O i P. Ako bi izometrija SaI bila identičnost I bi bila ravanska refleksija, pa bi pored tačke O posedovala još invarijantnih tačaka. [3, str. 185.]

Zbog toga je SaI = Rs,w. Kako tačka O pripada pravoj s i ravni a, a tačka P samo pravoj s, prava s prodire ravan a u tački O. Ako je uz to s upravna na a, I će po definiciji biti rotaciona refleksija. Ako s nije upravna na a obeležimo sa b ravan koja sadrži s i upravna je na a, a sa g ravan takvu da je Rs,w = SbSg. Ako je p presečena prava ravni a i b biće
I = SaSbSg = SpSg

Neka je d ravan koja sadrži p i upravna je na g, a q ravan koja sadrži p i upravna je na d. Tada je Sp = SdSq, pa kako su ravni g i q upravne na d i sadrže tačku O biće

I = SdSqSg = SdRd;t,j.
Teorema: Svaka direktna izometrija prostora može se izraziti kao kompozicija dve osne simetrije.

Dokaz: Ako je direktna izometrija prostora identičnost, ona se može predstaviti kao kompozicija I = SpSp, gde je p bilo koja prava. Pretpostavimo da I nije identičnost. Tada postoji tačka P i tačka Q takva da je I(P) = Q i P ¹ Q. Neka je a medijalna ravan duži PQ. Kompozicija SaI je indirektna izometrija sa invarijantnom tačkom P, pa je ona po prethodnoj teoremi ravanska ili rotaciona refleksija prostora.

Ako je SaI = Sb i ako je p ravan koja je upravna na a i na b, a p i q presečne prave ravni p sa ravnima a i b tada je
I = SaSb = SaSpSpSb = SpSq.
Ako je SaI = Rd;s,w i ako je b ravan koja sadrži s i upravna je na a, g ravan takva da je Rs,w = SbSg a p i q presečene prave, redom parova ravni a i b,g i d, tada je
I = SaRd;s,w = SaSbSgSd = SpSq.

Teorema: Kompozicija triju centralnih simetrija prostora predstavlja takođe centralnu simetriju tog prostora.

Dokaz: Neka su date tri centralne simetrije SA, SB, SC prostora. Ako je pri tome A = B ili B = C, tada neposredno sledi da kompozicija SCSBSA predstavlja takođe centralnu simetriju. Neka je A ¹ B ¹ C i neka je p ravan koja sadrži tačke A, B, C i a, b, c prave koje su u tim tačkama upravne na p. Tada je

SCSBSA = (SpSc)(SbSp)(SpSa) = Sp(ScSbSa)

Kako su prave a, b, i c upravne na p kompozicija ScSbSa predstavlja osnu simetriju Sd kojoj je osa d upravna na ravni p (primer 6.1.). Neka je D prodorna tačka prave d na ravni p. Tada je
SCSBSA = Sp(ScSbSa) = SpSd = SD.

Teorema. (Šal-Hjelmsleva): Središta duži koje spajaju odgovarajuće tačke neke indirektne izometrije prostora pripadaju jednoj ravni.

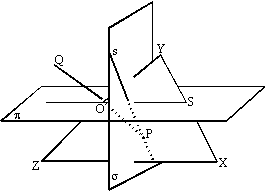
Dokaz: Neka je P tačka prostora koja se indirektnom izometrijom I slika u tačku Q i neka je O središte duži PQ. Kompozicija SoI je direktna izometrija u kojoj je tačka P invarijantna, pa je na osnovu Dalamberove teoreme ona ili identičnost ili osna rotacija Rs,w, pri čemu tačka P pripada pravoj s.

Ako je kompozicija SoI identičnost biće I = So, pa dokaz sledi neposredno.

Ako nije, obeležimo sa p ravan koja sadrži O i upravna je na s, sa X proizvoljnu tačku prostora različitu od P, a sa Y sliku tačke Y u transformaciji I. Dokažimo da središte S duži XY pripada ravni p. Tada važi, SoI = Rs,w i I(X) = Y. Ako je So(Y) = Z, biće Rs,w(X) = SoI (X) = So(Y) = Z, pa medijalna ravan s duž XZ sadrži pravu s. Prava OS je upravna na s, pa je upravna i na pravoj s koja joj pripada. Odatle sledi tačka S pripada ravni p.

Napomenimo još na kraju da se prava koja sadrži centar centralne simetrije slika tom simetrijom u sebe, a prava koja ne sadži centar simetrije u njoj paralenu pravu. Takođe, ravan koja sadrži centar centralne simetrije tom simetrijom se slika u sebe, a ravan koja ne sadži centar simetrije se slika u njoj paralelnu ravan.

LITERATURA

1. Dragomir Lopandić, Geometrija, Naučna knjiga, Beograd 1980.

2. Zoran Lučić, Euklidska i hiperbolička geometrija, Matematički fakultet, Beograd 1994.

3. Dragomir Lopandić Geometrija (Naučna knjiga ,Beograd, 1988.)

4. www.wikipedia.com

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi