Greške velikih matematičara

 „Jama je duboka 50 stopa. Lav se popne 1/7 stope svakog dana i zatim sklizne nazad 1/9 stope svake noći. Koliko će mu dana biti potrebno da izađe iz jame?”

Fibonači je pošao od 63,broja koji je deljiv sa 7 i sa 9, i našao da će se za 63 dana lav popeti 9 stopa i skliznuti 7 stopa. Dakle lav napreduje 2/63 stope svakog dana i, koristeći proporciju, on je izračunao da će lavu biti potrebno (50 : 2) x 63 = 1575 dana da se popne 50 stopa i stigne do vrha jame.
Fibonačijev odgovor je pogrešan; on je upao u naivnu zamku kao i mnogi amateri. Očigledno, na kraju 1571. dana će bitisamo 8/63 stopa do vrha i, sledećeg dana, će stići do vrha (1/7 > 8/63). A kad se jednom dokopa izlaza, lav neće, kao prethodnih danam skliznuti natrag za 1/9 stope.

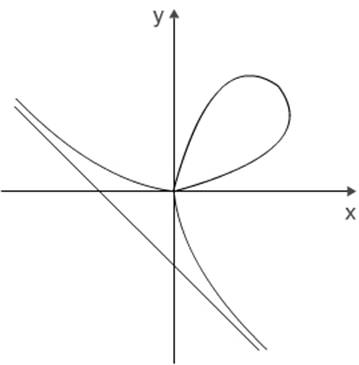
Čuveni francuski matematičar i filozof Rene Dekart (1596-1650) u svom pismu koje je 1638. poslao francuskom matematičaru Marenu Mersenu (Marin Mersenne, 1588-1648) a ovaj proslediio Pjeru Fermau, dao je pogrešnu sliku krive x3 +y3 = axy, poznatu kao Dekartov list. On je nameravao da pokaže da se Fermaov metod tangenti ne može primeniti na ovu krivu, ali nije ispravno razmotrio beskonačne grane krive. Kristijan Hajgens je 1692. dao tačnu sliku krive i odredio asimptote razmatranog Dekartovog lista (slika 1)

 Veliki francuski matematičar Pjer Ferma (1601-1665), jedan od pionira u teoriji brojeva u kojoj je dao neke od najznačajnijih doprinosa, obogatio je matematiku sa dosta novih teorema. Sa jednim izuzetkom, sve su one do sada potvrđene uključujući i poznatu Formanovu poslednju teoremu. Izuzetak predstavlja Fermanova teorema o binarnim stepenima.

 U pismu Kenelenu Digbiju iz 1658., Ferma je pretpostaviio da brojevi oblika

Fn = 22n + 1,

koji se danas zovu Fermanovi brojevi, predstavljaju proste brojeve. Kako je F0 = 3, F1 = 5, F2 =17, F3= 257, F4= 65 537, pretpostavka je tačna za n = 0,1,2,3,4. medjutim Ojler he 1732. pokazao da za n = 5 Fermaova formula daje 

 F5 = 4 294 967 297 = 641 * 6 700 471,

Što znači da F5 nije prost broj. Inace, do sada nije pronađen nijedan novi Fermaov prost broj. Svi skorašnji rezultati ukazuju na pretpostavku da je Fn složen broj kad je n > 4.

 Kao poseban kuriozitet vezan za Fermaov broj F5, treba pomenuti slučaj Zire Kolberna (1804-1878), čoveka koji je posedovao neverovatnu sposobnost za brza aizračunavanja napamet. Posebno je bio uspešan z faktorizaciji velikih brojeva. Kada su ga pitali da li je Fermaov broj F5 = 4 294 967 297 (= 641 * 6 700 417) prost, oodgovorio je da nije jer ima delilac 641. jilbern nije bio u stanju da objasni način na koje je dobijao rezultate.

 Interesantno je napomenuti da je Maren Mersen u svom delu Novarum Observationum Physico-Mathematicarum (1647) takođe tvrdio da Fermaovi brojevi uvek daju proste brojeve.

 U svom čuvenom delu Disquisitiones arithmeticae ( Aritmetička istraživanja) iz 1801., čuveni nemački matematičar Karl Fridrih Gaus je pokazao da se pravilni n-tostrani poligon može konstruisati Euklidovim alatom (samo pomoću šestara i lenjira) ako i samo ako je broj n oblika

 n = 2mp1p2. . . pk,

gde je m nenegativni ceo broj a p1, . . . ., pk različiti Fermaovi prosti brojevi, ili je n = 2m (m > 1). Dakle, pravilni poligoni sa 3, 5, 17, 257 i 65 537 stranica (svi Fermaovi do sada poznati prosti brojevi) mogu se konstruisati pomoću šestara i lenjira. Ovo Gausovo otkriće povećalo je opšte interesovanje za Fermaove proste brojeve.

 Gaus je u 19. godini konstruisao pravilan poligon sa 17 stranica, koristeći rešenja binomne jednačine x 17 = 1. Bio je ta ko oduševljen ovim otkrićem da je odlučio da posveti život matematici. Postoje mnoge Euklidove konstrukcije pravilnog poligona od 17 (= F2) stranica. F.J.Rihelot iz Keningsberga je 1832. proučavao konstrukciju pravilnog poligona od 257 ( = F3) stranica.
Najkomplikovaniji slučaj, konstukcija poligona od 65 537 ( = F4) stranica, je zadivljujući ; Osvald Hermes iz Štiglica je potrošio deset godina svog života u konstruisanju takvog poligona. Njegov rukopis je izložen na matematičkom seminaru u Getingenu.

 Korišćenjem Gausove teorije kvadratnih ostataka može se pokazati da svaki prost faktor Fermaovih brojeva Fn ( n > 1) mora biti oblika 2n+2k+1, gde je k ceo broj. Na primer,

 F5 = (27 * 5 + 1) (27 * 52347 +1)
F6 = (27 * 1071 + 1) ( 28 * 262814145745 +1)
F7 = (29 * 116503103764643 +1) (29 * 11141971095088142685 +1)

 Ferma je otkrio (1640) a Ojler dokazao (1736) sledeće interesantno svojstvo, danas poznato pod nazivo Mala Fermaova teorema:

 Ako je p prost broj i a proizvoljan prirodan broj, tada je ap – a deljivo sa p.

Dokaz ove značajne teoreme je jednostavan:

Neka je p prost broj. Za a = 1 tvrđenje je tačno. Pretpostavimo da je p delilac broja ap – a i dokažimo da je p takođe delilac broja (a + 1 ). Koristeći binomnu formulu dobija se

  
Svaki od binomnih koeficijenata

Je deljiv sa p ako je p prost broj i ako je 1<= k <= p-1. Zaista, kako je p prost broj, p nije delilac broja k!. Dakle, broj p(p -1) . . . (p – k + 1) je deljiv sa k!, što znači da je (nk) deljivo sa p. Kako je prvi sabirak ap – a deljiv sa p, imajući na umu iduktivnu pretpostavku, sledi da je ( a + 1)p – ( a + 1) takođe deljivo sa p i dokaz Fermaove teoreme sledi na osnovu matematičke indukcije.

 Prema L. E. Dicksonu [ 39, Vol. I], izgleda da je slučaj kada je a = 2 bio poznat Kinezima još oko 500. godine P.N.E.; oni su, takođe, iskazali i obratno tvrđenje:

 Ako p deli 2p – 2, tada je p prost broj.

Ovo tvrđenje je ponovo otkrio i „dokazao” 1680. veliki nemački naučnik Gotgrid Lajbnic (1646-1716). Međutim, D. Mankle je utvrdio da ovo obratno tvrđenje nije tačno; ono pada, na primer, kada je p = 341 = 11 * 31, kao i ua beskonačno mnogo drugih vrednosti. Ukazujući na grešku, Manke je citirao Robertu Karmajklu (Carmichael, 1879-1967).

 U vezi deljivosti brojeva, pomenimo opet Lajbnica. Razmatrajući brojeve oblika nk – n, on je tvrdio da je za svaki prirodan broj n i za prve neparne brojeve k = 3, 5, 7, broj n³ - n deljiv sa 3, broj n5 –n deljiv sa 5 i n7 – n deljiv sa 7. rukovodeći se ovim specijalnim slučajevima Lajbnic je zaključio da je nk – n deljivo sa k za svaki neparan vroj k i proizvoljan priridni broj n. Međutim, vrlo brzo je otkrio da 2*9 – 2 = 510 nije deljivo sa 9. Lajbnic ja navodio ovaj primer kao ilustraciju pogrešnog zaključivanja posle nekoliko slučajeva koji zadovoljavaju „opštu formulu”, tako da se gornji primer ne može smatrati pogrešnom hipotezom. Ovaj primer je uključen samo kao kuriozitet koji se često pominje u literaturi.

 Nemački matematičar Kristijan Goldbah (1690 – 1760) naišao je na sličan problem 1742. U pismu Ojleru tvrdio je da je svaki broj oblika

gde su a i b celi brojevi, deljiv sa p ako i samo ako je p složen broj. Ojler (1707) je ukazao na grešku i dao sledeći kontraprimer: za a = 1, b= 1, p = 35 = 5*7 dobija se broj 2 na 35 -2 = 34 359 738 366, koji nije deljiv ni sa 5 ni sa 7.
Zapravo, tačno je sledeće tvrđenje:
Ako je p prost broj, tada je ( a + b) na p – a na p – b na p deljivo sa p.
Dokaz se može izvesti matematičkom indukcijom na sličan način kao kod Fermanove male teoreme.

 Poslednja teorema se može generalisati; naime, koristeći matematičku undukciju po n, može se pokazati sledeće tvrđenje:
Ako je n prirodan broj, a1,.......,an celi brojevi i p prost broj, tada je (Σak) na p – Σakp deljivo sa p.

 Čarls Bebidž (1791-1871), poznati matematičar i jedan od pionira u oblasti računarskih nauka, tvrdio je da je broj


deljiv sa n na 2 ako i samo ako ne n prost broj. Njegova pretpostavka bila je pogrešna. Evo kontraprimera: n = 16843 na 2 = 283686649 je najmanji složen broj koji se javlja kao delilac.

 Leonard Ojler (1707-1783) je 1732. tvrdio da je broj 2 na n – 1 ( Mersenovog tipa) prost broj za n = 41 i n = 47. C.B. de Vinšajm je primetio (1749) da je 2 na 47 – 1 deljiv sa 2351, dok je znatno kasnije G. Plana zapazio (1863) da je 13 367 činilac broja 2 na 41 – 1.

 Đovani Antonio Plana (1781-1864) je tvrdio u svom radu Mémoire sur la théorie des nombres (Mem. R. Acc. Sc. Torino (2) 20 (1863), 113-150, str. 141) da broj 2 na 53 – 1 nema činioce manje od 50 003. 45 godina kasnije A. Žerarden (Gérardin) je pronašao da ej 6361 delilac razmatranog broja.

 Rene Dekart je u svom pismu Mersenu od 15 novembra 1638. pisao da su svi prirodni brojevi oblika ps na 2, gde je p prost broj, savršeni. Dekart je dao sledeći primer:
p = 22021, s = 3*7*11*13 odakle je ps na 2 = 198 585 576 189,
ali je predvideo jednostavnu činjenicu da p nije prost broj; naime, p = 61*19 na 2, što je primetio istaknuti ekspert iz oblasti teorije brojeva L. E. Dickson (39, Vol. I, str. 12).

 Veliki matematičar Ojler, koji je pronašao kontraprimer u slučaju Fermaovih brojeva, napravio je takođe nekoliko grešaka tragajući za prostim brojevima uz pomoć eksplicitnih formula. Najpre, pretpostavio je (1772) da kvadratna forma n na 2 + n + 41 daje proste brojeve. Ovo je tačno za n = 0,1,2,......,39, ali sam Ojler je brzo pronašao da za n = 40 ovaj izraz ima vrednost 1681 = 41 na 2, što je, naravno, složen broj. H. M. Stark je dokazao 1967. da izraz n na 2 + n + M, gde je M > 41, ne predstavlja proste brojeve za M – 1 uzastopnu vrednost n.

 Druga Ojlerova „formula” za proste brojeve je bila 232 n na 2 + 1, takođe kvadratna forma, objavljena posle Ojlerove smrti u Comm. Arth. Coll II (1849). Iako ova formula generiše 76 prostih brojeva, A. Žerarden je našao (1908) dva izuzetka:

232*57 na 2 + 1 = 179*4211,
232*117 na 2 + 1 = 271*11719.
Osim ovih brojeva, postoji, naravno, beskonačno mnogo vrednosti za n za koje kvadratna forma 232 n na 2 + 1 daje složene brojeve.

 Zabeležimo da je Ojler dao još dve „formule” za proste brojeve:
p = 2 n na 2 + 29 generiše bar 29 prostih brojeva;
p = n na 2 – 79 n + 1001 daje 80 prostih brojeva.

 Neposredno pre svoje smrti Nikolo Tartalja ( 1500 – 1557) je zaključio da sume
1 + 2 + 4, 1 + 2 + 4 + 8, 1 + 2 + 4 + 8 + 16, 1 + 2 + 4 + 8 + 16 + 32, .....
neizmenično generišu proste i složene brojeve. Gornje sume su, ustvari, Mersenovi brojevi 2 na n – 1. Do kontraprimera se dolazi brzo; u Tartaljinom nizu 7 (prost broj), 15 (složen broj), 31 (prost broj), 63 (složen broj), 127 (prost broj), 255 (složen broj), sledeći član je 2 na 9 – 1 = 511 = 3 * 7 na 2, koji nije prost broj. Na grešku je ukazao L. E. Dickson (39, Vol. I, str. 9).

 Fransoa Eduar Lika (1842-1901) dao je u svojoj knjizi Théorie des Nombres, I (1891) netačnu faktorizaciju broja 2 na 58 + 1. Ovo je primetio V. P. Vorkman 1895. Inače, tvrđenje da su brojevi oblika 2 na n ± 1 prosti, bio je problem koji je privlačio pažnju mnogih matematičara dugi niz godina. Francuski matematičar T. F. De Lanji (Lagny, 1660-1734), koji je pronašao faktorizaciju pomenutog broja 2 na 58 + 1, dao je sledeći komentar u vezi sa tim problemom:
 „Faktorizacija broja 2 na 58 + 1 zahteva mnogo napora. Ovaj broj je deljiv sa 5 a rezultat je broj od 17 cifara koji ima dva devetovifrena prosta činioca. Ako bismo izgubili ove rezultate, morali bismo da radimo mnogo godina da bismo našli željenu faktorizaciju.”

Samo deset godina kasnije, Orifej (Aurifeuille) je primetio da je

Ovaj rezultat se može lako uopštiti:

 Šarl de Buvel (Charles de Bouvelles, 1470-1553) je tvrdio u svom radu Liber de Perfectis Numeris (Paris, 1509) da su svi brojevi dobijeni Euklidovom formulom:

Za n ≤ 39 savršeni. Gornja Euklidova formula generiše savršene brojeve (sve parne) ako i samo ako je 2 an n – 1 prost broj, što je dokazao Ojler nekih 2000 godina posle Euklidovog tvrđenja.

 Engleski matematičar Robert Rikord (1510-1558) napisao je 1557. da su brojevi 130 816, 2 096 128 i 536 854 528 savršeni, što je pogrešno. Ova greška je otkrivena tek 1919., kada je na nju ukazao L. E. Dickson (39, Vol. I, str. 9).

 Jedan problem, postavljen u devetnaestom veku, sastojao se u nalaženju dva pozitivna racionalna broja čiji je zbir kubova jednak 6. Veliki francuski majtematičar Adrien Mari Ležandr dao je „dokaz nemogućnosti” takve reprezentacije. Međutim, nekoliko decenija kasnije, veliki britanski sastavljač matematičkih zagonetki Henri Djudeni (Henry Dudeney, 1857-1930) oborio je njegov dokaz i dao vrlo jednostavno rešenje:
6=
Primetićemo da je ovaj problem bio „dečja igra ” za Djudenija u poređenju sa sličnom reprezentacijom dva pozitivna racionalna broja (ne cela) čija suma kubova iznosi 9. On je pronašao da razlomci

  i 

zadovoljava željeni uslov. Njegovo rešenje zaslužuje iskreno divljenje ako se uzme u obzir da nije posedovao nikakvu računsku mašinu.

 Fermaova poslednja teorema iz 1670. tvrdi da ne postoje celobrojne vrednosti x, y, z koje zadovoljavaju diofantovu jednačinu x na n + y na n = z na n ( xyz ≠ 0) ako je n≥ 3. Ojler je razmatrao opštiji slučaj, koji bi, ukoliko bi bio tačan, uključivao Fermaovu poslednju teoremu kao specijalni slučaj. Naime, Ojler je verovao da nijedan n-ti stepen veći od 2 ne može biti suma manje od n n-tih stepena prirodnih brojeva.
Ovo je tačno za n = 3, jer se ovaj specijalni slučaj svodi na Fermaovu poslednju teoremu. Medjutim, 1966., dva veka nakon što je Ojler postavio ovu hipotezu, Leon L. Lander i Tomas R. Parker su pronašli kontraprimer uz pomoć računara. Ovaj kontraprimer je pronađen za n = 5 i glasi

Kao što se može videti, peti stepen je izražen kao zbir samo četiri petih stepena. Primetimo da su bila potrebna dva veka i pomoć računara da bi se otkrilo da Ojler nije bio u pravu. Noam Elkiz (Elkies) sa Univerziteta u Harvardu dao je 1988. kontraprimer za četvrte stepene:

 Galileo Galilej (1564-1642) nije rešio problem najbržeg pada, mada je znao za cikloidu. U stvari, on je bio jedan od prvih koje je skrenuo pažnju na ovu krivu i preporucio korižćenje cikoide za svodove u arhitekturi. Galileo je 1599. pokušao da izračuna površinu ograničenu lukom ciklode i apcisnom osom. U ovom pokušaju on je koristio metod upore đivanja ciloidalnog šablona određenjog veličinom generišućeg kruga. Nepravilno je zaključio da je tražena površina veoma blizu ( ali ne i jednaka) 3r2p (trostrukoj površini kruga), gde je r poluprečnik generišućeg kruga.

Prvo tačno izračunavanje površine između luka cikloide i apscisne ose izveli su nazavisno Francuz Žil Person de Roberval (Gilles Persone de Roberval, 1602-1675) oko 1637. i Galilejev učenik Evangelista Toričeli (Torricelli, 1608-1647) oko 1644. Obojica su našli da je površina jednaka tačno trostrukoj površini generišuceg kruga, to jest, 3r2p. Toričeli je koristio metod koji podseća na infinitezimalni račun (pra-infinitezimalni račun). Zapazimo da je danas ovaj problem jednostavna vežba u okviru standardnog kursa o integralnom računu.

 Ovo je kratka priča o latinskim i Ojlerovim kvadratima i jednoj pogrešnoj hipotezi velikog matematičara Leonarda Ojlera. Latinski kvadrat reda n sastoji se od n različitih simbola, uređenih u obliku kvadratne šeme na takav način da se svaki simbol javlja samo jednom u svakoj vrsti i samo jednom u svakoj koloni. Drugim rečima, svaka vrsta i svaka kolona je jedna permutacija od n simbola. U svom članku Recherches sur une nouvelle espaċe de quarres magiques (Istraživanja o novoj vrsti magičnih kvadrata), Ojler je pisao o ovoj vrsti magičnih kvadrata. Danas se ovi kvadrati zovu latinski kvadrati, jer je Ojler koristio obična latinična slova kao simbole koje treba rasporediti. 

 (slika 6) 

 Slika 6a pokazuje latinski kvadrat četvrtog reda sačinjen od latinskih slova a, b, c i d koja su uređena na opisani način. Slika 6 takođe predstavlja jedan latinski kvadrat sa četiri odgovarajuća grčka slova. Superpozicija ovih kvadrata, prikazana na slici 6c, daje kvadratnu šemu parova u kojima je svako latinično slovo kombinovano jednom i samo jednom sa grčkim slovom. Kvadrat dobijen takvom kombinacijom zove se Ojlerov kvadrat ili grčko-latinski kvadrat. Za dva kombinovana kvadrata se kaže da su ortogonalni kvadrati. Primetimo da se grčko-latinski kvadrati često koriste za dizajniranje eksperimenata u biologiji, medicini, sociologiji i marketingu.

 U Ojlerovo vreme billi su poznati grčko-latinski kvadrati reda3, 4 i 5. Ojler se pitao šta je sa kvadratom reda 6? Godinu dana pre nego što je umro (1782) Ojler je razmatrao ovo pitanje u okviru sledećeg problema:

Da li je moguće rasporediti 36 oficira od kojih svaki ima jedan od 6 različitih činova i pripada jednom od 6 različitih pukova, u kvadaratnu formaciju 6 x 6 tako da svaka vrsta i kolona sadrži tačno jednog oficira svakog ranga iz svakog puka? Ovaj čuveni problem poznat je kao Ojlerov problem oficira.

 Ojler je pokazao da problem n na2 oficira, koji je ekvivalentan konstrukciji grčko-latinskog kvadrata reda n, može uvek da se reši ako je n neparno ili deljivo sa 4. Nadalje je tvrdio da grčko-latinski kvadrati reda 6, 10 i 14, i uopšte svi kvadrati reda n = 4k + 2 ne mogu biti konstruisani. Ova pretpostavka je postala poznata pod nazivom Ojlerova hipoteza.

 Ojlerovo tvrđenje za specijalni slučaj kada je n = 6 dokazao je francuski matematičar Gaston Tari 1901. godinef, dakle 118 godina kasnije. Nakon Tarija nekoliko matematičara je čak objavilo dokaze da je hipoteza tačna, ali je u svim tim „dokazima” kasnije bila pronađena greška.

 Tarijev rad je bio veoma naporan i težak jer su on i njegovi saradnici primenili iscrpljujući metod olovke-i-papira. Iz tog razloga je sledeći specijalni slučaj za n = 10 morao da čeka kompjutersko doba. Ojlerova pretpostavka je opovrgnuta 1959., dakle 177 godina kasnije, kada su R. C. Bouz ( Bose) i S. S. Šrikand (Shrikhande) (sa Univerziteta Južna Karolina) pronašli grčko-latinski kvadrat reda 22 korišćenjem modifikovanog Kirkmanovog sistema, a zatim je E. T. Parker pronašao kvadrat reda 10. Parker je primenio genijalan pristup koji se bazira na korišćenju jednog ulaza u svakoj vrsti i koloni, tako da nijedna dva ulaza ne sadrže istu cifru. Ukupno vreme potrebno za izvršenje ovog programa na sporom računaru iz 1959. bilo je manje od jednog minuta.

Metodi istraživača su postali sve rafiniraniji; nedvosmisleno je utvrđeno da je Ojlerova hipoteza netačna za sve vrednosti n = 4k + 2, kada je n veće od 6.

 Parkerov grčko-latinski kvadrat 10. reda

Vest da je Ojlerova hipoteza opovrgnuta objavljena je na naslovnim stranama svetske štampe. New York Times od 26. aprila 1959. je objavio opširan članak. Parkerov grčko-latinski kvadrat reda 10, prikazan na slici 7, ima za simbole cifre od 0 do 9; cifre sa leve strane svakog polja pripadaju prvom latinskom kvadratu, dok cifre sa desne strane pripadaju drugom latinskom kvadratu.

 Džon Hil (John Hill) je napisao u svojoj knjizi Arithmetic both in Theory and Practice (1727) da je broj 11826 jedini broj čiji kvadrat (=139854276) daje devetocifreni broj napisan svim ciframa od 1 do 9. Leonard Dikson, profesor sa Čikaškog univerziteta, opovrgao je Hilov rezultat 1920. On je pronašao druge brojeve koji takođe poseduju ovu osobinu. Jednostavan kompjuterski program daje petocifrene brojeve A sa željenom osobinom.

 Dzon Valis (1616-1703), jedan od najuglednijih ljudi Njutnovih savremenika, bio je prvi matematičar koji je pokušao da pronikne u suštinu imaginarnih brojeva i njihovu geometrijsku reprezentaciju.
Njegova osnovna ideja mogla bi se objasniti pomoću slike 8.
Jedinični krug sa centrom u O  seče x-osu dajući odsečak +1 u tački A i odsečak u tački B. Njegov presek sa y-osom daje tačku C koja predstavlja imaginaran broj.

 Medjtim, poznato je iz geometrije da normala OC povučena na prečnik iz tačke koja ležI na kružnici predstavlja geometrijsku sredinu odsečaka OB i OA, dakle, OC =.

Odatle je OC==. Zaista, tačka C predstavlja imaginarnu jedinicu i=,
ali Valisovo rezonovanje ima jednu grešku. Naime, on razmatra OC kao geometrijsku sredinu odsečaka koji leže na prečniku, pri čemu je jedan pozitivan, a drugi negativan.
Medjutim, terema o normali i segmentima jasno pretpostavlja da su segmenti pozitivni.

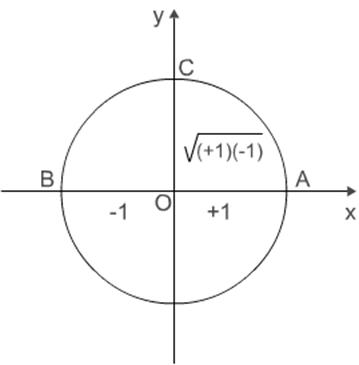
Sl. 8. Valisova reprezentacija imaginarne jedinice

LITERATURA

• MIODRAG PETKOVIĆ i LJILJANA PETKOVIĆ, Matematički vremeplov
• INTERNET, WIKIPEDIA-ENCIKLOPEDIJA

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi