KONUSNI PRESECI

Konusni preseci zauzimaju kako u geometriji tako i u celoj matematici veoma značajno mesto. Smatra se da ih je otkrio grk MENEHMO (IV vek stare ere) i to kao presek konusa sa ravnima koje su normalne na izvodnice konusa. Vrsta preseka zavisi od ugla kod vrha konusa, tj. presek je elipsa, parabola ili hiperbola, zavisno od toga da li je ugao  oštar, prav ili tup.
Apolonije iz Perge(oko 262 - oko 180.pre.n.e), grčki matematičar i astronom, izložio je opširnu i veoma detaljnu teoriju konusnih preseka u osam knjiga, čije su četiri prve sačuvane na grčkom jeziku a tri sledeće u arapskom prevodu a osma knjiga je izgubljena. Po njemu, konusni preseci su ravni preseci jednog pravog ili kosog konusa sa kružnom osnovom. Dao je i danas aktuelne nazive elipsa, parabola i hiperbola. Najznačajnija su njegova proučavanja normala na konusne preseke ( peta knjiga).
I drugi matematičari raznih epoha bavili su se teorijom konusnih preseka i pisali mnoge rasprave o tom pitanju. Značajno je delo francuskog matematičara i filozofa Paskala ( XVII vek ), a jednu od najsavršenijih ne analitičkih teorija konusnih preseka izradio je naš matematicar Rudjer Bošković ( XVIII vek ).
Uvodjenjem analitičke geometrije teorija konusnih preseka znatno se uprošćuje. Zaista, analitičkim metodama jednostavno se dokazuju mnoge osobine tih krivih linija, čiji su dokazi sintetičkim ( tj. ne analitičkim ) metodama bili često veoma složeni.
Medjutim, koliko je analitička geometrija doprinela kompletiranju teorije konusnih preseka, toliko su konusni preseci doprineli razvoju analitičke geometrije. Pored toga, njihov značaj je ogroman i u raznovrsnim primenama: optici, mehanici, astronomiji, tehnici i drugim oblastima. U optici se njihov značaj naročito sastoji u konstrukcijama ogledala i sočiva. Priča se da je još Arhimed ( koji je dobro poznavao osobine konusnih preseka, a naročito parabole ) konstruisao parabolička ogledala pomoću kojih je koncentrisao sunčeve zrake i zapalio rimske brodove, koji su napadali njegov grad Sirakuzu.
Ipak, najveći značaj konusni preseci su dobili kada je Njutn dokazao Keplerove zakone o kretanju planeta oko sunca. Putanje planeta i njihovih satelita su elipse, a putanje kometa su parabole ili hiperbole.

Osobine konusnih preseka

 Neka su u prostoru zadate prave p i s  koje se seku u tački O. Skup svih slika tačaka prave p u rotacijama sa osom s je prav kružni konus. Tačku O zovemo temenom konusa, pravu s osom, a slike prave p u rotacijama oko prave s njegovim izvodnicama.
Presek proizvoljne ravni Ω i tog konusa zovemo konusnim presekom. Ako je ravan Ω upravna na s, a ne sadrži O, konusni presek je krug. Postoji sfera koja dodiruje konus u tačkama tog kruga. Za takvu sferu ćemo reći da je upisana u konus. Ako ravan Ω sadrži O njen presek sa konusom može da bude ili samo tačka O , ili skup tačaka jedne izvodnice, ili skup tačaka koje pripadaju dvema izvodnicama tog konusa.
Ako ravan ne sadrži tačku O i nije upravna na  s , konusni presek ćemo zvati konikom. Ostale konusne preseke ćemo zvati i degenerisanim konikama.

Sledeća teorema karakteriše konike:

Teorema. Svaki konusni presek , osim kruga, jeste geometrijsko mesto tačaka u ravni za koje je odnos rastojanja od neke stalne tačke F (žiže) i neke stalne prave DD’ (direktrisa)  stalna veličina.

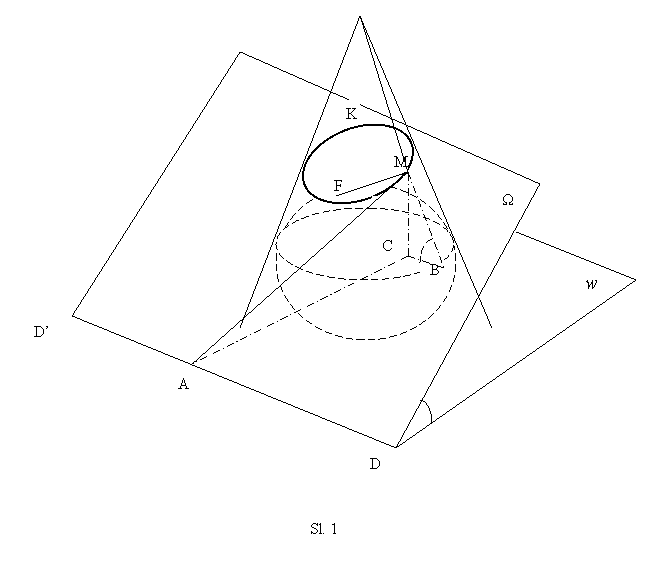
Dokaz: Obeležimo sa K konusni presek dobijen sečenjem konusa sa ravni Ω i upišimo u taj kružni konus loptu koja dodiruje ravan Ω u tački F. Lopta dodiruje konus po krugu koji leži u ravni w . Ravni Ω i w se seku duž prave DD’. Uzmimo proizvoljnu tačku M krive K i iz nje spustimo normalu MA na pravu DD’. Konstruišimo izvodnicu MB konusa, gde je tačka B prodor te izvodnice kroz ravan w. Ugao između ravni Ωi w označimo sa a, a sa b ugao između izvodnice konusa i ravni w, i sa k=MC odstojanje tačke M od ravni w. (sl. 1)
Važi sledeće:

 MB=k / sinb, AM=k / sina

 i MB=MF (kao dužine tangenata na loptu povučene iz tačkeM).

Formirajmo sada odnos rastojanja MF(=m), tačke M od tačke F, i rastojanja AM(=d), tačke M od prave DD’. Na osnovu ovih veza vidimo da je odnos

MF/ AM= MB/ AM = sina / sinb = e = const., ili m / d=e
stalan za ma koju tačku konusnog preseka

Stalnu tačku F zovemo fokus ili žiža, stalnu pravu DD’ direktrisa ili vodilja, i stalnu vrednost e, odnos rastojanja ma koje tačke konusnog preseka od fokusa i direktrise zovemo ekscentricitet konusnog preseka.

Konusni presek se zove elipsa ako je e< 1, hiperbola ako je e > 1, I parabola ako je e = 1.

U slučaju elipse i parabole sve tačke ovih linija nalaze se samo sa jedne strane i to sa one strane direktrise gde se nalazi i žiža.
U slučaju hiperbole tačke ove linije se nalaze sa obe strane direktrise. Hiperbola ima dve grane koje su sa različitih strana direktrise.

Polarna jednačina konusnih preseka

Uzmimo žižu F za pol polarnog koordinatnog sistema, a polarna osa neka je normalna na direktrisu DD’. Sa p označimo rastojanje od žiže F tačke M1 konusnog preseka koja se nalazi na pravoj normalnoj na polarnoj osi i prolazi kroz žižu. Veličina p se zove parametar konusnog preseka. Pošto tačka M1 pripada konusnom preseku važi:

 M1F/ M1M2= p/ FB= e, ili FB=p/ e

a ako sa M označimo ma koju tačku konusnog preseka, važi:

 MA = FB - MF cosq = p/ e - m cosq.

A na osnovu definicije konusnog preseka važi:

m/ d= MF/ MA= e, MA= d ili
m/ (p/e - m cosq )= e.

I upravo rešavajući ovu poslednju jednačinu po veličini m dobijamo polarnu jednačinu konusnih preseka :

m = p/ (1 + e cosq ).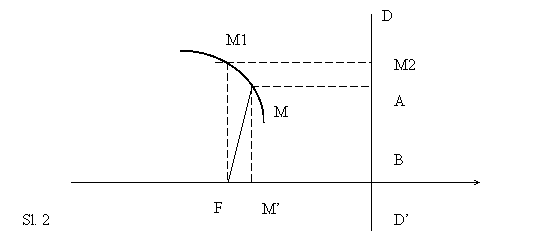 

Pošto se polarna jednačina konike ne menja ako q zamenimo sa -q, konika je osno simetrična u odnosu na polarnu osu x. Kada je q =0, onda je m = p/ (1 +e), a kada jeq = π , onda je m = p/ (1 - e), pa konika seče x osu u dvema tačkama, osim ako je e=1.
Ako je e < 1 iz polarne jednačine konike sledi da je za sve vrednosti q , m konačno i pozitivno pa je stoga, elipsa zatvorena kriva. Ako je e =1, mje i dalje konačno i pozitivno za sve vrednosti q osim za q = π . Parabola nije zatvorena jer je vrednost m ne definisana za q = π. Ako je e >1, mje pozitivno ili negativno u zavisnosti od toga da li je  cosq veći ili manji od -1/e. Zato se hiperbola sastoji iz dveju odvojenih grana zadatih sa
-a< q< a , -a< q< 2π -a,
gde je a= arccos(-1/e).

Kretanje planeta. U astronomiji je poznato da je putanja planete u polarnom koordinatnom sistemu, m=f(q), određena diferencijalnom jednačinom
f -1 + d2 (f -1)/ dq2  = const.

Rešavanjem jednačine dobija se f -1 = a cosq+ b sinq + γ, odnosno promenom polarne ose,

f(q)= 1/ ( a cosq + γ).

Putanje planeta, kometa i asteroida su u prvoj aproksimaciji konike u čijem se jednom fokusu nalazi sunce.

Jednačina konusnih preseka u Dekartovim pravouglim koordinatama

Polarnu jednačinu konike napišimo u sledećem obliku:

 p = m (1 + e cos q) , m2= (p – e m cosq )2

Polazeći od poznatih obrazaca

 x = m cos q , y = m sin q

imamo sledeću jednačinu konusnog preseka u Dekartovim pravouglim koordinatama

 (1 - e2) x2 + y2  + 2 epx - p2 = 0 . ( 1)
Pretpostavimo da je 1 - e2 ≠ 0, tj. da konusni presek predstavlja elipsu ili hiperbolu . Izvršimo translaciju koordinatnog sistema u tački O’(x1, x2)

 x= x’+x1, y=y’+y1 .
Formule translacije treba uzeti u sledećem obliku:

 x’ = x + e p/( 1 - e2 ) i y’ = y .
 
gde su sa x’ i y’ označene nove koordinate.
 
 (1 - e2) x’2 + y’2 - p2 / (1 - e2) = 0.
 
Ako uvedemo i nove veličine a  i b, a2 = p2 / (1 - e2) 2 , b2 = p2/ (1 - e2)
onda dobijamo:

za elipsu (e < 1): x’2/ a2  + y’2  / b2 = 1;  (2)

za hiperbolu (e > 1): x’2/ a2 - y’2  / b2 = 1;  (3)

Jednačine (2) i (3) se zovu kanonske jednačine elipse i hiperbole .
 Veličine a i b  nazivamo poluosama elipse , odnosno poluosama hiperbole.Parametar  p i ekscentritet e se mogu izraziti i preko poluosa,

za elipsu : p= b2 /a, e=( a2 - b2) 1/2 / a <1,
za hiperbolu:  p= b2 /a, , e=( a2 + b2) 1/2 / a >1.

U slučaju parabole važi e = 1 jednačina u Dekartovim koordinatama  je:

 y2 + 2 p x - p2 = 0
 y2 - 2p( -x+ p/2)=0.

Uvodimo nove koordinate x’ i y’ : x’ = -x+ p/2  i y’ = y

Nova jednačina parabole posle smene je : y’2 = 2 p x’ .  (4)

Ova jednačina (4) se zove temena jednačina parabole.

Fokusne osobine elipse i hiperbole

Da bismo utvrdili fokusnu osobinu elipse koristićemo polarni koordinatni sistem sa polom u fokusu F i polarnom osom Fxnormalnom na direktrisi DD’. Na produžetku polarne ose uzmimo tačku F1 na rastojanju c1 od fokusa F i izračunajmo rastojanje proizvoljne tačke M elipse
m= p/ (1 + e cosq ) 
od te tačke F1:
 | MF1|2= m 2 + c12  + 2m c1 cosq.
Možemo eliminisati veličinu qpomoću jednačine elipse, pa pomenuto rastojanje izraziti na sledeći način:
 | MF1|2 = m 2 - 2c1m / e +2 pc1/ e +c12 . 

Da bi ovaj izraz na desnoj strani bio tačan kvadrat | MF1|2 = (m- c1/e) 2 ,  mora c1 zadovoljavati sledeći uslov

 2 pc1/ e +c1 2 = c12/ e2,  ili c1=2ep/ (1- e2 ). (5)

Važe sledeće relacije:

 m ≤ p/ (1- e)  i 2/ (1+ e)>1.

 Zato sada iz relacije (5) redom sledi:

c1/e= 2p/ (1- e2) = 2/ (1+ e) * p/ (1- e) > p/ (1- e) ≥ m ili

m - c1/e= m - 2p/ (1- e2) ≤ 0.

Vrednost traženog rastojanja je:

|MF1|= c1/e - m= 2p/ (1- e2) - m .

Ako stavimo m= |MF|, onda za svaku tačku elipse postoji sledeća relacija

|MF| + |MF1|= 2p/ (1- e2)= const.

Zbir odstojanja proizvoljne tačke M elipse od dve stalne tačke F i F1 je konstantan.
Ova fokusna osobina često se koristi radi definisanja elipse kao linije u ravni. Tačke F i F1 zovu se fokusi ili žiže elipse . Ako stavimo 2c=c1 i uzmemo u obzir prethodna razmatranja, videćemo da se c, polovina odstojanja između fokusa, na sledeći način ižražava pomoću poluosa:

c=(a2 - b2) 1/2 .

Ekscentricitet možemo sada definisati na sledeći način:
 e= c/ a.
Analogno i za hiperbolu može da se utvrdi da važi sledeće: razlika rastojanja proizvoljne tačke M hiperbole od dve stalne tačke je konstantan.

 Temene jednačine konusnih preseka

Ako u jednačini (1- e2 )x2 + y2  + 2 epx - p2 = 0 izvršimo transformaciju koordinata pomoću formula translacije:

 x = x1- (p+ ep)/ (1- e2), y=y1,

onda ćemo odmah dobiti tzv. temene jednačine konusnih preseka (sl. 3)

 y1 2 = 2px1+ (e2- 1) x12. (6)

Za slučaj e =1 dobija se ranije poznati oblik temene jednačine parabole.

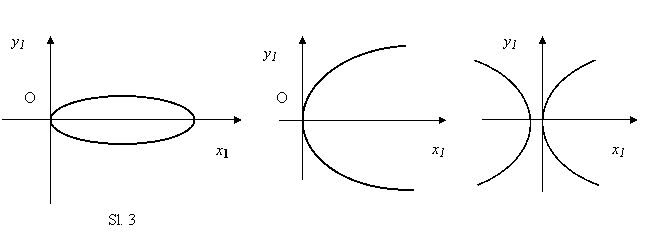
Lako je sada dati geometrijsko tumačenje jednačine (6).
U slučaju elipse je y12< 2px1,

u slučaju hiperbole  y12 > 2px1  i

u slučaju parabole  y12 = 2px1.

Prema tome za proizvoljnu tačku krive površina kvadrata sa stranicom y1 je manja, veća, jednaka površini pravougaonika sa osnovicom x1 i visinom 2p- ’’fokusni presek ’’ krive. (sl. 4)
Ovo svojstvo je doprinelo da se konusni preseci zovu elipsa, hiperbola i parabola.
Reč elipsa od grčke reči ελλειψιζ (nedostatak) – kazuje nam da površini kvadrata y12  nedostaje površina veličine (e2- 1) x12 pa da bude ista sa pravougaonikom 2px1.

Reč hiperbola od grčke reči νπερβολη (suvišak) – kazuje nam da kvadrat ima veću površinu prema površini pravougaonika za (e2- 1) x12.

Reč parabola od grčke reči παραβολη(jednakost) – kazuje nam da su nam u ovom slučaju površine pravougaonika i kvadrata jednake.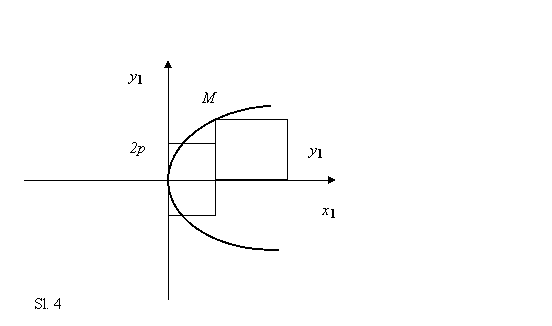

Opšta algebarska jednačina II stepena

 Opšta algebarska jednačina drugog stepena

2f(x, y) ≡ a11 x2 + 2a12 xy + a22 y2 + 2a13 x +2a23 y + a33 = 0 (7)

može se svesti na jedan od kanonskih oblika jednačina konusnih preseka, na temenu jednačinu parabole, kao i na jednačine para pravih linija. Da bismo to pokazali izvršićemo obrtanje ose koordinatnog sistema za ugao φ pa će dati koordinatni sistem Oxy , u odnosu na koji posmatramo jednačinu (7), postati nov sistem Ox’y’. Postoje sledeće veze između starih i novih koordinata:

 x = x’ cos φ – y’ sin φ,
 y = x’ sin φ + y’ cos φ .

Jednačina (7) u novim koordinatama x’ i y’ postaje:

A11 x’2 + 2A12 x’y’ + A22 y’2 + 2A13 x’ +2A23 y’ + A33 = 0 , (7’)

gde su novi koeficijenti Aikodgovarajuće funkcije starih koeficijenata i ugla  φ rotacije. Mi ćemo ugao rotacije izabrati tako da koeficijent A12bude jednak nuli, tj. tako da ni jednačina (7’) ne sadrži član sa proizvodom x’y’. Takav ugao φ se određuje na osnovu uslova

 (a11 -a22 ) sin2φ = 2 a12 cos2 φ, (8)

 ili  tg 2φ =2 a12 / (a11 -a22  ).

Ugao φ je uvek moguće odrediti pri uslovu a11 ≠ a22  na osnovu (8) tj. uvek je moguće odrediti takav koordinatni sistem Ox’y’ da bi jednačina (7’) bila bez člana proizvoda x’y’:

A11 x’2 + A22 y’2 + 2A13 x’ +2A23 y’ + A33 =0. (9)

Posmatrajući jednačinu (9) razlukovaćemo sledeća dva slučaja:
a) A11 A22 ≠ 0,
b) jedan od koeficijenata A11 ili  A22 je jednak nuli. Uzmimo da je A22= 0

U slučaju pod a) moguće je definisati translaciju koordinata pomoću formula
x’= x1 - A13 / A11,  y’= y1 – A23 / A22
na osnovu kojih jednačina (9) dobija sledeći oblik

 A11 x12 + A22 y12 + B= 0 , (10)

gde je novi slobodni član B određena funkcija starih koeficijenata. U vezi sa jednačinom (10) razlikovaćemo pet mogućih slučajeva:

a1) B ≠ 0 i znaci koeficijenata A11 i A22  su isti, tj. A11 A22 >0, ali su suprotni znaku koeficijenta B. Jednačina (10) predstavlja elipsu, jer se može svesti na oblik
 x12 / a2 + y12 / b2= 1

kada se uvedu sledeće oznake
A11 a2 = A22 b2= -B.

a2) B ≠ 0  i znaci koeficijenata A11 i A22  su suprotni, tj. A11 A22 < 0. Moguće je uvesti nove veličine pomoću veza a i b pomoću veza
-A11 a2 = A22 b2= B.
i jednačinu (10) svesti na poznati kanonski oblik jednačine hiperbole

x12 / a2 - y12 / b2= 1.

a3) B ≠ 0  i znaci koeficijenata A11 i A22  su jednaki znaku koeficijenta B. Jednačina (10) predstavlja imaginarnu krivu ( ’’imaginarna elipsa’’ )

x12 / a2 + y12 / b2+ 1=0,
jer se sada nove veličine a i b mogu uvesti sledećim vezama
A11 a2 = A22 b2= B.

a4) B=0  i znaci koeficijenata A11 i A22  su  različiti, tj. A11 A22 < 0. Sada je moguće levu stranu jednačine (10) napisati u obliku proizvoda dva realna faktora
 [x1 –( - A22 / A11) 1/2 y1 ] * [x1 +( - A22 / A11) 1/2 y1 ]=0.
Jednačina (10), dakle predstavlja par pravih linija;

a5) B=0  i znaci koeficijenata A11 i A22  su  jednaki, tj. A11 A22 > 0. Jednačinu (10) je moguće svesti na sledeći oblik

 [x1 –i( - A22 / A11) 1/2 y1 ] * [x1 +i(A22 / A11) 1/2 y1 ]=0. ( -1) 1/2 ≡ i
i ona predstavlja ’’ par imaginarnih pravih’’ koje se seku u realnoj tački
(0, 0).

 b) U ovom slučaju se može koristiti sledeća translacija
x’= x1 - A13 / A11,  y’= y1

pomoću koje jednačina (9) dobija sledeći oblik

 A11 x12 + 2 A23 y1 + D= 0 , (11)

gde se novi slobodni član D izražava pomoću starih koeficijenata. U vezi sa jednačinom (11) imamo četiri sledeće varijante:

b1)   A23 ≠ 0. Moguće je definisati translaciju

 x1 = x’’, y1 = y’’- D/ 2 A23

i jednačinu (11) svesti na poznati oblik jednačine parabole:

 A11 x’’2 + 2 A23 y’’ = 0 , ili x’’2  = 2 p y’’.

b2)   A23 = 0  i koeficijnti  A11  i D su suprotnog znaka. Jednačina (11) u ovom slučaju predstavlja par realnih paralelnih pravih

 x1 = ± ( - D/ A11 ) 1/2.

b3) A23 = 0  i koeficijnti A11  i D su istog znaka. Tada imamo:

 x1 = ± i( + D/ A11 ) 1/2,

a to predstavlja par ’’paralelnih imaginarnih pravih’’.

b4) A23 = 0 i  D = 0. U ovom slučaju imamo par pravih
x12 = 0.
koje se poklapaju.

Prema tome, opšta algebarska jednačina drugog stepena predstavlja: ili konusni presek, ili par pravih, ili tačku ( imaginarne prave koje se seku u realnoj tački) , ili imaginarnu elipsu, ili paralelne imaginarne prave.

 Elementi konusnih preseka

Elementom konusnog preseka naziva se svaka tačka, svaka prava, svaki skup tačaka, svaki skup pravih koje se određuju pomoću jedne ili više relacija koje sadrže koeficijente iz jednačine datog konusnog preseka.
Poći ćemo od opšte jednačine:

2f(x, y) ≡ a11 x2 + 2a12 xy + a22 y2 + 2a13 x +2a23 y + a33 = 0 (12)

1) Prečnik.Prečnik ili dijametar je geometrijsko mesto sredina paralelnih tetiva konusnog preseka.

Neka je ma koja tetiva krive (12) određena jediničnim vektorom  s {m,n}, čije su koordinate kosinusi uglova α i β  koje on zaklapa sa osama pravouglog Dekartovog koordinatnog sistema Oxy. Premestimo početak sistema Oxy   u neku novu tačku O1 ( a,b) i primenimo poznate obrazce za translaciju:
 x= a+ x1, y=b+ y1.
Transformisana jednačina u odnosu na novi sistem O x1 y1 ima sledeći oblik:
a11 x12 + 2a12 x1y1 + a22 y12 + 2( fa’ x1 +fb’ y1) +2f ( a,b )= 0, (13)

gde smo upotrebili sledeće oznake:

 fa’ ≡ fx1’ ( a,b), fb’ ≡ fy1’ ( a,b),
 fx1’ ( x1 , y1 ) ≡ a11 x1+ a12 y1 + a13,
 fy1’ ( x1 , y1 ) ≡ a21 x1+ a22 y1 + a23 , ai k = ak i , ( i,k = 1,2).

U novom koordinatnom sistemu tetiva koja prolazi kroz početak i paralelna je vektoru s , ima ove parametarske jednačine ( t je parametar) :

x1 = mt, y1 = nt. (14)

Eliminacijom x1 i y1  iz jednačina (13 ) i (14) dobijamo uslov :

(a11 m2 + 2a12 mn + a22 n2 ) t2 + 2( fa’ m+fb’ n) t+2f ( a,b )= 0

za određivanje onih vrednosti parametra t koje odgovaraju tačkama preseka prave (14) i krive (13). Ako tačka ( a,b ) treba da leži na sredini tetive, onda mora da važi:
 fa’ m + fb’ n = 0 .
Mi tražimo geometrijsko mesto sredina svih tetiva , tj. one tačke ( a,b ) koje zadovoljavaju poslednji uslov. Zato zamenom veličina a i b sa tekućim koordinatama x i y dobijamo:
 fx’ m +fy’ n = 0

jednačinu dijametra.
Stavimo m = cosα, n =sinα i n/ m = tgα = k, i tada jednačinu dijametra, prave linije, možemo pisati u jednom od sledećih oblika
 fx’ + kfy’ = 0 (15) ili

 ( a11 x + a12 y + a13 ) + k (a21 x + a22 y + a23 )= 0, (16)

gde je k ugaoni koeficijent paralelnih tetiva. Za prečnik ili dijametar (15), ili (16) kažemo da je spregnut  ili konjugovan sa pravcem k.Koeficijent pravca k1dijametra  (16) je:
k1 = - ( a11 + a12 k ): (a12 + a22 k ).

Poslednja relacija se može napisati u simetričnom obliku u odnosu na veličine k i k1:
a22 k k1 + a12 (  k + k1 ) + a11 = 0. (17)

Za prečnik koji je konjugovan sa pravcem k1 kažemo da je konjugovan sa prečnikom (16) i prema tome ugaoni koeficijenti dva uzajamno konjugovana prečnika zadovoljavaju vezu (17).

2) Ose. Dvauzajamno normalnaprečnika zovu se ose konusnog preseka. Ugaoni koeficijent u osa odredićemo na sledeći način. Zbog uslova ortogonalnosti pravca k i k1
k k1 + 1= 0

uslov (17) se može napisati u obliku
 k + k1 = - ( a11 - a22 ): a12 .

Na osnovu ovih uslova vidimo da su k i k1 koreni sledeće kvadratne jednačine:
a11 u2 +( a11 - a22 ) u - a12 = 0.

3) Centar. Preseci uzajamno konjugovanih prečnika daju centar konusnog preseka. Koordinate centra dobijamo rešavanjem linearnih jednačina kojima su određeni konjugovani prečnici. Posmatraćemo jednačinu (13). Ako izaberemo koordinate ( a, b) novog početka tako da pomenuta jednačina bude bez linearnih članova tj. da ima sledeći oblik:

 a11 x12 + 2a12 x1y1 + a22 y12 +2f ( a,b )= 0,

onda moraju postojati uslovi
 fa’ = 0,  fb’ = 0

ili napisati u razvijenom obliku
a11 a+ a12 b + a13 = 0,
 a21 a+ a22 b + a23   = 0.

Ovako izabrani koordinatni početak, čije koordinate zadovoljavaju ove uslove jeste centar krive, i upravo ove jednačine služe za određivanje koordinata centra konusnog preseka.
Da bi ovaj linearni sistem imao rešenja po veličinama a i b, tj. da bi kriva drugog reda imala centar, mora determinanta sistema da bude različita od nule
 I1 ≡ a11 a22 - a12 2 ≠ 0.

Krive drugog reda sa centrom su elipsa I hiperbola, a bez centra je parabola ( I1= 0).

4) Temena. Preseci konusnog preseka sa osama zovu se temena konusnog preseka.

5) Tangenta. Tangenta u tački (x0 , y0 ) konusnog preseka je prava koja prolazi kroz tu tačku paralelno tetivama konjugovanim sa prečnikom koji takođe prolazi kroz tačku (x0 , y0 ).

Prečnik koji je spregnut sa pravcem k ima jednačinu

  fx’ + fy’ k = 0,

a jednačina tangente TT’ je jednačina pravekoja prolazi kroz tačku
(x0 , y0 ) i ima ugaoni koeficijent k, tj.

 y – y0 = k ( x - x0 ).

Pošto i prečnik prolazi kroz istu tačku (x0 , y0 ) imamo sledeći identitet:

  fx0’ + fy0’ k = 0; k = fx0’ / fy0’.

Eliminacijom veličine k iz prethodnih jednačina dobijamo traženu jednačinu tangente:

 y - y0 = - fx0’ (x - x0 ) / fy0’ ,

 ( x - x0 ) fx0’ + ( y - y0)fy0’= 0.

Jednačinu tangente možemo napisati i u sledećem obliku:

 (a11 x0+ a12 y0+ a13 ) x +(a21 x0 + a22 y0 + a23 )y +(a31 x0 +a32 y + a33 )= 0.

6) Polara. Uočimo neku tačku P koja ne pripada konusnom preseku i kroz nju povučimo sečicu PM1M2. Nađimo na toj sečici tačku Qtako da nam par tačaka P i Q bude harmonijski konjugovan sa parom tačaka M1
i M2. Tada za tačke P i Q kažemo da su harmonijski konjugovane u odnosu na dati konusni presek.

Polarom konusnog preseka sa polom u tački P zovemo geometrijsko mesto tačaka harmonijski konjugovanih sa polom P u odnosu na dati konusni presek.

Jednačina polare se dobija u sledećem obliku:

a11 x0 x + a12 ( y0 x + x0 y)+ a22 y0 y + a13 (x+ x0)+ a23 ( y+ y0 )+ a33 = 0,

gde su x0  i y0  koordinate pola  P. Jednačina polare je ista po obliku kao i jednačina tangente, razlika je u tome što su u jednačini tangente veličine x0  i y0  koordinate tačke na krivoj , a kod polare to su koordinate neke tačke koja nije na krivoj, koordinate pola.

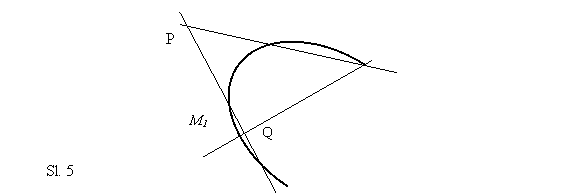
7) Asimptota. Asimptota konusnog preseka je prava koja dodiruje presek u beskonačnoj tački.

Eliminacijom veličine y iz jednačine konusnog preseka (12) i jednačine prave
 y = mx+ n (18)

dobićemo kvadratnu jednačinu po x

 A x2 + 2Bx +C = 0,

gde su uvedene oznake
 A ≡ a11 + 2a12 m + a22 m2,
 B ≡ ( a12  + a22 m) n + a23 m + a13 ,
 C ≡ a22 n2 +2 a23 n + a33 .

Da bi prava dodirivala krivu ova kvadratna jednačina mora da ima dvostruki koren, tj. mora da postoji uslov

B2 – AC = 0,
a da bi jednačina važila za x teži ∞ mora biti I
A = 0.
Ova dva uslova mogu se napisati u obliku

 A = 0, B = 0, ili
a11 + 2a12 m + a22 m2 = 0,
 ( a12  + a22 m) n + a23 m + a13 = 0,

i daju nam takve vrednosti za m i n (ako su realne ) na osnovu kojih jednačina (18) predstavlja traženu jednačinu asimptote.

8) Žiže i direktrise.

Označimo sa F (α, β) žižu, a sa DD’ :
 m1 x + n1 y + k1 = 0

direktrisu, sa M(x, y) ma koju tačku konusnog preseka, onda imamo
m/ d=e,

gde smo sa moznačili odstojanje tačke od žiže, a sa d odstojanje od direktrise. Poslednju jednačinu možemo napisati u obliku

 [ (x - α) 2+ (y - β) 2 ] 1/2 ; ( m1 x + n1 y + k1 ) / (m12+ n12) 1/2 = e
ili
(x - α) 2+ (y - β) 2 = ( m x +  n y + k) 2 , (19)

gde smo uveli oznake
m ≡ m1 e / (m12+ n12) 1/2 ,
 n ≡ n1 e / (m12+ n12) 1/2 ,
 k ≡ k1 e / (m12+ n12) 1/2 .

Jednačina (19), kao jednačina konusnog preseka, može da se razlikuje od jednačine (12) samo konstantnim množiteljem, recimo σ, i zato su odgovarajući koeficijenti ovih dveju jednačina proporcionalni:

(1- m2 ) / a11= mn / a12 = (1-n 2) / a22 = (a + km) / a13 = (β + kn) / a23
=( α2 + β2 - k2) / a33 (=σ). (20)

Ovih pet jednačina (20) služe za određivanje pet veličina α, β, m, n, k, tj. za određivanje žiža i direktrisa pomoću koeficijenata jednačine (12).

LITERATURA

[1] D. E. SMITH, History of Mathematics, Dover, 1958.

[2] DIRK J. STROJK, Kratak pregled istorije matematike, 1991.

[3] Dr BORIVOJE RAŠAJSKI, Analitička geometrija, 1960.

[4] N. BLAŽIĆ, N. BOKAN, Z. LUČIĆ, Z. RAKIĆ, Analitička geometrija, 2002.

 preuzmi seminarski rad u wordu » » » 

Besplatni Seminarski Radovi