Arhimed Arhimed, jedan od najgenijalnijih matematičara svih vremena, rodio se 287.godine pre nove ere u Sirakuzi. Podstaknut znanjem svog oca, Fidija, koji je inače bio astronom i matematičar, Arhimed je išao kroz život uvek iznova tragajući za novim znanjem. Njegov duh tražio je učenje koje mu niko nije mogao pružiti u Sirakuzi. Zato Arhimed kreće na školovanje u Aleksandriju, tadašnji kulturni centar sveta. Radeći u Aleksandrijskoj biblioteci, tada najvećoj riznici knjiga u Sredozemlju, Arhimed je izučio i usavršio mnoga znanja iz različitih oblasti nauke. Upoznao je puno mladih, sposobnih matematičara među kojima je bio i Eratosten, budući Arhimedov prijatelj. Međutim, u Aleksandriji Arhimed nije postao ono što je želeo i što su najčešće postajali daroviti matematičari, pesnici i medicinari - dvorski čovek koji će kroz svoja dela veličati vladajuću kuću. Njega je pre svega i jedino zanimala matematika.
Arhimed je živeo za matematiku i od matematike. U vreme rada na problemima, nije video ništa drugo. On je zaboravljao na jelo i prilike u kojima je radio. „Heureka! Heureka!“ (grč. prefiks glagola heursiko - nađem, izračunam, izmislim) „Našao sam!“, uzviknuo je Arhimed kada je, sedeći u kupatilu, otkrio fizički zakon da svako telo, potopljeno u tečnost, gubi od svoje težine onoliko kolika je težina njime istisnute tečnosti (ili gasa). Taj gubitak je u stvari potisak tečnosti ili gasa.
Vrativši se u Sirakuzu, Arhimed se u početku bavio astronomijom. Sirakuza nije dugo mogla uživati svoju slobodu te se stoga Arhimed spremao za odbranu svoga grada kako je znao i umeo. Mnoge legende govore o njegovim izumima koje je konstruisao u tu svrhu. Priča se da je konstruisao pokretne platforme za ispuštanje teškog kamenja i ključalog materijala na neprijateljske brodove ukoliko bi se suviše približili gradskim zidinama. Takođe se priča da je Arhimed konstruisao paleće ogledalo u obliku paraboloida pomoću koga su paljeni neprijateljski brodovi. Uz pomoć znanja iz fizike i matematike moguće je izračunati da je dužina latus rectum-a (prave linije koja prolazi kroz žižu ortogonalno na osu) jednaka parametru p u jednačini parabole y2=px. Kako se žiža parabole y2=px nalazi u tački (p/4, 0), pod pretpostavkom da se neprijateljski brod nalazi na 50 metara od gradskih zidina i da je smešten tačno u žižu Arhimedovog ogledala. Dakle, na p/4=50 metara ispada da bi prečnik ogledala morao da iznosi p=200 metara. Izvesno je da u to vreme (a i danas) nije bilo moguće napraviti ogledalo ovih razmera.
Najveću slavu, Arhimed je stekao svojim raspravama o zaobljenim geometrijskim telima. Izračunao je opseg i površinu kruga, površinu odsečka parabole, obim kugle, površinu elipse itd. Pri tom se služio metodama kojima se danas služimo u diferencijalnom i integralnom računu, tako da se Arhimed može smatrati tvorcem integralnog računa. Našao je način za pisanje vrlo velikih brojeva. Pokazao je kako se matematika može primeniti na mehaniku, otkrio zakone poluge, uzgona (tzv. Arhimedov zakon), određivanje težišta, izumeo vijak, unapredio statiku, postaviio osnove hidrostatike i odredio približnu vrednost broja . Arhimed je znao da ne postoji takav teret koji se ne može podići i najslabijom silom, samo ako se iskoristi poluga. Dovoljno je delovati tom malom silom na jedan krak veoma dugačke poluge i pustiti da onaj drugi, kratki krak, deluje na teret. Zato je bio siguran da bi on mogao snagom svoje ruke, a pritiskajući na jako dugačak krak neke poluge, podići čak i takav teret čija je masa jednaka masi naše Zemlje.
Međutim, da je znao kolika je masa naše planete, čak bi se i veliki mozak, kakav je bio Arhimed, morao zamisliti. Za takvu radnju – podizanje Zemlje za makar 1 cm trebalo bi mu trideset hiljada biliona godina.

Masa Zemlje se zna: 6.000.000.000.000.000.000.000.000 kg . Ako čovek može da podigne jednom rukom samo 60 kg, onda bi mu, da "podigne Zemlju" bilo potrebno da pritisne na duži krak poluge koji je duži od onog kraćeg kraka 100.000.000.000.000.000.000.000.000 puta. Prost račun će nam pokazati da bi za podizanje kraćeg kraka za samo 1 cm, duži krak mora da opiše u vasioni ogroman luk od 1.000.000.000.000.000.000.000 km.
Kakav neshvatljiv put bi morala da pređe Arhimedova ruka da bi podigla Zemlju za samo 1 cm. Ako uzmemo da Arhimed može podići 60 kg na visinu od 1 m za 1 sekundu (to je jedna konjska snaga!), onda mu je za podizanje Zemlje na visinu od 1 cm potrebno 1.000.000.000.000.000.000.000.000 sekundi ili tačno 30.000 biliona godina. Za ceo život Arhimed ne bi uspeo da Zemlju pomeri ni za dlaku. Kada bi čak i uspeo da brzinu svoje ruke poveća do brzine svetlosti, 300.000 km/sec, podiga bi Zemlju za 1 cm tek za 10.000.000 godina.

Ovaj veliki matematičar bio je vrstan polemičar ali i samokritičan. Na jednom mestu, kritikovajući neke svoje radove i greške, Arhimed piše: “Neka to bude zastrašujući primer kako se ljudi koji tvrde da tobože znaju da dokažu sve ono što predlažu drugima, a ne prilažu vlastita rešenja, moraju se na kraju krajeva uveriti kako su se latili da dokažu ono što nije moguće dokazati.
Podjednako je bio uspešan i u teorijskom i u praktičnom radu i u njihovom povezivanju. Sačuvana su njegova dela: O sferi i cilindru, Merenje kruga, O konoidima i sferoidima, O spiralama, Kvadratura parabole, O ravnoteži ravnih likova, O plivajućim telima.

O sferi i cilindru

Poznatu teoremu iz stereometrije, koja se može dobiti iz osobine ravnoteže, otkrio je Arhimed i uključio je u svoje čuveno delo “O sferi i cilindru”.
Ova teorema glasi: Količnik zapremina pravog kružnog cilindra, čija je visina jednaka njegovom prečniku i sfere upisane u taj cilindar iznosi 3:2, što je takođe jednako količniku njegovih površina.

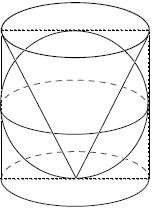
Ovo je bila jedna od najomiljenijih Arhimedovih teorema i na njegov zahtev bila je ugravirana na njegov nadgrobni spomenik.
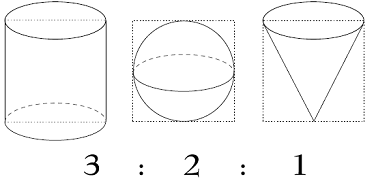
Euklid je u svojim Elementima dokazao da je zapremina valjka tri puta veća od zapremine kupe sa gore navedenim dimenzijama. Arhimed je dokazao da je zapremina sfere dve trećine zapremine valjka. Pa iz ova dva dokaza imamo da je se zapremine kupe, lopte (koje su upisane u valjak) i valjka odose kao 1:2:3.

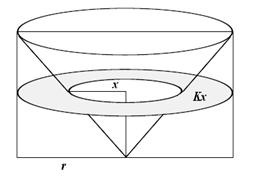
Dokaz: Neka su dati valjak i kupa prečnika osnove r i visine 2r i sfera prečnika r. Kupa i sfera su upisane u valjak. Ovako dobijeno telo presečemo nekom ravni na proizvoljnoj visini. Presek te ravni sa valjkom i kupom su dva koncentrična kruga. Prečnik kruga valjka je r, a prečnik kruga kupe označimo sa x.

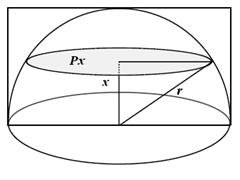
Površinu koju dobijemo kada od kruga valjka oduzmemo krug kupe označimo sa , gde je . Od sredine valjka odmerimo dužinu i na toj visini konstruišemo ravan koja je paralelna sa ravni osnove. U preseku te ravni i sfere dobijamo krug perčnika po Pitagorinoj teoremi. Površinu tog kruga označimo sa i ta površina iznosi . Iz ovih jednakosti vidimo da je za svako .

Sada ćemo za prvu presečnu ravan uzeti ravan osnove tela. Sledeća ravan kojom ćemo preseći telo je ravan na visini od osnove tela, naredna na visini (<) i tako dok ne stignemo do druge osnove tela primenjujući gore navedeni postupak Zbir svih dobijenih površina približno je jednak dve trećine zapremine valjka, a zbir svih površina približno je jednaka zapremini sfere. Što su delta-iksovi manji tačnost je veća. Znamo da je pa je . Ovim je dokaz završen.

Merenje kruga

Knjiga “Merenje kruga” nije sačuvana u originalnom izdanju i sastoji se iz samo tri proporcije. U njoj saznajemo da je Arhimed, primenjujući „metod iscrpljivanja”, prvi u istoriji matematike odredio približnu vrednost broja , a time i dužinu kružnice. To je učinio tako što je određivao odnos obima upisanih i opisanih pravilnih mnogouglova i prečnika odgovarajuće kružnice. Bitno je da kružnica bude jedinična jer je samo u tom slučaju površina kruga koju ona određuje jednaka . Računanje počinje koristeći graničnu vrednost √3, koju uzima kao poznatu, tj.

Arhimed je prvi razmatrao slučaj opisanog poligona.
Neka je CA tangenta u tački A na krug k(O, OA). Napravimo ugao AOC koji je jedna trećina pravog ugla, tj. p/6.

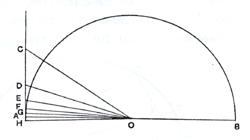Merenje kruga OD - bisektrisa ugla AOC,
OE - bisektrisa ugla AOD,
OF - bisektrisa ugla AOE,
OG - bisektrisa ugla AOF.

Ako je AH = AG, onda je <GOH=<FOA=p/24, pa je GH luk pravilnog 96-tougla.

OA : AC [ = √3 : 1] > 256: 153
OC : CA = 2 : 1 = 306 : 153.

Pošto OD polovi <COA, onda je

CO : OA = CD : DA
(CO + OA) : OA = CA : DA
ili
(CO + OA ) : CA = OA : AD.
Odatle sledi da je OA : AD > 571 : 153.

I OD2 : AD2 = (OA2 + AD2) : AD2
> (5712 + 1532) : 1532
> 349450 : 23409.

Zato Arhimed kaže da je OD : DA > 591 i 1/8 : 153.

Sada, kao što smo našli odnos OD : AD iz OC : CA i OA, analogno dobijamo odnos OA : AE i OE : AE iz OD : DA i OA : AD. Na kraju dobijamo odnos
OA : AG.

Izučavajuci upisani poligon, Arhimed dobija analogan sled aproksimacija. Neka tačke A, B, C obrazuju polukrug i neka je <BAC =p /2. Kako je
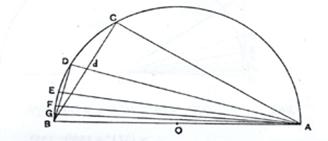AD - bisektrisa ugla BAC,
AE – bisektrisa ugla BAD,
AF – bisektrisa ugla BAE,
AG – bisektrisa ugla BAF,

prava BG obrazuje luk upisanog 96-tougla.

Uočimo sledeću sličnost:
Δ ADB ~ Δ BDd ~ Δ ACd.
Zato je AD : DB = BD : Dd = AC : Cd
= AB : Bd ( posto AD sece < BAC )
= (AB + AC) : (Bd + Cd)
= (AB + AC) : BC

Ali, AC : CB < 1351 : 780
i
BA : BC = 2 : 1 =1560 : 780
pa je
AD : DB < 2911 : 780.

Odavde je AB2 : BD2 < (29112 + 7802) : 7802
< 9082321 : 608400
i po Arhimedu
AB : BD < 3013 ¾ : 780.

Kao što smo našli odnos AB : DB i AB : BD i AC : CB, analogno dobijamo odnos AE : EB i AB : BE iz AB : BD i AD : DB i na kraju odnos AB : BG.

Razlikujemo dva slučaja i u njima dva uslova a0,a1,a2,...,an i b0,b1,b2,...,bn gde je
a1 = a0 + b0,
a2 = a1 + b1, ...

b1 = √(a12 + c2),
b2 = √(a22 + c2),...

U prvom slucaju a0 = 265, b0 = 306, c = 153,
a u drugom je a0 = 1351, b0 = 1560, c = 780.

U prvom slucaju, odnos a4 : c je zapravo odnos OA : AG = 2OA : GH,
a u drugom b4 : c je odnos AB : BG. GH u prvom i BG u drugom slučaju se lukovi pravilnog upisanog 96-tougla odnose naizmenično pa konačno imamo

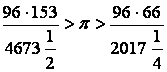
Arhimed iz ovoga zaključuje da je

.
U stvari, važi da je 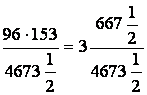, i .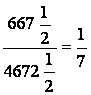
Takođe je zaključio da 3 10/71 = 3 + 1/7 + 1/10 i da se to može predstaviti kao 6336/2017 ¼.
Treba napomenuti da, u tekstu koji imamo, vrednosti b1, b2, b3, b4 su oblika u njihovoj konačnoj formi bez međukoraka razmatrajući temeljno prvi slučaj, gde smo rekli da je OD2 : AD2 > 349450 : 23409 i onda je OD : DA > 591 1/8 : 153.
Arhimed figuru dobija kao aproksimaciju kvadratnog korena u oba slučaja ili koristeći metodu do koje je sam došao.
Pokazali smo da je Arhimed, u saglasnosti sa Heronom, napravio zatvoreniju aproksimaciju vrednosti broja p.

Arhimedov zavrtanj i Arhimedova spirala

Arhimedov zavrtanj i Arhimedova spirala
Arhimed je poznat po svojim mnogobrojnim izumima. Jedan od njegovih izuma još uvek se koristi u raznim delovima sveta. To je takozvani Arhimedov zavrtanj. On se sastoji od cevi, otvorene na oba kraja, koja je

kružno obavijena oko centralne cilindrične osovine formirajući zavojnicu poput vadičepa. Jedan kraj cevi je potopljen u vodu dok je osovina zavrtnja nagnuta pod dovoljno velikim uglom u odnosu na vertikalu. Prava se zatim okreće oko ose pomoću ručice na gornjem kraju osovine. Ukoliko je nagib osovine dovoljno veliki, voda će teći kroz cev i izlaziti na gornjem kraju. Arhimedov zavrtanj se koristio u starom Egiptu za navodnjavanje polja kao i za isušivanje močvarnih predela. Takođe je često korišćen za pražnjenje vode iz trupa broda.

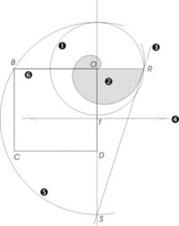
Arhimedova spirala je transcedentna krivulja koja nastaje kad tačka, polazeći iz odredišta, jednako obilazi odredište i jednako se udaljava od njega. Udaljenost svake tačke Arhimedove spirale od odredišta proporcionalna je uglu zaokreta. Prvi ju je otkrio Konon ali je Arhimed izučio njene brojne osobine, među kojima je problem kvadrature kruga, pa stoga spirala nosi njegovo ime.

Kvadratura parabole

Najraniji zabeleženi primer konvergentnog geometrijskog reda čija je suma bila poznata je red :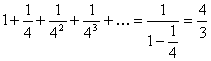

Ovaj red je koristio Arhimed (oko 225.god. pre nove ere) u svojoj kvadraturi parabole. Arhimed metodom beskrajnog uzastopnog približavanja dolazi do površine (do takozvane kvadrature) odsečka parabole. Ta metoda je dobila svu svoju vrednost tek pronalaskom infinitezimalnog (diferencijalnog i integralnog) računa. Beskrajnim približavanjem dolazimo do tzv. graničnih
vrednosti , a pojam granične vrednosti ili granice je osnovni stub infinitezimalnog računa i uopšte „više matematike“. U tim stvarima Arhimed je, dakle, jedan od prethodnika infinitezimalnog računa.
Evo kako on dolazi do kvadrature parabole. Da bi dobio površinu odsečka omeđenog tetivom

, Arhimed povuče prvo duž

kroz središte

tetive

, paralelno osi parabole. Označimo površinu trougla

slovom

. Ona se lako izračunava čim su date tačke

na paraboli. Ako na tetivama

sagradimo analogno trouglove

, polazeći od središta

tih tetiva, imamo dva nova trougla, oba manja od prvoga. Jednostavnim geometrijskim posmatranjem nalazimo da je površina svakog od ta dva trougla

, dakle, da je površina oba zajed no

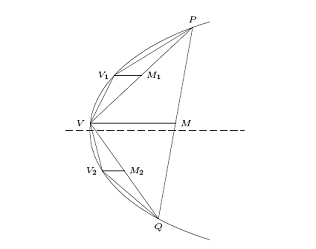
Da bi dobio površinu odsečka parabole Arhimed nastavlja započeto raspolovljavanje tetiva beskrajno i dobija tako, između lukova parabole i dvaju trouglova i , prvo četiri još manja trougla kojima je ukupna površina, kao što se odmah uviđa, opet četvrtina površine prethodana dva trougla, tj.

Zatim dobija osam još manjih trouglova s ukupnom površinom

itd. Prema tome, površina uočenog odsečka parabole ima vrednost beskrajnog zbira

To je geometrijski red (beskrajne zbirove nazivamo redovima, a članovi tog reda sačinjavaju geometrijsku progresiju) i imamo da je

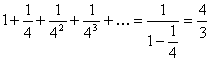
pa je , a time je problem rešen.

Arhimedov zadatak - Krznarski nož

Krznarski nož ima oblik figure koju određuju tri polukruga koji se dodiruju kao na slici i čiji su centri kolinearni. Dokazati da je površina krznarskog noža jednaka površini kruga čiji je prečnik upravan na pravu određenu centrima polukrugova, a pruža se, kao na slici, od tačke dodira manjih polukrugova do preseka sa najvećim polukrugom.
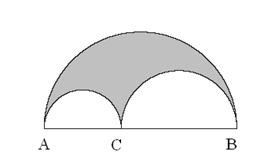
Arhimedov zadatak
Dokaz: je prečnik velikog polukruga, i su prečnici manjih polukrugova. Površina krznarskog noža dobija se tako što se od površine velikog polukruga oduzme zbir površina manjih polukrugova, tj.

Dalje važi: , odnosno .
Zatim, je prav (kao ugao nad prečnikom), pa je trougao pravougli (sa pravim uglom kod temena ). Tačka je podnožje upravne iz na pravoj . Pravougli trouglovi i (uz normalu) su slični (na osnovu II stava o sličnosti trouglova) :
(jer su oba prava),
(kao uglovi sa normalnim kracima: , ),
pa mora biti i .
Zato važi : , tj. .

Sada je :
, a to je upravo površina kruga čiji je prečnik .

Arhimedova smrt

Arhimedova smrt poznata je, u okvirima koji su do nas stigli, zahvaljujući Plutarhovom životopisu vojskovođe Marcellus. Poginuo je od mača rimskog vojnika u rodnom gradu Sirakuzi, koja je odolevala Rimljanima zahvaljujući spravama i mašinama, koje je Arhimed sastavio od poznatih jednostavnih alata. Kada je Sirakuzu, nakon dve godine, zauzeo Marcellus, Plutarh kaže, da je rimski vojskovođa dao nalog da se zaštiti Arhimed. Rimski vojnik ga nije prepoznao i ubio ga je 212. godine pre nove ere. Legenda kaže da je Marcellus bio ogorčen na vojnika koji je ubio Arhimeda.
Prema Valeriju Maksimu, prilikom zauzeća Sirakuze, Arhimed je mirno crtao geometrijske slike i doviknuo rimskom vojniku: „Noli turbare circulos meos” („Nemoj kvariti moje krugove”). Vojnik, smatrajući da ove reči vređaju moć pobednika, odsekao mu je glavu i Arhimedova krv poprskala je njegov znanstveni rad. Ali ovo je samo legenda jer je teško poverovati da se Arhimed mogao razumeti s Rimljaninom jer je on govorio grčki, a vojnik latinski. Pored toga Rimljani su zverski kažnjavali pobeđene, a naročito je Marcellus u tome bio svirep. On je čak naređivao da se pobiju žene i deca kada bi neki grad narušio ugovor koji je imao s Rimom.
Sirakužani nisu smeli održavati grob svog velikog mislioca. Njega je jedva pronašao Ciceron i to zahvaljujući crtežu lopte i valjka koji se nalazio na spomeniku iznad nekoliko stihova urezanih velikom matematičaru u spomen. „Odmah sam rekao predstavnicima Sirakuze koji su me pratili da je pred nama bez sumnje Arhimedov nadgrobni spomenik. I zaista, čim su pozvali ljude da iseku korov i da nam prokrče put i čim smo približili ovom stubu, videli smo u njegovom podnožju natpis. Deo uklesanih stihova mogao se još pročitati, sve ostalo je satrlo vreme.” I tako, jedan od najslavnijih gradova Grčke, koji je nekada dao svetu toliko velikana, nije više znao čak ni gde se nalazi grobnica najgenijalnijeg njegovog građanina se dok se nije pojavio čovek iz malog grada Arpina, da bi im pokazao taj grob!
Arhimed

Zanimljivo je da je Arhimedova želja bila da na njegovom grobu bude podignut spomenik, na kojem će biti dva geometrijska tela: valjak i lopta.

Malo ljudi je bilo sposobno da razume Arhimeda, a mnogi su imali koristi od njegovog znanja. Zato nije nikakvo čudo što je jedan matematičar čak iz XVII veka rekao: „Arhimeda više hvale nego sto ga čitaju, više se ponose njime nego što ga razumeju”.

Jedinstveni zaključak koji se može izvući o radu i delu Arhimeda je da je on najveći matematičar i naučnik antičkog doba i jedan od tri najveća matematičara svih vremena zajedno sa Isakom Njutnom i Karl Fridrih Gausom. Arhimed se izdigao do veličine koja je nadvisila sve druge naučnike antike.

Literatura:

[1] Miodrag Petković, Ljiljana Petković, Matematički vremeplov, Zmaj, Novi Sad 2006.
[2] Borisav Simić, I to je matematika, Zavod za udžbenike i nastavna sredstva, Beograd 1992.
[3] Boris Čekrlija, Vremeplovom kroz matematiku, Grafid, Banjaluka 2000.
[4] Miloš Radojčić, Opšta matematika-Matematika Egipta, Mesopotamije i Stare Grčke
[5] Lanselot Hogben, Stvaranje matematike, Vuk Karadžić, Beograd 1972.god.
[6] Архимед сочинения, Государственное издателъство физико-математической литературы, Москва 1962.год.

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi