OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
HROMATSKI BROJ I POPLOČAVANJE RAVNI
Upoznaćemo se sa jednim problemom iz kombinatorne geometrije, koji je
zbog svoje elegancije i prividne jednostavnosti tokom više od pola veka
zaokupljao umove mnogih slavnih matematičara. Premda do danas nije rešen,
doprineo je razvoju mnogih matematičkih disciplina, od kombinatorike (npr.
teorija grafova, Ramseyeva teorija) do geometrije (npr. popločavanja,
pakovanja), a neki mu aspekti zadiru i u pitanja matematičke logike.
Problem je prvi postavio 18-godišnji Edward Nelson 1950. godine premda
su do njega nezavisno došli P. Erdös i H. Hadwiger. Među ostalim poznatim
matematičarima koji su se bavili ovim problemom nalaze se i R. Graham
i E. Szemeredi. Spominje ga i M. Gardner 1960. godine u svojoj kolumni
Matematičke igre popularnog časopisa Scientific American.
U posljednjih 50-ak godina o problemu je napisano nekoliko desetina naučnih
radova. Demonstriraćemo tipični put matematičkog istraživanja: kako jedan
zanimljiv problem evoluira u mnoge druge, kako se raznovrsne matematičke
teorije međusobno obogaćuju i kako je u matematičkom istraživanju moguće
ostvariti važan napredak, a da se uopšte ne odgovori na prvobitno postavljeno
pitanje.
2. Formulacija problema i osnovni rezultati
Evo osnovnog problema:
Koliko je najmanje boja potrebno da bismo obojili sve tačke ravni tako da nikoje dve isto obojene tačke ne budu međusobno udaljene tačno za 1?Najmanji potrebni broj boja zvaćemo hromatski broj ravni i označivati sa
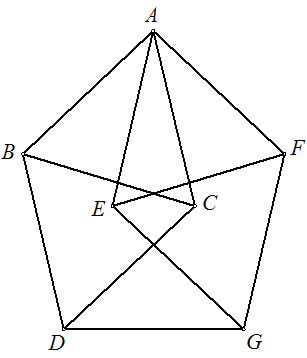
Zaista, pretpostavimo da je ![]() , tj. da postoji pravilno bojenje u 3 boje. Iz jednakostraničnih trouglova
na slici zaključujemo da su tačke A i D iste boje, a isto tako tačke A
i G, ali to nije moguće jer su D i G udaljene za 1. Dakle,
, tj. da postoji pravilno bojenje u 3 boje. Iz jednakostraničnih trouglova
na slici zaključujemo da su tačke A i D iste boje, a isto tako tačke A
i G, ali to nije moguće jer su D i G udaljene za 1. Dakle, ![]() .
.
S druge strane, nije odmah jasno da je pravilno bojenje (u konačno mnogo boja) uopšte moguće. Ipak, nakon malo isprobavanja lako dolazimo do sledećeg pravilnog bojenja u 7 boja:

Boje se ponavljaju periodično. Drugi način gledanja na gornju sliku jeste da uočimo ponavljanje "cvetnog uzorka":

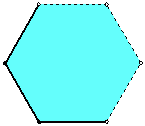
Pravilni šestouglovi na slici imaju stranicu dužine ![]() . Osim toga, svakom šestouglu uključujemo tri stranice i dva vrha, kako
je prikazano na slici, a isključujemo ostale tačke ruba. (To je potrebno
da bi šestouglovi zaista činili particiju ravni.)
. Osim toga, svakom šestouglu uključujemo tri stranice i dva vrha, kako
je prikazano na slici, a isključujemo ostale tačke ruba. (To je potrebno
da bi šestouglovi zaista činili particiju ravni.)
Uzmimo sada npr. dve crvene tačke. Ako pripadaju istom šestouglu,
onda su udaljene za manje od 1 (koliko je duga najveća dijagonala šestougla),
a ako pripadaju različitim šestouglovima, udaljenost im je veća od ![]() . Dakle, zaista nikoje dve tačke iste boje nisu udaljene za 1. Time smo
pokazali da je 7 boja dovoljno premda bismo možda mogli proći i ekonomičnije.
U svakom slučaju, dokazali smo osnovni rezultat:
. Dakle, zaista nikoje dve tačke iste boje nisu udaljene za 1. Time smo
pokazali da je 7 boja dovoljno premda bismo možda mogli proći i ekonomičnije.
U svakom slučaju, dokazali smo osnovni rezultat:
![]() ,
tj.
,
tj. ![]() je 4, 5, 6, ili 7.
je 4, 5, 6, ili 7.
Zvuči neverovatno, ali do danas nije poznato ništa više
o samom broju ![]() ,
tj. još uvek imamo četiri mogućnosti. Neki su matematičari čak javno iznosili
svoje mišljenje o broju
,
tj. još uvek imamo četiri mogućnosti. Neki su matematičari čak javno iznosili
svoje mišljenje o broju ![]() , naravno, bez strogog dokaza.
, naravno, bez strogog dokaza.
Drugi primer pravilnog bojenja u 7 boja jeste ovo šareno popločavanje ravni kvadratima:

Kvadrati imaju stranicu dužine ![]() , a svaki red kvadrata dobija se iz gornjeg reda translacijom ulevo za
vektor dužine
, a svaki red kvadrata dobija se iz gornjeg reda translacijom ulevo za
vektor dužine ![]() . Svakom kvadratu uključujemo levu i donju stranicu i donji levi vrh,
a oduzimamo mu ostale tačke ruba.
. Svakom kvadratu uključujemo levu i donju stranicu i donji levi vrh,
a oduzimamo mu ostale tačke ruba.

3. Pokušaji popravljanja donje granice
S obzirom da nije poznato pravilno bojenje ravni u manje od 7 boja,
mnogi su matematičari pokušali popraviti donju procenu 4 za broj potrebnih
boja. Prirodno je proučavati takva bojenja gde skupovi koje čine sve tačke
iste boje imaju još neko lepo svojstvo. Ako od bojenja još zahtevamo da
bude merljvo (tj. da čini particiju ravni na Lebeg-merljve skupove), onda
je potrebno koristiti barem 5 boja. Drugim rečima, merljivi hromatski
broj ravni je barem 5.
Svaki podskup ravni koji "konstruktivno zadamo" (ovde to znači:
bez korišćenja aksioma izbora) biće Lebeg-merljiv. To znači da ako pravilno
bojenje u 4 boje uopšte postoji, sigurno ga nećemo moći nacrtati, tj.
izgledaće (barem u nekom svom delu) otprilike ovako:

Već ovaj rezultat pokazuje koliko je problem logički suptilan. Naime,
izostavljanjem aksioma izbora moguće je konstruisati model teorije skupova
u kome je svaki podskup ravni Lebeg-merljiv pa u takvom "svetu"
važi ![]() . Ipak, većina matematičara živi i radi u Zermelo-Fraenkelovoj teoriji
skupova sa aksiomom izbora pa je za nas ipak moguće
. Ipak, većina matematičara živi i radi u Zermelo-Fraenkelovoj teoriji
skupova sa aksiomom izbora pa je za nas ipak moguće ![]() . Ako od skupova određenih bojama tražimo da budu "još lepši",
onda je za dobro bojenje potrebno koristiti barem 6 boja.
. Ako od skupova određenih bojama tražimo da budu "još lepši",
onda je za dobro bojenje potrebno koristiti barem 6 boja.
4. Pokušaji popravljanja gornje granice
U prethodnoj tački videli smo ozbiljna ograničenja koja srećemo kad
želimo pravilno obojiti ravan u 4 ili 5 boja. Ipak, nađena su neka "gotovo
pravilna" bojenja ravni u 6 boja, koja sugerišu da možda važi ![]() .
.
Za bojenje ravni u k boja kažemo da je tipa ![]() ako nikoje dve tačke boje i nisu udaljene za
ako nikoje dve tačke boje i nisu udaljene za ![]() ,
i = 1,...,m. Egzistencija 6-bojenja tipa (1,1,1,1,1,1) značila
bi
,
i = 1,...,m. Egzistencija 6-bojenja tipa (1,1,1,1,1,1) značila
bi ![]() .
Prilično smo blizu toga: nađeno je 6-bojenje tipa (1,1,1,1,1,
.
Prilično smo blizu toga: nađeno je 6-bojenje tipa (1,1,1,1,1,![]() ).
).

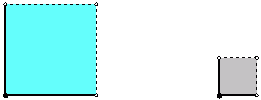
Siva boja na slici ne pokazuje udaljenost ![]() , a ostale boje ne pokazuju udaljenost 1. Osmouglovi imaju stranice dužine
, a ostale boje ne pokazuju udaljenost 1. Osmouglovi imaju stranice dužine
![]() i
i ![]() , a kvadratići imaju dužinu stranice
, a kvadratići imaju dužinu stranice ![]() .
.

Zanimljivo je i ovo 6-bojenje tipa (1,1,1,1,1,![]() ).
).

Dužina stranice svakog kvadrata je ![]() ili
ili ![]() .
.
5. Veza sa teorijom grafova i logikom sudova
Vreme je da koncept bojenja podignemo na formalno viši nivo. (Jednostavni
neusmereni) graf je uređeni par G = (V, E) skupa V i refleksne simetrične
binarne relacije E na skupu V. Elemente skupa V zovemo vrhovi grafa, a
elemente relacije E zovemo bridovi grafa pa kažemo da su dva vrha susedna
(ili da su spojena bridom) ako je taj par vrhova u relaciji E. (Primetimo
da prema našoj definiciji V i E mogu biti beskonačni iako se u teoriji
grafova najčešće proučavaju konačni grafovi.) Naprimer, označimo sa ![]() graf kome je skup vrhova
graf kome je skup vrhova ![]() , a dve tačke su susedne ako i samo ako su udaljene za 1.
, a dve tačke su susedne ako i samo ako su udaljene za 1.
Kažemo da je graf k-obojiv (k je prirodan broj) ako
mu je skup vrhova moguće podeliti u k podskupova (to su "boje")
tako da nikoja dva vrha iz istog podskupa nisu susedna. Hromatski broj
grafa G je najmanji k takav da je graf k-obojiv, a označavamo
ga sa ![]() . (Moguće je i da takav prirodni broj uopšte ne postoji.) Primetimo da
naš osnovni problem zapravo traži da izračunamo
. (Moguće je i da takav prirodni broj uopšte ne postoji.) Primetimo da
naš osnovni problem zapravo traži da izračunamo ![]() . Graf
. Graf ![]() može se prirodno nazvati ravan jediničnih udaljenosti pa stoga
može se prirodno nazvati ravan jediničnih udaljenosti pa stoga ![]() zovemo hromatski broj ravni. Radi jednostavnosti umesto
zovemo hromatski broj ravni. Radi jednostavnosti umesto ![]() pišemo
pišemo ![]() .
.
Podgraf grafa G = (V, E) je svaki graf G' = (V', E') takav da su V'
i E' redom podskupovi od V i E. Npr. Moserovo vreteno jedan je konačan
podgraf grafa ![]() .
Fundamentalni rezultat o bojenju beskonačnih grafova je de Bruijn-Erdös-eva
teorema:
.
Fundamentalni rezultat o bojenju beskonačnih grafova je de Bruijn-Erdös-eva
teorema:
Teorema: Graf je k-obojiv ako i samo ako je
svaki njegov konačni podgraf k-obojiv.
U vezi s našim problemom to znači da je dovoljno bojiti konačne konfiguracije
tačaka ravni. Tako bi, naprimer, za dokaz hipoteze ![]() bilo dovoljno dokazati da je svaki konačni skup tačaka ravni obojiv u
4 boje tako da nema tačaka istih boja udaljenih za 1. Ovaj pristup omogućava
primenu brojnih tehnika teorije (konačnih) grafova i dobjeni su neki parcijalni
rezultati, ali sama hipoteza nije ni dokazana ni opovrgnuta. Eventualni
nedostatak pristupa je to što se ova teorema dokazuje korišćenjem nekog
od ekvivalenata aksioma izbora i dokaz nije nimalo konstruktivan. Zato
čak i da uspemo dokazati kako je svaki konačan podgraf od
bilo dovoljno dokazati da je svaki konačni skup tačaka ravni obojiv u
4 boje tako da nema tačaka istih boja udaljenih za 1. Ovaj pristup omogućava
primenu brojnih tehnika teorije (konačnih) grafova i dobjeni su neki parcijalni
rezultati, ali sama hipoteza nije ni dokazana ni opovrgnuta. Eventualni
nedostatak pristupa je to što se ova teorema dokazuje korišćenjem nekog
od ekvivalenata aksioma izbora i dokaz nije nimalo konstruktivan. Zato
čak i da uspemo dokazati kako je svaki konačan podgraf od ![]() 4-obojiv, još uvek ne bismo znali "kako izgleda" neko dobro
4-bojenje cele ravni.
4-obojiv, još uvek ne bismo znali "kako izgleda" neko dobro
4-bojenje cele ravni.
Skicirajmo dokaz de Bruijn-Erdös-eve teoreme. On je direktna posledica teoreme kompaktnosti u logici sudova:
Teorema: Skup formula je ispunjiv ako i samo ako je svaki njegov konačni podskup ispunjiv.
Napomenimo samo da skup propozicionih varijabli iz alfabeta logike sudova ne mora biti prebrojiv, a teorema kompaktnosti važi i u toj opštosti. Potrebno je samo malo modifikovati dokaz i iskoristiti neku ekvivalentnu aksiomu izbora, npr. Zornovu lemu.
Dakle, neka je G = (V, E) graf i pretpostavimo da je svaki njegov konačni
podgraf k-obojiv. Posmatramo logiku sudova kojoj je skup propozicionih
varijabli jednak V ![]() {1,2,...,k}. Označimo s
{1,2,...,k}. Označimo s ![]() skup koji sadrži sledeće formule:
skup koji sadrži sledeće formule:
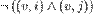 ,
za svako
,
za svako 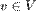 i svako
i svako 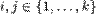 ,
, 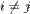 ,
,
čitamo: "vrh v nije istovremeno obojen različitim bojama i i j"
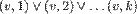 ,
za svako
,
za svako 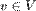 ,
,
čitamo: "vrh v je obojen barem jednom bojom"
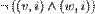 ,
za svaki
,
za svaki 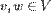 ,
, 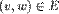 i svako
i svako 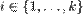 ,
čitamo: "susedni vrhovi v i w nisu obojeni istom
bojom i".
,
čitamo: "susedni vrhovi v i w nisu obojeni istom
bojom i".
Želimo da pokažemo da je skup ![]() ispunjiv, tj. da postoji interpretacija I koja sve formule iz
ispunjiv, tj. da postoji interpretacija I koja sve formule iz
![]() valuira kao "istina". Tada ćemo vrh v obojiti bojom
i ako i samo ako je I (v, i) = "istina".
Zbog teoreme kompaktnosti dovoljno je pokazati da je svaki konačni podskup
od
valuira kao "istina". Tada ćemo vrh v obojiti bojom
i ako i samo ako je I (v, i) = "istina".
Zbog teoreme kompaktnosti dovoljno je pokazati da je svaki konačni podskup
od ![]() ispunjiv. Svaki konačni skup formula koristi samo konačno mnogo propozicionih
varijabli pa se u njemu pojavljuje konačno mnogo elemenata od V. Podgraf
od G generisan tim konačnim skupom vrhova po pretpostavci je k-obojiv.
Jedno njegovo dobro k-bojenje definiše vrednosti neke parcijalne
interpretacije koja valuira "istina" sve formule iz razmatranog
konačnog podskupa od
ispunjiv. Svaki konačni skup formula koristi samo konačno mnogo propozicionih
varijabli pa se u njemu pojavljuje konačno mnogo elemenata od V. Podgraf
od G generisan tim konačnim skupom vrhova po pretpostavci je k-obojiv.
Jedno njegovo dobro k-bojenje definiše vrednosti neke parcijalne
interpretacije koja valuira "istina" sve formule iz razmatranog
konačnog podskupa od ![]() , tj. on je ispunjiv.
, tj. on je ispunjiv.
6. Bojenje racionalnih tačaka
Racionalna tačka u ![]() je tačka kojoj su obe koordinate racionalni brojevi, tj. element od
je tačka kojoj su obe koordinate racionalni brojevi, tj. element od ![]() .
Takvih tačaka ima samo prebrojivo mnogo, dakle "mnogo manje"
nego svih tačaka ravni pa se možemo nadati da će hromatski broj podgrafa
biti manji nego hromatski broj celog grafa.
.
Takvih tačaka ima samo prebrojivo mnogo, dakle "mnogo manje"
nego svih tačaka ravni pa se možemo nadati da će hromatski broj podgrafa
biti manji nego hromatski broj celog grafa.
Teorema: Graf ![]() je bipartitivan pa je
je bipartitivan pa je ![]() .
.
Za graf kažemo da je bipartitivan ako mu se skup vrhova može rastaviti na dva podskupa tako da svaki brid spaja vrhove iz različitih podskupova. Drugim rečima, graf je bipartitivan ako i samo ako je 2-obojiv.
Skiciraćemo dokaz ove tvrdnje. Ciklus je put u grafu kome se podudaraju početak i kraj. Poznata König-ova teorema iz teorije grafova glasi:
Teorema: Graf je bipartitivan ako i samo ako nema ciklusa neparne dužine.
Pretpostavimo da u grafu ![]() postoji ciklus dužine 2k+1. To ima za posledicu da u ravni postoji 2k+1
vektora
postoji ciklus dužine 2k+1. To ima za posledicu da u ravni postoji 2k+1
vektora ![]() sa racionalnim koordinatama, dužine 1 i kojima je zbir
sa racionalnim koordinatama, dužine 1 i kojima je zbir
nula-vektor.
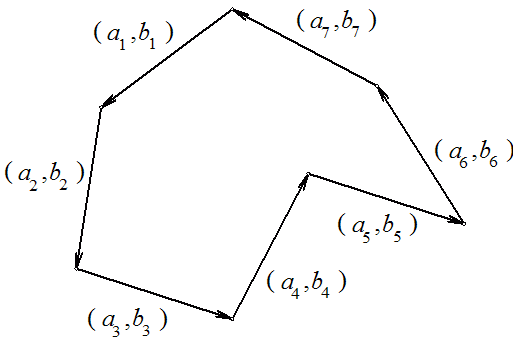
Iz teoreme o Pitagorinim trojkama sledi da su svi ti vektori oblika
![]() ili
ili ![]() za neke cele brojeve m i n koji su relativno prosti
i različite parnosti. Primetimo da razlomak
za neke cele brojeve m i n koji su relativno prosti
i različite parnosti. Primetimo da razlomak ![]() ima neparan broilac i imenilac pa da zbir 2k+1 takvih razlomaka opet ima
(i nakon eventualnog skraćivanja) neparan broilac i imenilac. Zato taj
zbir ne može biti 0. S druge je strane
ima neparan broilac i imenilac pa da zbir 2k+1 takvih razlomaka opet ima
(i nakon eventualnog skraćivanja) neparan broilac i imenilac. Zato taj
zbir ne može biti 0. S druge je strane ![]() , što je kontradikcija!
, što je kontradikcija!
7. Prava, ravan, 3D-prostor ...
Prirodna generalizacija našeg problema jeste određivanje hromatskog
broja n-dimenzionog euklidskog prostora ![]() .
.
Za pravu (n = 1) očigledno važi ![]() .
Tačke iz
.
Tačke iz ![]() jednostavno bojimo crveno za parne m, a zeleno za neparne.
jednostavno bojimo crveno za parne m, a zeleno za neparne.
![]()
Videli smo da u ravni već postoje problemi, a u većim dimenzijama oni
su još izraženiji. Tek nedavno su dobijene ocene ![]() , a u dimenzijama
, a u dimenzijama ![]() razmaci između donje i gornje granice su mnogo veći. Što se tiče procene
broja
razmaci između donje i gornje granice su mnogo veći. Što se tiče procene
broja ![]() za velike n, dokazano je
za velike n, dokazano je
![]() ,
kada
,
kada ![]() ,
,
što po definiciji znači
![]() .
.
U svakom slučaju, niz ![]() raste eksponencijalno.
raste eksponencijalno.
8. Da li je lakše obojiti sferu?
Označimo sa ![]() (dvodimenzionalnu) sferu u
(dvodimenzionalnu) sferu u ![]() poluprečnika r. Želimo naći
poluprečnika r. Želimo naći ![]() ,
tj. najmanji broj boja potreban za bojenje sfere tako da istobojne tačke
ne budu udaljene za 1. (Pritom udaljenost merimo euklidski, tj. onako
kako ih računamo u
,
tj. najmanji broj boja potreban za bojenje sfere tako da istobojne tačke
ne budu udaljene za 1. (Pritom udaljenost merimo euklidski, tj. onako
kako ih računamo u ![]() .) Kako r raste, zakrivljenost sfere
.) Kako r raste, zakrivljenost sfere ![]() sve je manja pa je ona lokalno sve sličnija ravni. Zato sa pravom očekujemo
da će se to odraziti i na njen hromatski broj.
sve je manja pa je ona lokalno sve sličnija ravni. Zato sa pravom očekujemo
da će se to odraziti i na njen hromatski broj.
Jedino što je poznato o hromatskim brojevima sfera jeste sledeća tablica.
U nju se uklapa i osnovni rezultat za ravan ako je shvatimo kao sferu
poluprečnika ![]() .
.
poluprečnik sfere |
donja granica |
gornja granica |
|
4 |
7 |
|
4 |
4 |
|
4 |
7 |
|
4 |
5 |
|
3 |
5 |
|
3 |
4 |
|
2 |
2 |
|
1 |
1 |
Uočimo da je sfera ![]() jedini netrivijalni slučaj iz gornje tablice za koji je poznat hromatski
broj,
jedini netrivijalni slučaj iz gornje tablice za koji je poznat hromatski
broj, ![]() . Definisaćemo jedno njeno pravilno bojenje u 4 boje. U tu svrhu koristićemo
sferne koordinate. Svaka tačka sfere određena je sa dva ugla:
. Definisaćemo jedno njeno pravilno bojenje u 4 boje. U tu svrhu koristićemo
sferne koordinate. Svaka tačka sfere određena je sa dva ugla: ![]() je ugao između pozitivnog dela z-ose i prave OT;
je ugao između pozitivnog dela z-ose i prave OT; ![]() je ugao između pozitivnog dela x-ose i projekcije te prave na xy-ravan.
je ugao između pozitivnog dela x-ose i projekcije te prave na xy-ravan.
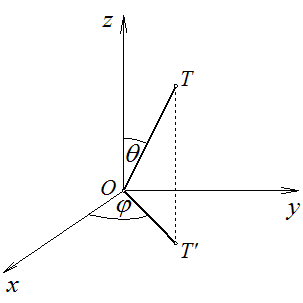
Primetimo da su tačke A i B na ![]() udaljene za 1 ako i samo ako je ugao
udaljene za 1 ako i samo ako je ugao ![]() prav. Tačke od
prav. Tačke od ![]() bojimo na sledeći način:
bojimo na sledeći način:
- Tačke za koje je
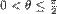 ,
, 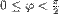 obojimo zeleno.
obojimo zeleno. - Tačke za koje je
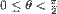 ,
, 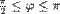 obojimo crveno.
obojimo crveno. - Tačke za koje je
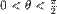 ,
, 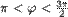 obojimo žuto.
obojimo žuto. - Tačke za koje je
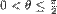 ,
, 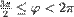 obojimo plavo.
obojimo plavo. - Sve ostale tačke obojimo kao njima antipodne (centralno simetrične u odnosu na centar).
Dakle, gornja polusfera sada izgleda ovako (gledana odozgo):
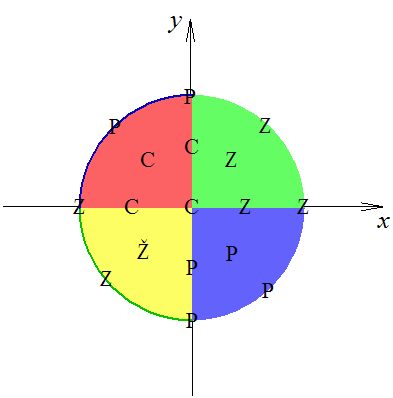
Lako se može proveriti da je ovo bojenje dobro, iz čega dobijamo ![]() . Obratnu nejednakost nešto je teže dokazati. Jedna evidentna poteškoća
je to što
. Obratnu nejednakost nešto je teže dokazati. Jedna evidentna poteškoća
je to što ![]() nema podgraf "izomorfan" Moserovom vretenu.
nema podgraf "izomorfan" Moserovom vretenu.
9. Bojenje metričkog prostora
Za bilo koji metrički prostor X = (X, d) možemo definisati
![]() kao najmanji broj boja potreban za bojenje skupa X tako
da ne postoje istobojne tačke
kao najmanji broj boja potreban za bojenje skupa X tako
da ne postoje istobojne tačke ![]() za koje bi važilo
za koje bi važilo ![]() .
Videli smo da određivanje
.
Videli smo da određivanje ![]() može biti vrlo težak problem. Na ovom (prevelikom) nivou opštosti zapravo
i nema korisnih rezultata osim de Bruijn-Erdös-ove teoreme.
može biti vrlo težak problem. Na ovom (prevelikom) nivou opštosti zapravo
i nema korisnih rezultata osim de Bruijn-Erdös-ove teoreme.
S druge strane, u pojedinim metričkim prostorima X broj
![]() vrlo je lako odrediti. Naprimer, neka je X =
vrlo je lako odrediti. Naprimer, neka je X = ![]() ,
ali sada uobičajenu euklidsku metriku
,
ali sada uobičajenu euklidsku metriku
![]() ,
,
![]()
zamenimo metrikom
![]() ,
,
![]() .
.
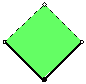
Nije teško videti da je ![]() . Jedno pravilno 4-bojenje izgleda ovako:
. Jedno pravilno 4-bojenje izgleda ovako:

Označene tačke elementi su celobrojne rešetke ![]() . Od rubnih tačaka kvadratima pripadaju dve stranice i jedan vrh:
. Od rubnih tačaka kvadratima pripadaju dve stranice i jedan vrh:
S druge strane, svake dve od tačaka ![]() ,
, ![]() ,
,
![]() ,
,
![]() , međusobno su udaljene za 1 (u metrici
, međusobno su udaljene za 1 (u metrici ![]() )
pa te tačke moraju imati 4 različite boje. Prema tome,
)
pa te tačke moraju imati 4 različite boje. Prema tome, ![]() .
.
10. Problem popločavanja ravni
Ukrašavanje životnog prostora oduvek je bila ljudska praksa, od velepnih
egipatskih građevina pa do danas. Razvojem i napretkom ljudske kulture
razvija se umetnost i potreba za lepim i skladnim sve više dolazi do izražaja.
Mnogi crteži prikazuju predmete iz života i prirode, a na nekima možemo
uočiti figure koje se periodično ponavljaju, poprimaju geometrijske oblike
sa mnogo simetrije i pokazuju pravilnost kakvu u prirodi retko srećemo.
Tako je vremenom od slobodnih crteža nastao ornament. Stvaralac takvih
crteža morao je sa estetskim ukusom sjediniti i geometrijsko znanje. Javlja
se i potreba za ukrašavanjem zidova i podova. Njih, takođe, možemo ukrasiti
pravilnim geometrijskim figurama.
Problem popločavanja ili parketiranja drevni je problem koji možemo naći
kod starih Egipćana, Persijanaca, Grka, Rimljana, a takođe u Kini, Japanu
i u drugim starim civilizacijama. Šta je to problem parketiranja, tj.
popločavanja ravni? Treba podeliti ravan na mnogouglove koji bi je u potpunosti
prekrivali, bez praznina i preklapanja, uz određene pravilnosti s obzirom
na vrstu, oblik i poredak mnogouglova. Deljenje ravni na pravilne mnogouglove
možemo videti na ulicama, trgovima i na mnogim umetničkim slikama. Time
se pokazuje da matematika i umetnost imaju mnogo toga zajedničkog iako
neki misle da su upravo na suprotnim krajevima širokog i bogatog spektra
ljudskih delatnosti.
11. Pravilna popločavanja ravni
Pre razmatranja problema popločavanja treba uvesti neke osnovne pojmove.
Particija skupa K je familija nepraznih, međusobno disjunktnih podskupova od K kojima je unija čitav skup K.
Zanima nas deljenje ravni na mnogouglove koji imaju zajedničke stranice
i vrhove, a unutrašnjosti su im disjunktne. Takve delove takođe ćemo zvati
particijama. Mnogouglove koji se seku u vrhovima ili stranicama nazivamo
susednim mnogouglovima. Tačku ravni u kojoj se sastaju vrhovi susednih
mnogouglova nazivamo čvorištem particije. Ako su svi uglovi mnogougla
koji se sastaju u jednom čvorištu međusobno jednaki, onda takvo čvorište
nazivamo pravilnim čvorištem. Takođe, kažemo da su dva čvorišta jednaka
ako je broj uglova koji se u njemu sastaju isti. Problem koji se postavlja
jeste pronaći sva moguća deljenja, tj. popločavanja ravni pravilnim mnogouglovima,
pri čemu svi mnogouglovi i sva čvorišta moraju biti jednaki. Takva popločavanja
ćemo zvati pravilnim popločavanjima ravni.
Pokušajmo sada ovaj geometrijski problem zapisati algebarski, tj. svesti
ga na jednačinu. Očito, prvi uslov koji mora biti ispunjen je da zbir
uglova u svakom čvorištu iznosi 360°. Takođe, znamo da zbir unutrašnjih
uglova u n-touglu iznosi (n-2)·180°. Budući da su u pravilnom n-touglu
svi unutrašnji uglovi međusobno jednaki, njihov zbir iznosi
( ( n – 2 ) · 180° ) / n.
Ako se u svakom čvorištu sastaje k pravilnih n-touglova, onda
upravo postavljeni uslov možemo izraziti jednačinom
( k · ( n – 2 ) · 180° ) / n = 360° (1)
uz uslov da su k, n ![]() N i n ≥ 3 (mnogougao sa najmanjim brojem stranica je
trougao). Znači, problem pravilnog popločavanja ravni sveli smo na rešavanje
diofantske jednačine. Rezultat je dat sledećom teoremom.
N i n ≥ 3 (mnogougao sa najmanjim brojem stranica je
trougao). Znači, problem pravilnog popločavanja ravni sveli smo na rešavanje
diofantske jednačine. Rezultat je dat sledećom teoremom.
Teorema: Jedina pravilna popločavanja ravni su na jednakostranične trouglove, kvadrate i pravilne šestouglove, i to tako da ih se u jednom čvorištu sastaje po šest, četiri, odnosno po tri.
Dokaz: Da bismo dokazali ovu teoremu, potrebno je rešiti diofantsku jednačinu (1). Njenim skraćivanjem sa 180 i množenjem sa n dobijemo jednačinu k · ( n – 2 ) = 2n. Dalje, deljenjem sa ( n – 2 ) sledi
k = 2n / ( n – 2 ) = 2 + ( 4 / ( n – 2 ) ). (2)
Rešenja tražimo u skupu prirodnih brojeva pa zaključujemo da ( n – 2
) mora biti delitelj od 4. To znači da je ( n – 2 ) element skupa { -4,
-2, -1, 1, 2, 4 }, odnosno n ![]() { -2, 0, 1, 3, 4, 6 }. Neke mogućnosti možemo odmah eliminisati jer je
n ≥ 3. Ostaju samo tri mogućnosti: n = 3 (jednakostraničan trougao), n
= 4 (kvadrat) i n = 6 (pravilni šestougao). Preostaje nam još da izračunamo
odgovarajuće k-ove, koje dobijemo uvrštavanjem u izraz (2). Tako za n
= 3 dobijamo k = 6, za n = 4 dobijamo k = 4, a za
{ -2, 0, 1, 3, 4, 6 }. Neke mogućnosti možemo odmah eliminisati jer je
n ≥ 3. Ostaju samo tri mogućnosti: n = 3 (jednakostraničan trougao), n
= 4 (kvadrat) i n = 6 (pravilni šestougao). Preostaje nam još da izračunamo
odgovarajuće k-ove, koje dobijemo uvrštavanjem u izraz (2). Tako za n
= 3 dobijamo k = 6, za n = 4 dobijamo k = 4, a za
n = 6 dobijamo k = 3.
Prikažimo pravilna popločavanja ravni!
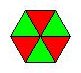

Slika 1.
Popločavanje jednakostraničnim trouglovima vidimo na slici 1. Ovo popločavanje označavamo ( 3, 3, 3, 3, 3, 3 ) - redom napišemo brojeve stranica mnogouglova koji se sastaju u jednom čvorištu. Dakle, imamo šest jednakostraničnih trouglova.


Slika 2.
Na slici 2. vidimo popločavanje kvadratima. Označavamo ga ( 4, 4, 4, 4 ).
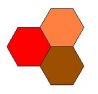
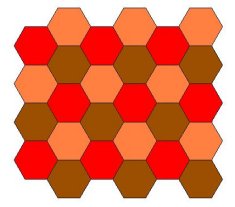
Slika 3.
Konačno, na slici 3. prikazano je popločavanje pravilnim šestouglovima, koje označavamo ( 6, 6, 6 ).
12. Arhimedova popločavanja ravni
Dosad smo proučavali pravilna popločavanja ravni. Razmotrimo sada slučaj kada se u čvorištima sastaje više vrsta pravilnih mnogouglova. Za početak odredimo koliko se najviše različitih pravilnih mnogouglova može sastati u istoj tački. Opet postavljamo isti uslov, da zbir uglova u svakom čvorištu iznosi 360°. Razmatramo jednakostranične trouglove, kvadrate, pravilne petouglove i pravilne šestouglove. Sa αn označimo veličinu unutrašnjeg ugla pravilnog n-tougla. U prethodnom poglavlju koristili smo činjenicu da zbir unutrašnjih uglova u n-touglu iznosi ( n – 2 ) · 180°, iz čega sledi
αn = ( ( n – 2 ) · 180° ) / n. (3)
Postavljeni uslov tada možemo zapisati Σ αn = 360°, gde
se sumira po n = 3, 4, 5, 6. Vrećanjem u formulu (3) vidimo da veličina
unutrašnjeg ugla jednakostraničnog trougla iznosi α3 = 60°, kvadrata α4
= 90°, pravilnog petougla α5 = 108°, a pravilnog šestougla α6 = 120°.
To su pravilni mnogouglovi sa najmanjim brojem stranica i najmanjom veličinom
unutrašnjeg ugla. Pretpostavimo da u nekom deljenju ravni jedno čvorište
čine upravo ta četiri pravilna mnogougla. Tada je 60° + 90° + 108° + 120°
= 378°, što je veće od 360°. Ako bismo zamenili jedan od ovih pravilnih
mnogouglova pravilnim mnogouglom sa većim brojem stranica, odnosno većim
unutrašnjim uglom, suma bi bila još veća. Zaključujemo da kada delimo
ravan na pravilne mnogouglove ne možemo imati više od tri različita pravilna
mnogougla. Time smo dokazali sledeću teoremu.
Teorema: Pri deljenju ravni na pravilne mnogouglove ne možemo imati više od tri različita pravilna mnogougla.
Problem koji se postavlja jeste pronaći sva moguća deljenja, tj. popločavanja ravni u pravilne mnogouglove, pri čemu mnogouglovi mogu imati različit broj stranica, ali sve stranice i sva čvorišta moraju biti jednaki. Takva ćemo popločavanja zvati Arhimedovim ili polupravilnim popločavanjima ravni.
Pokušajmo sada podeliti ravan uz tražene uslove. Za početak uzmimo slučaj deljenja ravni sa dve različite vrste pravilnih mnogouglova. Neka se u jednom čvorištu sastaje k1 pravilnih n1-touglova i k2 pravilnih n2-touglova. Nužan uslov je da zbir uglova oko jednog čvorišta bude 360°, što možemo zapisati jednačinom
k1 · ( ( n1 – 2 ) · 180° ) / n1 + k2 · ( ( n2 – 2 ) · 180° ) / n2 = 360°, (4)
uz uslov da su k1, k2, n1, n2 ![]() N i n1, n2 ≥ 3. Ostaje nam da vidimo da li postoje dodatni
uslovi za k-ove. Znamo da je najmanji broj pravilnih mnogouglova koji
čine jedno čvorište tri (deljenje ravni na pravilne šestouglove) pa zaključujemo
da je k1 + k2 ≥ 3. Takođe, najveći broj pravilnih mnogouglova koji čine
jedno čvorište je šest (deljenje ravni na jednakostranične trouglove)
pa je k1 + k2 < 6 (jer imamo bar jedan mnogougao koji nije trougao).
Rešimo sada jednačinu (4) uz opisane uslove. Skraćivanjem sa 180 i daljim
sređivanjem dobijamo jednačinu
N i n1, n2 ≥ 3. Ostaje nam da vidimo da li postoje dodatni
uslovi za k-ove. Znamo da je najmanji broj pravilnih mnogouglova koji
čine jedno čvorište tri (deljenje ravni na pravilne šestouglove) pa zaključujemo
da je k1 + k2 ≥ 3. Takođe, najveći broj pravilnih mnogouglova koji čine
jedno čvorište je šest (deljenje ravni na jednakostranične trouglove)
pa je k1 + k2 < 6 (jer imamo bar jedan mnogougao koji nije trougao).
Rešimo sada jednačinu (4) uz opisane uslove. Skraćivanjem sa 180 i daljim
sređivanjem dobijamo jednačinu
k1 · ( 1/2 - 1/n1 ) + k2 · ( 1/2 - 1/n2 ) = 1. (5)
Uz uslov 3 ≤ k1 + k2 < 6 za brojeve k1 i k2 imamo sledeće mogućnosti, koje ćemo radi preglednosti zapisati u tablici:
|
1 |
2 |
1 |
3 |
2 |
1 |
4 |
3 |
2 |
k2 |
2 |
1 |
3 |
1 |
2 |
4 |
1 |
2 |
3 |
Za svaku od ovih mogućnosti rešavamo jednačinu (5).
1. slučaj: k1 = 1, k2 = 2 ili k1 = 2, k2 = 1
Uvrstimo vrednosti k1 = 1 i k2 = 2 u jednačinu (5) i sređivanjem dobijamo
n1 = 2 + ( 8 / ( n2 – 4 ) ). (6)
Rešenja za n1 tražimo u skupu prirodnih brojeva pa zaključujemo da (
n2 – 4 ) mora biti delitelj od 8. To znači da je n2 ![]() { -4, 0, 2, 3, 5, 6, 8, 12 }. S obzirom da je n2 ≥ 3, imamo samo pet mogućih
vrednosti za n2. Vraćanjem u (6) dobijamo n1
{ -4, 0, 2, 3, 5, 6, 8, 12 }. S obzirom da je n2 ≥ 3, imamo samo pet mogućih
vrednosti za n2. Vraćanjem u (6) dobijamo n1 ![]() { -6, 10, 6, 4, 3 }. Prva mogućnost ponovo otpada pa imamo četiri mogućnosti
za n1 i n2 ako je k1 = 1 i k2 = 2:
{ -6, 10, 6, 4, 3 }. Prva mogućnost ponovo otpada pa imamo četiri mogućnosti
za n1 i n2 ako je k1 = 1 i k2 = 2:
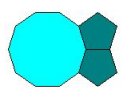
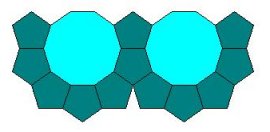
1. n1 = 10, n2 = 5: dva pravilna petougla i pravilni desetougao, ( 5,
5, 10 );
2. n1 = 6, n2 = 6: tri pravilna šestougla, ( 6, 6, 6 );
3. n1 = 4, n2 = 8: kvadrat i dva pravilna osmougla, ( 4, 8, 8 );
4. n1 = 3, n2 = 12: jednakostraničan trougao i dva dvanaestougla, ( 3,
12, 12 ).
Dobijene mogućnosti ne moraju biti rešenja postavljenog problema. Koristili smo nužan uslov da zbir uglova u čvorištu iznosi 360°, koji nije i dovoljan uslov. Sada ćemo pokušati popločati ravan na ta četiri načina.
Slika 4.
1. Krenemo od čvorišta i brojimo stranice mnogougla koji formiraju čvorište, sa tim da počnemo sa mnogouglom koji ima najmanji broj stranica. Uočavamo da ravan ne možemo popločati sa dva pravilna petougla i pravilnim desetouglom jer se pri takvom popločavanju pojavljuje praznina, što nije u skladu sa definicijom popločavanja.
2. Popločavanje ( 6, 6, 6 ) je moguće. To je popločavanje
ravni pravilnim šesterouglovima koje smo videli na slici 3.
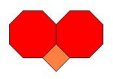
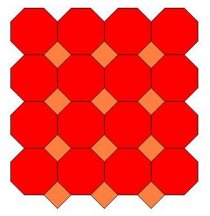
Slika 5.
3. Popločavanje ( 4, 8, 8 ) prikazano je na slici 5. Ravan možemo popločati sa dva pravilna osmougla i kvadratom oko svakog čvorišta bez ikakvih praznina ili preklapanja. Uočimo takođe da su sva čvorišta jednaka, što je u skladu sa definicijom Arhimedovog popločavanja ravni.
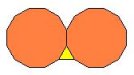
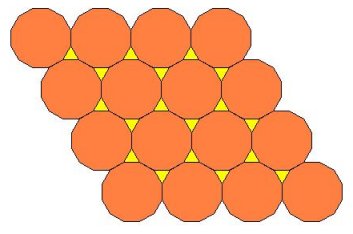
Slika 6.
4. Na slici 6. vidimo da se ravan može popločati na način ( 3, 12, 12 ), tj. tako da se u čvorištima sastaju jednakostraničan trougao i po dva dvanaestougla.
Time smo rešili prvi slučaj. Dobili smo tri rješenja: ( 6, 6, 6 ), (
3, 12, 12 ) i ( 4, 8, 8 ).
Za k1 = 2, k2 = 1 zaključivanje ide potpuno analogno.
2. slučaj: k1 = 1, k2 = 3 ili k1 = 3, k2 = 1
Uvrstimo k1 = 1 i k2 = 3 u jednačinu (5) i sređivanjem dobijamo
n1 = 1 + ( 3 / ( n2 – 3 ) ). (7)
Analognim razmatranjem dobijamo dve mogućnosti za n1 i n2. To su n1 =
n2 = 4 i
n1 = 2, n2 = 6. Drugi slučaj ne zadovoljava uslov n1 ≥ 3 pa za k1 = 1,
k2 = 3 dobijamo samo popločavanje ravni kvadratima prikazano na slici
2.
3. slučaj: k1 = 2, k2 = 2
U ovom slučaju dobijamo dve mogućnosti za n1 i n2 koje zadovoljavaju sve uslove:
1. n1 = 4, n2 = 4: popločavanje ravni kvadratima (slika 2);
2. n1 = 3, n2 = 6 ili obrnuto: u čvorištu se sastaju dva jednakostranična
trougla i
dva pravilna šestougla.
U drugom slučaju trouglove i šestouglove možemo rasporediti na dva načina,
( 3, 6, 3, 6 ) i ( 3, 3, 6, 6 ). Popločavanja su prikazana na slikama
7. i 8. Iako u oba popločavanja nema preklapanja ni praznina, na slici
8. nisu sva čvorišta jednaka pa popločavanje nije Arhimedovo. Dakle, dobili
smo samo jedno novo Arhimedovo popločavanje, prikazano na slici 7.

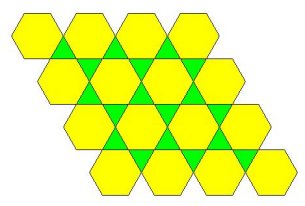
Slika 7.
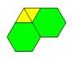
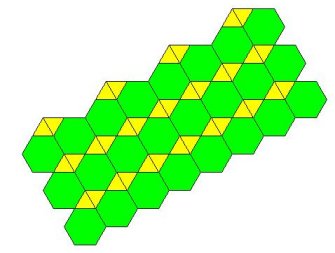
Slika 8.
4. slučaj: k1 = 2, k2 = 3 ili k1 = 3, k2 = 3
Jedino rešenje koje dobijamo u ovom slučaju je popločavanje sa dva kvadrata
i četiri jednakostranična trougla. Tu opet imamo dve mogućnosti: ( 3,
3, 3, 4, 4 ) i ( 3, 3, 4, 3, 4 ).
Odgovarajuća popločavanja prikazana su na slikama 9. i 10. Oba zadovoljavaju
sve uslove Arhimedovog popločavanja ravni.

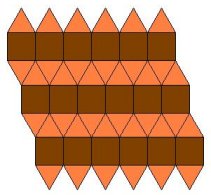
Slika 9.
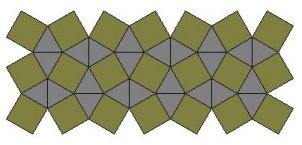
Slika 10.
5. slučaj: k1 = 1, k2 = 4 ili k1 = 4, k2 = 1
U ovom slučaju jedino rešenje je n1 = 6, n2 = 3. Radi se o Arhimedovom popločavanju ravni sa četiri jednakostranična trougla i jednim pravilnim šestouglom (slika 11). Označavamo ga ( 3, 3, 3, 3, 6 ).
![]()

Slika 11.
Ovim smo rešili slučaj popločavanja ravni sa dve različite vrste pravilnih
mnogouglova. Ostaje još slučaj popločavanja ravni sa tri različite vrste
pravilnih mnogouglova. Neka se u jednom čvorištu sastaje k1 pravilnih
n1-touglova, k2 pravilnih n2-touglova i k3 pravilnih n3-touglova. Iz uslova
da zbir uglova oko jednog čvorišta iznosi 360° dobijamo jednačinu
k1 ·(( n1 – 2 )· 180° ) / n1 + k2 ·(( n2 – 2 )· 180° ) / n2 + k3 ·((n3
– 2 )· 180° ) / n3 = 360°,
uz uslove k1, k2, k3, n1, n2, n3 ![]() N, n1, n2, n3 ≥ 3. Analognim zaključivanjem dobijemo
uslov za k-ove koji glasi
N, n1, n2, n3 ≥ 3. Analognim zaključivanjem dobijemo
uslov za k-ove koji glasi
k1 · ( 1/2 - 1/n1 ) + k2 · ( 1/2 - 1/n2 ) + k3 · ( 1/2 - 1/n3 ) = 1. (8)
Imamo tri bitno različita rešenja ove jednačine:
1. k1 = k2 = k3 = 1,
2. k1 = 2, k2 = k3 = 1,
3. k1 = 3, k2 = k3 = 1.
Ako uvrstimo odgovarajuće k-ove u jednačinu (8) dobijamo jednačine, koje rešavamo analogno prethodnim slučajevima. U prvom slučaju dobijamo popločavanje ravni kvadratom, pravilnim šestouglom i pravilnim dvanaestouglom, u oznaci ( 4, 6, 12 ). Prikaz ovog popločavanja dat je na slici 12.
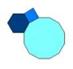
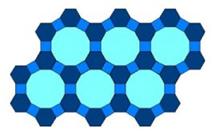
Slika 12.
Rešenje drugog slučaja je popločavanje ravni, sa dva kvadrata, pravilnim
šestouglom i jednakostraničnim trouglom u poretku ( 3, 4, 6, 4 ), (slika
13).

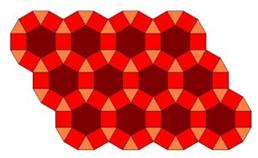
Slika 13.
Ostaje nam da rešimo još slučaj k1 = 3, k2 = k3 = 1. Tražimo deljenje ravni na tri različite vrste pravilnih mnogouglova.
Pretpostavimo da imamo podelu na tri jednakostranična trougla, jedan kvadrat i jedan pravilni petougao. Tada zbir uglova oko jednog čvorišta iznosi 3 · 60° + 90° + 108° = 378°, što je veće od 360°. Jednakostraničan trougao, kvadrat i pravilni petougao su pravilni mnogouglovi sa najmanjom veličinom unutrašnjih uglova. Ako zamenimo bilo koji od ova tri mnogougla nekim drugim, tada će zbir uglova oko čvorišta biti još veći. Zaključujemo da ovaj slučaj nema rešenja.
Sada smo iscrpeli sve mogućnosti. Dobili smo ukupno osam Arhimedovih popločavanja ravni i tako dokazali sledeć teoremu.
Teorema: Postoji ukupno osam Arhimedovih popločavanja ravni.
Zaključak
Ovo je bio pregled najzanimljivijih rezultata u vezi sa starim Nelsonovim
problemom i popločavanjem ravni, ali smo uspeli dotaći i problematiku
nekoliko aktuelnih matematičkih disciplina. Jednostavniji rezultati propratćeni
su dokazima, a za one složenije to bi bilo gotovo neizvodljivo zbog mnogobrojnih
novih koncepata i pojmova.
Ko zna hoće li originalni Nelsonov problem ikada biti rešen?! Poluvekovni
pokušaji njegovog rešavanja ne bi trebalo da deluju obeshrabrujuće. Možda
nam nedostaje samo jedna maštovita dosetka, a možda je ipak "poteškoća"
u aksiomama teorije skupova ili čak temeljima matematičke logike.
Kako god bilo, većina matematičara složiće se da samo rešenje problema
nije uvek najvažnije jer, prema rečima slavnog matematičara i filozofa
Bertranda Russella, matematika ne poseduje samo istinu, već i vrhunsku
lepotu.
Literatura
1. N.G. de Bruijn, P.Erdös, A colour problem for infinite graphs and a problem in the
theory of relations, Nederl. Akad. Wetensch. Indag. Math., 13 (1951) 371-373.2. David Coulson, A 15-colouring of 3-space omitting distance one,
Discrete Mathematics, 256 (2002), 83-90.3. E.D.Demaine, J.S.B.Mitchell, J.O'Rourke, The Open Problems Project,
http://maven.smith.edu/~orourke/TOPP/P57.html#Problem.574. D.Eppstein, The Geometry Junkyard,
http://www.ics.uci.edu/~eppstein/junkyard/open.html5. P.Erdös, On the combinatorial problems which I would most like to see solved,
Combinatorica, 1 (1981), 25-42.6. K.J.Falconer, The realization of distances in measurable subsets covering
,
Journal of Combinatorial Theory, A 31 (1981), 184-189.7. P.Frankl, R.M.Wilson, Intersection theorems with geometric consequences,
Combinatorica, 1 (1981), 357-368.8. M.Gardner, Mathematical Games,
Scientific American, 203 (1960), 180.9. J.E.Goodman, J.O'Rourke (editors), Handbook of Discrete and Computational
Geometry, CRC Press LLC, 1997.10. R.Hochberg, Open Problems for Undergraduates - Graph Theory Open Problems,
http://dimacs.rutgers.edu/~hochberg/undopen/graphtheory/graphtheory.html11. I.Hoffman, A.Soifer, Another six-coloring of the plane,
Discrete Mathematics, 150 (1996), 427-429.12. O.Nechushtan, On the space chromatic number,
Discrete Mathematics, 256 (2002), 499-507.13. E.Pegg, MathPuzzle - The Chromatic Number of the Plane,
http://www.mathpuzzle.com/chrompln.html14. PlanetMath Encyclopedia - Chromatic number of a space,
http://planetmath.org/encyclopedia/ChromaticNumberOfASpace.html15. A.Soifer, A six-coloring of the plane,
Journal of Combinatorial Theory, A 61 (1992), 292-294.16. A.Soifer, Chromatic number of the plane: Its Past and Future,
http://www.math.princeton.edu/~bsudakov/soifer2003.pdf17. S.Shelah, A.Soifer, Axiom of choice and chromatic number of the plane,
Journal of Combinatorial Theory, A 103 (2003), 387-391.
http://www.uccs.edu/~asoifer/18. K.Svozil, The chromatic number of a sphere. Solution of problem nr. 10769,
The American Mathematical Monthly, 108 (2001), 774-775.
http://tph.tuwien.ac.at/~svozil/publ/blatter.html19. L.A.Szekely, Erdös on unit distances and the Szemeredi-Trotter theorems,
http://www.math.sc.edu/~szekely/erdoson1.pdf20. M.Vuković, Matematička logika 1 (skripta), PMF, Zagreb, 2000.
21. Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/Wikipedia
22. D.R.Woodall, Distances Realized by Sets Covering the Plane,
Journal of Combinatorial Theory, A 14 (1973), 187-200.23. S. Bilinski, Problem parketiranja. Matematičko-fizički list 196 (1999), 194-198.
24. V. Galešev, I. Kniewald, L. Kralj, G. Sokol, Informatika 6 - multimedijski priručnik
informatike za 6. razred osnovne škole. SysPrint, Zagreb, 2004.25. I. Kniewald, Logo 4.0. Alfej, Zagreb, 1999.
I. Kniewald, Terrapin Logo. SysPrint, Zagreb, 2005.26. A.N. Kolmogorov, Parketi iz pravilnih mnogouglova. Matematika i škola 10 (2001).
27. K. Krulić, Popločavanja ravnine i njihova primjena u nastavi matematike u osnovnoj i
srednjoj školi. Diplomski rad, Sveučilište u Zagrebu, 2005.28. L.F. Toth, Reguläre Figuren. Akademiai Kiado, Budapest, 1965.
29. S. Sruk, Simetrično je lepo. Matematika i škola 10 (2001), 213-216.
30. E.W. Weisstein, Regular Tessellation.
http://mathworld.wolfram.com/RegularTessellation.html31. E.W. Weisstein, Tessellation. http://mathworld.wolfram.com/Tessellation.html
preuzmi
seminarski rad u wordu » » »
