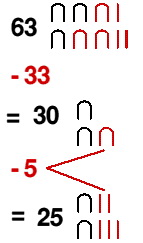OSTALI SEMINARSKI RADOVI
IZ MATEMATIKE: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
RAČUNANJE STARIH EGIPĆANA
‘’Pošto nama priliči da ispitamo početke I umetnosti I nauka sa stanovišta sadašnjeg vaseljenskog ciklusa,kažimo da je ,prema svim izvorima,geometrija prvo otkrivena među Egipćanima,I da vodi poreklo od merenja zemljišta. Jer, oni su je smatrali neophodnom zbog podizanja nivoa Nila koji bi zbrisao svačije međe. Niti ima ičeg iznenađujućeg u tome što otkriće ove I drugih nauka potiče iz praktične potrebe,jer sve što je u procesu nastajanja napreduje od nesavršenog ka savršenom,tako da je prirodan prelaz od opažanja do zaključivanja I od zaključivanja do razumevanja. Upravo kao što tačno poznavanje brojeva vodi poreklo od Feničana zbog trgovine I ugovaranja,tako je geometrija otkrivena među Egipćanima iz navedenog razloga.’’ — Proklo
Prema Proklovim rečima geometrija je ponikla u Egiptu iz praktične potrebe da se posle izlivanja Nila poplavljeno zemljište premeri I ponovo parceliše. Ovaj podatak može se naći u Herodotovoj Istoriji I Proklo ga je odatle svakako I preuzeo. Herodot kazuje da
‘’Svaki kome bi reka odnela nešto zemlje morao je to odmah da javi kralju. Tada bi ovaj poslao svoje činovnike da pregledaju I izmere za koliko se zemlja smanjila I da prema tome odrede koliku će porezu ubuduće plaćati. Izgleda mi da je u vezi s tim pronađena I geometrija I da je odatle kasnije dospela u Heladu.’’ [Istorija,II.109]
I Aristotel je delio ovo mišljenje o poreklu geometrije. U Metafizici [981b], govoreći o znanjima koja su se pojavila u zemljama u kojima su ljudi imali slobodnog vremena na pretek,on tvrdi da je:
„Egipat bio kolevka matematičke nauke jer je tu svešteničkom staležu bilo ostavljeno mnogo slobodnog vremena.“
Demokrit je za sebe umeo da kaže:
„U konstruisanju linija pri iznošenju dokaza nije me niko pretekao ,čak ni takozvani harpedonapti (zatezači konopa) u Egiptu.“[23,vol.II,str.187]
Ko su mogli biti harpedonapti koje pominje Demokrit?
Oni su bili ili pripadnici svešteničkog staleža iz Aristotelove tvrdnje, ili činovnici koji su premeravali zemljište koristeći se najjednostavnijim sredstvima u koje je svakako spadao I konop koji su zatezali. Po tome su dobili svoje grčko ime harpedonapti-zatezači konopa. Njima je prepuštano da pre početka gradnje hramova ili grobnica orijentišu građevinu i odrede njenu osnovu. Prilikom izgradnje piramida ovo nikako nije moglo biti jednostavno imajući u vidu njihove dimenzije. Ali,veština harpedonapta bila je impresivna. To se najbolje vidi iz podatka da se odstupanje osnove velike piramide u Gizi od besprekornog kvadrata čija je ivica oko 230 metara,meri santimetrima.
Iz dvaju dokumenata pisanih na papirusu od kojih je jedan poznat po imenu Rajndov papirus,koji je nastao oko 1750.godine stare ere,a drugi je Moskovski koji je stariji stotinak godina,saznajemo koje matematičke istine su bile poznate činovnicima i sveštenicima starog Egipta. U njima je sačuvano mnoštvo rešenih matematičkih problema,delom iz aritmetike,a delom iz geometrije. Dvadeset četvrti problem Rajndovog papirusa glasi [67,str.5][31,str154]:
„Gomila-njena sedmina ,njeno celo ,to je 19.“
Mi bismo rekli: Odrediti nepoznatu veličinu ako je zbir njene sedmine i nje same jednak 19. Lako ćemo sastaviti jednačinu
1/7x + x = 19,
I utvrditi da je njeno rešenje 165/8. I Ahmes,pisac Rajndovog papirusa, dobija isto rešenje. Razume se,on ne sastavlja jednačinu već samo opisuje računski postupak kojim se dolazi do tog rešenja. U osnovi ovog postupka koji će kasnije dobiti ime „metoda lažnog rešenja“,krije se dobro poznavanje proporcije. Ako treba rešiti linearnu jednačinu
ƒ (x) = C,
pretpostavićemo da je x1 „lažno rešenje“ ove jednačine. Možemo očekivati da je tada ƒ (x1) ≠C pa ,ako je
ƒ (x1) = C1,
iz proporcije
x : x1 = C : C1
nalazimo tačno rešenje u obliku
x = x1C/C1.
Za Ahmesa, kao uostalom i za svu egipatsku matematiku, svaki problem je pojedinačni problem za koji se propisuje procedura rešenja. Nema opštih razmatranja i nema dokazivanja.
O staroegipatskoj matematici doznajemo ponajviše iz dvaju čuvenih papirusa: Ahmesovog ili Rhindovog (desno) i Moskovskog (levo). Rhindov papirus je 1858. otkrio škotski egiptolog Henry Rhind u Luxoru. To je zapravo svitak dužine 6 m, širine 30 cm. Pisao ga je pisar Ahmes oko 1650 g. pr. Hrista i verovatno je nastao tako što je Ahmes prepisivao neki spis star 200 godina. Danas se čuva u British Museumu u Londonu, a sadrži 87 matematičkih problema. To je jedna kompletna "studija o svim stvarima, pogled u unutrašnjost svega što postoji, saznanje o tamnim tajnama", kako piše u samom papirusu. Ahmesov papirus je zbirka tablica i vežbi, retorička u svojoj formi, koja je namenjena uglavnom učenju matematike. Sadrži vežbe iz aritmetike, algebre, geometrije i raznih merenja. Moskovski papirus otkrio je 1893. godine V. S. Golenichev. Dug je 6 m, širok 8 cm. Sadrži 25 problema, od kojih mnogi nisu čitljivi. Čuva se u Moskovskom muzeju.
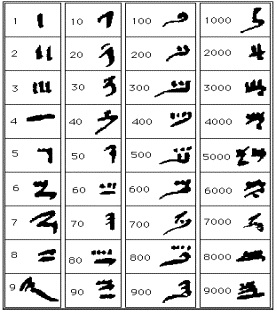
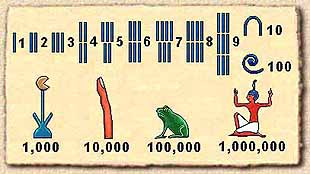
Stari Egipćani imali su razvijen decimalni sistem i svoje oznake za brojeve:
Hijeroglifskim znacima se pisalo po kamenu kako s leva na desno, tako i obrnuto, a ponekad i odozgo prema dole. Različito pisanje ne stvara probleme kod čitanja bojeva jer egipatski način pisanja brojeva nije pozicijski. Hijeratički su znaci uvedeni za brzo pisanje po papirusu, drvu ili po lončariji.
Osim navedenih, upotrebljavali su se povremeno i neki posebni znakovi za brojeve koji nisu dekadne jedinice. Npr. za broj dva crtali bi se goveđi rogovi, za broj pet morska zvezda, a ljudska glava bila je i oznaka za broj sedam (7 otvora).
Na poseban su način označavali razlomke, tako specifičan da nema sličnosti ni s jednom drugom kulturom. Razlomak čiji je brojilac jedan zapisivao se tako da se iznad znaka za imenilac stavio poseban znak sa značenjem "deo". Svi razlomci pisali su se s jediničnim brojiocem, a ako to nije bilo moguće, onda su ga prikazivali kao zbir takvih.Evo nekoliko primera zapisa nekih brojeva:
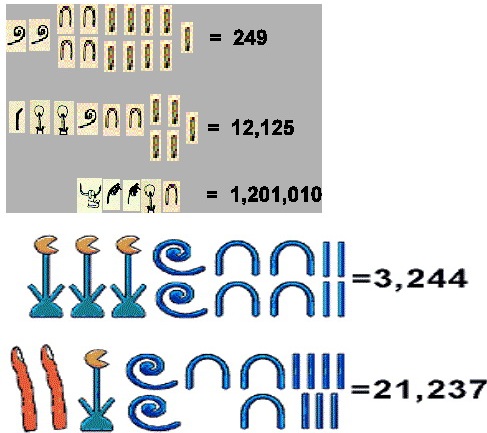
Koristili su brojevni sistem s bazom 10, a jedna od glavnih razlika između hijeratičkih brojeva i našeg brojevnog sistema jeste da hijeratički brojevi nisu bili pisani u sistemu mesnih vrednosti, tako da su cifre mogle biti pisane bilo kojim redosledom. Hijeratički je sistem adicijski sistem. Vidimo da se, recimo, broj 249 zapisuje kao 249 = 2 100 + 4 10 + 9, pa u zapisu imaju dva znaka za 100, četiri znaka za 10 i devet znakova za 1.
Kako su racunali stari Egipćani?
Egipatski brojevni sistem nije bio pogodan za računanje, ali je trgovina zahtevala sabiranje, oduzimanje, množenje, deljenje te rad s razlomcima. Sabirati je bilo najlakše!
Sabiralo se skupljanjem istih simbola zajedno i pretvaranjem njih 10 u jedan simbol sledećeg nivoa:
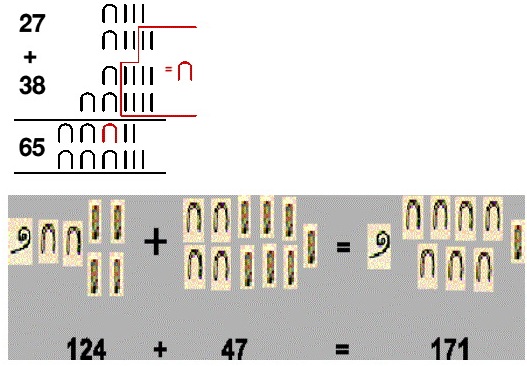
Oduzimalo se tako da se odmicao određeni broj istih simbola. Ovo je znalo biti i komplikovano kad se moralo oduzeti više simbola nego što ih je bilo prisutno u prikazu. Npr. evo kako bi izračunali 63-38.
Od 6 desetica možemo oduzeti 3 desetice, ali možemo ukloniti samo 3 jedinice. Još nam preostaje 5 jedinica za oduzimanje. Jedna od preostalih desetica potrebna je da se omogući oduzimanje sledećih 5 jedinica jer
1 desetica – 5 jedinica = 10 jedinica – 5 jedinica = 5 jedinica.
Tačan mehanizam oduzimanja koji su koristili nije sasvim jasan, iako ova ilustracija pokazuje kojim je redosledom pisar mogao sprovesti oduzimanje.
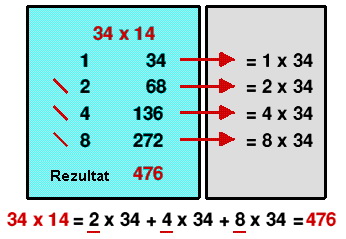
Množenje prirodnih brojeva odaje nam da su se služili i potencijama broja 2. Stari Egipćani množili su dva broja koristeći udvostručavanje brojeva.
U plavom pravougaoniku prikazan je njihov zapis, a sivi pravougaonik i račun ispod pravougaonika objašnjava metodu.
Broj su udvostručavali sabirajući ga samog sa sobom, dakle, samo su zapisali brojeve jedan ispod drugog i pretvorili svakih 10 istih simbola u simbol sledećeg nivoa.
Kako nisu imali razvijen pozicijski zapis brojeva, moramo starim Egipćanima priznati veliku spretnost i ekonomičnost u računanju.Kao što se vidi u tablici hijeroglifskih znakova, egipatski brojevni sistem koristio je simbole koji predstavljaju potencije broja 10 s eksponentima od 0 do 6. I oni su uočili da je množenje broja s 10 jednostavno: zamenili bi svaki simbol onim susednim po veličini, npr.
236 10 = (6 jedinica postaje 6 desetica, 3 desetice postaju 3 stotice, 2 stotice postaju 2 hiljade) = 2 hiljade, 3 stotice i 6 desetica = 2360.Evo jednog od poslednjih problema Rhindovog papirusa: "Na imanju je sedam zgrada. U svakoj od njih je sedam mačaka. Svaka od mačaka uhvati po sedam miševa, a svaki od njih pojede po sedam zrna pšenice. Svako bi zrno moglo dati sedam merica žita. Koliko je na imanju ukupno zgrada, mačaka, miševa, zrna pšenice i merica žita?"
Rešenje u našim oznakama dato je s:
zgrada 7
mačaka 49
miševa 343
zrna 2401
merica 16807
-----------------------
19607
Deljenje kod starih Egipćana zahtevalo je korištenje množenja i vrlo često upotrebu razlomaka. Pogledajmo prvo primer deljenja kad je rezultat ceo broj:
-125 podijeljeno s 5 daje isti rezultat kao 5 pomnoženo s ??? = 125
-množi 5 uzastopno s višekratnicima od 2 sve dok ne dobiješ 125 (kao kod množenja)
-zbir crveno označenih brojeva u plavom pravougaoniku daje rešenje.
Ova metoda temelji se na jednostavnoj matematičkoj činjenici koja je bila poznata i egipatskim pisarima,a to je da su množenje i deljenje inverzne operacije,tj.
a b = c ako i samo ako je c : b = a.
Kad je pisar morao računati s razlomcima, bio je suočen s mnogim problemima, uglavnom vezanim za njihovo zapisivanje. Njihove metode zapisivanja nisu im dopuštale da pišu jednostavne razlomke kao što su 3/5 ili 15/33 zato što su svi razlomci morali biti prikazani s brojiocem 1. Ako to nije bilo moguće, onda se razlomak morao zapisati kao zbir razlomaka s brojiocem 1. Izuzetak u tome je bio razlomak 2/3. Razlomci su zapisivani tako da je iznad imenioca stavljen hijeroglif koji je označavao "otvorena usta" . Danas pojednostavljeno razlomke s jedinicom u brojiocu pišemo s kosom crtom iza koje sledi imenilac, npr. 1/2 zapisujemo kao /2, 1/4 kao /4, dok se izuzetak, 2/3, piše //3.
Postojala su i određena pravila pri računanju s razlomcima:
• kad se razlomak može prikazati na više načina, koristi se način koji zahteva najmanji broj jediničnih razlomaka,
• uvek se koristi najveći mogući jedinični razlomak, osim ako to nije u kontradikciji s prvim pravilom,
• u prikazu razlomka 2/n ne mogu se koristiti dva ista jedinična razlomka,
• jedinični razlomci pišu se od većeg prema manjem.
Primeri koji objašnjavaju ova pravila:
1. Razlomak 3/4 pisar je mogao zapisati kao /2 /4, ili /3 /4 /6. Uvek se koristi kraća verzija.
2. Razlomak 7/12 mogao se zapisati kao /2 /12, ili /3 /4. Pisar bi koristio /2 /12 jer mora koristiti veći jedinični razlomak, /2 koji je veći od /3.
3. Razlomak 9/10 nije se mogao zapisati kao /2 /5 /5 zato što se jedinični razlomak može koristiti samo jednom u prikazu. Zato bi se 9/10 pisao kao //3 /5 /30.
4. Zadnji primer pokazuje kako su razlomci u zbiru pisani u padajućem redosledu: //3 > /5 > /30.
1/3 3/4 = 1/2 + 1/4
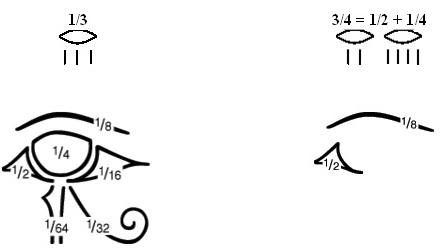
Stari Egipćani verovali su da ih "Rx" simbol, tj. simbol boga Horusa štiti od zla. Zato su i u matematiku ugradili simboliku pa su razvili i svojevrstan brojevni sistem koji se koristio za prepisivanje lekova, podelu zemlje ili semenja. Razlomke su pravili tako što su kombinovali pojedine delove simbola oka boga Horusa. Svaki deo imao je različitu vrednost. Celokupni simbol oka ima vrednost 1, a celi sistem se temelji na podeli na polovine. Pola od 1 je 1/2, pola pola od 1/2 je 1/4, itd. sve do 1/64. .
Npr., da bismo prikazali razlomak 5/8, kombinujemo razlomke 1/8 i 1/2.Važnost 2/3 kao jedinog razlomka koji nisu rastavljali na jedinične i koji su vrlo mnogo koristili u računima, pronalazimo u tome što su stari Egipćani znali i koristili činjenicu da se 2/3 od 1/n može računati kao 2/3 1/n = 1/(2n) + 1/(6n). Kako su bili vešti u računanju, a pogotovo zato što nigde nisu pronađeni neki pomoćni računi. Veruje se da su imali dobro i precizno razrađene tablice rastava razlomaka, sabiranja i oduzimanja osnovnih i sl., koje su im omogućavale brzo i efikasno računanje s razlomcima.
Stari Egipćani su imali razvijenu geometriju, stereometriju i sve ono što im je bilo potrebno za izgradnju piramida i hramova. Znamo da su znali računati nagib piramide, zapreminu zarubljene piramide te zapreminu piramide. Računali su površinu trougla kao 1/2 umnoška dve kraće stranice (što vredi samo za pravougli trougao); mala odstupanja nisu im značila previše. Znali su izračunati i površinu pravougaonika kao umnožak dužina njegovih stranica.
Deo Moskovskog papirusa
o izračunavanju zapremine
zarubljene piramide
Ono što je fascinantno, a pronađeno je u Ahmesovom papirusu, je kako su računali površinu kruga:
• pretpostavimo da krug ima prečnik od 9 kheta (khet je jedinica za dužinu),
• uzmi 1/9 prečnika, dakle 1,
• ostatak je 8,
• pomnoži 8 sa 8,
• dobiješ 64 i to je površina!
Kad bismo to zapisali savremenim matematičkim jezikom, P = (8/9 x prečnik)2, i uporedili rezultat s egzaktnom formulom za izračunavanje površine kruga, P = r2π, dobili bismo zanimljiv rezultat: stari Egipćani su gotovo 1000 godina pre stvarnog otkrića broja π znali njegovu približnu vrednost. Naime, po njihovim računima π bi iznosio približno 3.1605!
Formula slična egipatskoj za površinu kruga dobija se upoređivanjem kruga s kvadratom:
• prečnik kruga je 9, dakle, opiše mu se kvadrat stranice dužine 9
• podeli svaku stranicu kvadrata na trećine
• formirati osmougao kao na slici
• površina dobijenog osmougla približno je jednaka površini kruga
• površina osmougla jednaka je površini kvadrata umanjena za dva mala kvadrata sačinjena od 4 "odrezana" trougla2
P(osmougla) = 9 9 – 4(1/2 3 3) = 63 64 = 8
Staroegipatska algebra bila je retorička, problemi i rešenja dati su rečima. Znali su rešavati jednačine prvog stepena s tim da su obavezno sprovodili analizu i sintezu pri rešavanju, tj. svako rešenje su uvrštavali u početni problem da se uvere da to jeste pravo rešenje.
Stari Egipćani nisu poznavali oznake za množenje, deljenje, jednakost, kvadratni koren, decimalnu tačku, nisu čak ni znali za "obični" razlomak p/q, nisu se pitali zašto nešto funkcioniše, nisu tražili univerzalnu istinu formulisanu simbolima koji bi jasno i logički pokazali njihov misaoni proces. Ali su se zato koristili i sedmocifrenim brojevima, imali su neku čudnu mešavinu jednostavnosti i komplikovanosti u svojim računima, ali taj se koncept pokazuje kao potpuno jedinstvena i zatvorena celina.
Zato se može reći da je egipatska matematika jedini sačuvani čisti primerak računske tehnike koja je bila vrlo razvijena, koja u čitavom svom razvoju nije doživela nikakav bitni diskontinuitet, već se u potpunosti temelji na osnovi računanja - na brojenju i pojmu razlomka.
Na jednom zidu hrama u Edfu ostao je sačuvan način izračunavanja površine trapezoida I to množenjem poluzbirova suprotnih stranica. Formula nije tačna,ali greška je minimalna.
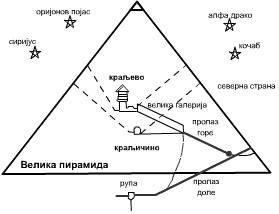
Egipćani su poznavali transcedentni broj π (odnos obima I prečnika kruga) tj.kvadrat stranice a=16,ima istu površinu kao i krug poluprečnika r=9, što bi prema današnjim formulama mogli napisati: : r2π= a2, odakle sledi egipatski "π" = (16/9)2, koji približno iznosi 3,16 a to je minimalna greška.Egipćani nas najviše fasciniraju gradnjom Velike piramide i njenom geometrijom, kao i hramovima. Savršeno orjentisanih prema stranama sveta ,dva miliona kamenih blokova teških do 54 tone,čine Veliku piramidu u Gizi,s takvom preciznošću da su uglovi pravi tačni do jedan posto,a stranice dužine 230 metara u dužini se razlikuju minimalno.
Najzanimljiviji i po proporcijama najsuptilniji egipatski hram Velika piramida je skiciran ispod. Donje isprekidane linije su hodnici koji kreću iz Kraljevske komore (na slici,levi ka Sirijusu). Oni sa stranicama piramide formiraju pravougle trouglove. Kateta, hipotenuza i njihov zbir, desnog od trouglova odgovara trima uzastopnim članovima Fibonačijevog niza. Uzastopni članovi Fibonačijevog niza se koriste za izračunavanje zlatnog preseka,naročitog estetskog odnosa u građevinarstvu. To nije slučajno, jer je i u drugim hramovima(naročito u Karnaku) vođeno računa o „zlatnim proporcijama“. Osim toga i dimenzije Kraljevske sobe su u Fibonačijevom nizu.
Površina trougla:
Metod izračunavanja površine trougla koji su Egipćani koristili ekvivalentan je današnjoj formuli P = ½ b*h, gde je b – osnovica, a h – visina trougla. Jedina nejasnoća kod ovog metoda je ta što se ne zna pouzdano da li su Egipćani stvarno uzimali visinu trougla, ili su uzimali drugu njegovu stranicu, što ne daje tačno rešenje, osim u slučaju pravouglog trougla.Površina kruga:
U starim egipatskim matematičkim spisima možemo naći više primera izračunavanja površine kruga. Autor daje sledeća uputstva:
• od prečnika se oduzme njegova jedna devetina
• ono što ostane, diže se na kvadrat.Problem 50 iz Rindovog papirusa:
izračunati površinu kruga čiji je prečnik 9 jedinica dužine. Kada se oduzme njegova jedna devetina, dobija se 8. 8 pomnoženo sa 8 (kvadrirano) daje 64. Uopšteno bi izgledalo ovako:
P = (8/9d)²
Ovo rešenje je veoma blizu onom koje dobijamo današnjom metodom:
P = (d/2)²π = 63.617
Iz ove dve jednačine se može izvući vrednost broja π, do koje su došli stari Egipćani, iako ga nisu posebno imenovali:
(8/9d)² = (d/2)²π
64/81d² = ¼ d²π
64*4/81 = π
256/81 = π
π ≈ 3.1605Površina geometrijskih tela:
Površina ravnih geometrijskih tela računala se , kao što se to i danas radi, sabiranjem površina pojedinačnih stranica. Kod zaobljenih tela se već javljaju manji problemi. U starim skriptama postoji samo nekoliko zadataka koji se bave ovom problematikom, ali se naučnici još nisu složili oko prevoda hijeroglifa. Tačnije, ne zna se pouzdano o kom telu se govori: polucilindru, polulopti ili čak polukrugu, a rezultati su takvi da približno odgovaraju svakom slučaju.
Zapremina valjka:
Zapremina valjka računala se na isti način kao danas. Prvo bi se našla površina baze, a zatim ona pomnožila visinom valjka. Postupak izračunavanja površine baze opisan je u delu gde je prikazan način računanja površine kruga. Jedina komplikacija kod ovih zadataka bila je u prevođenju jedinica zapremine, u kojima se dobijao rezultat, u one koje su se koristile u svakodnevnom životu. U nekim primerima mere su prevođene tek kad se zapremina izračunala, a u nekim se to činilo odmah na početku, što je komplikovalo račun uvođenjem razlomaka tj. odnosa tih mernih jedinica.
Zapremina piramide:
Stari papirusi i kamene table ne mogu nam mnogo reći o tome koliko su stari Egipćani znali o geometrijskim osobinama prave piramide, iako najvredniji deo zaostavštine starog egipatskog carstva predstavljaju grobnice baš u tom obliku. Sve što sigurno znamo je da su mogli da izračunaju nagib, površinu i zapreminu prave i zarubljene piramide kvadratne osnove
Nagib su računali na sledeći način: date su visina i dužina osnove piramide. Dužina osnove se podeli sa 2, a zatim i sa visinom. Dobijeni rezultat označavao je dužinu za koju se osnova produži kada se visina poveća za jednu jediničnu dužinu. Može se reći da je to ustvari kotangens nagiba strane piramide. Rezultat se, po potrebi, izražavao u različitim mernim jedinicama. U Rhindovom i Moskovskom papirusu možemo naći više problema ovog tipa, samo različito formulisanih u zavisnosti od toga koje veličine su date, a koje se traže.
Poznato nam je da su stari Egipćani znali formulu za izračunavanje zapremine prave piramide (V = 1/3 h a²), ali nema podataka o tome kako su do nje došli. Najlakše je bilo napraviti šupalj kvadar i piramidu istih osnova i visina, i uporediti količine vode ili peska koje u nju staju. Iako nije nigde zabeleženo, smatra se da su znali kako da izračunaju zapreminu kvadra i to baš formulom V = a*b*c (dužina*širina*visina), tako da je zapremina odgovarajuće piramide iznosila V = 1/3 h a². Takođe su se figure mogle napraviti od rečnog mulja i izmeriti, da bi se dobio odnos njihovog masa, a samim tim i zapremina. Ne tako jednostavna jeste metoda isecanja piramide na manje delove i njihovog kombinovanja do tela oblika kvadra, čija se zapremina lako računa.
U svakom slučaju, mnogo komplikovanije je bilo izvođenje formule za zapreminu zarubljene piramide, jer se do nje pre došlo matematičkim putem, nego ispitivanjem odnosa zapremina tela u praksi.
Jedini zadatak koji se bavi zapreminom piramide je problem 14 iz Moskovskog matematičkog papirusa. Ovde je, bez sumnje, određen standardni metod izračunavanja zapremine zarubljene piramide, što predstavlja vrhunac dostignuća ove oblasti staroegipatske matematike.
Problem 14 iz Moskovskog papirusa:
Dato je:
• visina 6
• dužina donje osnovice 4
• dužina gornje osnovice 2
Postupak je:
• Kvadrirati 4. Rezultat 16.
• Udvostručiti 4. Rezultat 8.
• Kvadrirati 2. Rezultat 4.
• Na 16 dodati 8, a zatim i 4. Rezultat 28.
• Izračunati 1/3 od 6. Rezultat 2.
• To pomnožiti sa 28. Rezultat 56.
To bismo danas zapisali ovako:
V = (4*4 + 4*2 + 2*2) * 1/3 * 6 = 56
Kada brojeve zamenimo opštim oznakama za veličine, dobijamo opštu formulu za izračunavanje zapremine zarubljene piramide:
V = (a*a + a*b + b*b) * 1/3 * h = h/3 (a² + ab + b²)
Smatra se da se do ove formule stiglo metematičkim putem: zapremina zarubljene piramide dobija se oduzimanjem zapremine male piramide, odsečene od vrha, od zapremine cele piramide.
Egipatski kalendar:
Izuzetno matematičko znanje stari Egipćani su pokazali i u računanju vremena. Njihova organizacija kalendara održala se do danas i predstavlja uopšte najveće naučno dostignuće u ovoj oblasti.
Egipatski kalendar sastojao se od 12 meseci od po 30 dana (36 dekada od po 10 dana) i 5 „završnih“ dana posvećenih bogovima Ozirisu, Horusu, Setu, Izisu i Neftusu. Ovi poslednji dani bili su rođendani pomenutih bogova, 12 meseci bilo je podeljeno na 3 godišnja doba od po 4 meseca:
• period poplava tj. setve,
• period rasta,
• letnji period tj. period žetve.
Ovakav način računanja vremena održao se baš zato što tako organizovana godina nigde nema prekida u toku tj. približno je tačno izračunat period trajanja jedne godine posle kog se ciklus godišnjih doba ponavlja. Kasnije su ga koristili i stari Heleni, a zatim i sam Kopernik i drugi astronomi srednjeg veka.
Danas se zna da solarna godina traje 365 ¼ dana, pa se zato svake četvrte godine dodaje po jedan dan. Tako je utvrđena prestupna godina. I stari Egipćani su znali za ovo, ali nisu uveli prestupnu godinu. Tako bi svake četiri solarne godine standardna računska godina za solarnom kasnila jedan dan, svakih 120 godina za 30 dana tj. jedan mesec, svakih 1440 godina za 12 meseci tj. jednu godinu. Iako ne u velikoj meri, to se primećivalo u toku životnog veka. Međutim, Egipćane to i nije tako brinulo kao neki drugi problemi svakodnevnog života. Oni jednostavno nisu poklanjali puno pažnje pomeranju godišjih doba u odnosu na računsku godinu, dok su izuzetno poštovali solarnu.
Značaj naučnog dostignuća starih Egipćana u računanju vremena leži u uporedom postojanju ova dva kalendara – kalendara računske godine i kalendara solarne godine. Iako je vreme računato po standardnoj računskoj godini, ona je bila sporedna stvar u svakodnevnom životu. Sve privredne aktivnosti bile su planirane po solarnoj godini. Solarna godina se još naziva i Sirijusova godina, po Sirijusu, najsjajnijoj zvezdi na nebu. Sirijus se na nebu pojavljivao nešto pre izlaska Sunca u vreme kada je Nil nadolazio i kada su počinjale poplave. Tada su Egipćani započinjali setvu i planirali dalje izvođenje poljoprivrednih aktivnosti.
Egipatski kalendar nam svedoči, ne samo o matematičkim dostignućima, nego i o izuzetnom poznavanju astronomije, iako tada još nisu postojali složeni instrumenti za posmatranje nebeskih tela.
Zaključak
Stari Egipćani su jedan od prvih naroda koji je, radi praktične primene, počeo da razvija matematiku, i na taj način, nesvesno, joj otvorio vrata budućnosti.
Nekada je bilo potrebno mnogo vremena da bi se došlo do nekog saznanja, sada elementarnog za nas. Danas se izuzetno složene i duge operacije zamenjuju mnogo bržim i lakšim, a to je sve moguće zahvaljujući drevnim civilizacijama, koje su se prve uputile stazom naučnog spoznavanja naše stvarnosti. Matematika starih civilizacija, među kojima je i egipatska, dala je osnove za dalji razvoj ove nauke. Iako komplikovana, ponekad i nespretna, ona nosi pečat originalnih misli i stremljenja, i svojom baštinom nas zadužuje da otkrivamo, upoznajemo i definišemo novo, da uvek proširujemo granice poznatog.
Literatura:
1. Zoran Lučić „Ogledi iz istorije antičke geometrije“
2. Miloš Radojčić „Opšta matematika“-Naučna knjiga, Beograd,1950.
3. www.math.e.hr
4. www.wikipedia.org
5. www.math.buffalo.edu
preuzmi
seminarski rad u wordu » » »