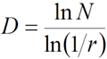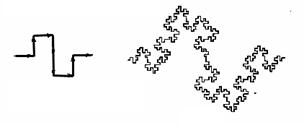Reč fraktal skovao je Benoit Mandelbrot 1975.od latinskog prideva fractus, što znači razlomljen,slomljen,nepovezan. Teško je dati preciznu definiciju fraktala i fraktalne geometrije. Čak je i sam Mandelbrot (kojeg bismo mogli nazvati ocem fraktalne geometrije,iako su neki takvi objekti bili poznati i puno ranije) bio neodlučan pred tim problemom,pa je za svoju definiciju fraktala,koju je bio ponudio,rekao da izuzima neke objekte koji bi se trebalo zvati fraktali. Ta definicija glasila je: fraktal je skup za koji je Hausdorff-Besicović dimenzija veća od topološke dimenzije. Definicija koja bi bila nešto bolja i preciznija je ona da je fraktal objekt koji ima necelobrojnu fraktalnu (Hausdorff-Besicović) dimenziju. Pre svega,treba naglasiti da je dimenzija jedan od onih entiteta kojima pridajemo intuitivno značenje,kao što su vreme, prostor, masa itd.,zato da bi dali preciznu definiciju fraktalnog objekta,treba prvo precizno definisati dimenziju.
Topološka dimenzija je najbliža intuitivnom ,prirodnom shvatanju: tačka ima topološku dimenziju 0, prava 1, ravan 2, a prostor 3. Precizna definicija glasi: Skup ima topološku dimenziju 0,ako svaka tačka ima proizvoljno malu okolinu čiji rub ne seče skup.
Fraktalna dimenzija je vrednost koja nam daje uvid u to u kojoj meri neki fraktal ispunjava prostor u kojem se nalazi. Postoji mnogo definicija fraktalne dimenzije i ni jedna se ne može smatrati univerzalnom. Fraktalnu dimenziju je najbolje objasniti na primeru Cantor-ovog skupa.

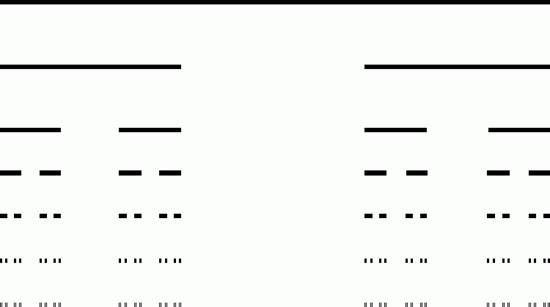
Cantorov skup

Taj jednostavni fraktal izum je George Cantor-a ,nemačkog matematičara, osnivača teorije skupova,koji ga je proučavao još 1872. Kako je sa slike očigledno, nastaje primenom jednostavnog algoritma: uzmemo jediničnu pravu,zatim posmatramo skup tačaka na toj pravoj Sk=[0,1], izbacimo tačke intervala [1/3,2/3] iz skupa Sk, potom istu operaciju primenimo na preostala dva odvojena dela prave tj. izbacimo tačke intervala [1/9,2/9] i [7/9,8/9] i tako dalje. Očigledno je da svaka iteracija odreže 1/3 skupa koji je ostao od prethodne iteracije. Dužina skupa u n-toj iteraciji ja tada (2/3)n , ako je početna dužina jedinična,međutim,svejedno i kada n→∞,skup ima beskonačno mnogo elemenata.
Fraktali su geometrijski objekti čija je fraktalna dimenzija strogo veća od topološke dimenzije. Drugim rečima,to su objekti koji daju jednaki nivo detalja bez obzira na broj iteracija koji koristimo tj. količinu razdeljivosti. Dakle, fraktale je moguće uvećavati beskonačno mnogo ,a da se pri svakom novom uvećanju vide neki detalji koji pre uvećanja nisu bili vidljivi i da količina novih detalja uvek bude otprilike jednaka. Oni su (barem približno) samoslični tj. sastoje se od umanjenih verzija samih sebe,ali i suviše nepravilni da bi se opisali jednostavnom geometrijom. Laički rečeno,oni su "načičkani" do u beskonačnost. Fraktalne slike nastaju iteracijom – upornim uzastopnim ponavljanjem nekog računskog ili geometrijskog postupka.
Fraktali su, dakle, slike nastale ponovljenim matematičkim računom ili geometrijskom konstrukcijom
Osnove
Jedne od najjednostavnijih i najpoznatijih fraktalnih krivih su Kochova kriva i Kochova pahuljica,koje je predstavio švedski matematičar Niels Fabian Helge von Koch (1870.-1924.) 1904.godine.Razlika izmedju krive i pahuljice je u tome što se kod konstrukcije krive počinje sa pravom,a kod pahuljice sa jednakostraničnim trouglom. Topološka dimenzija im je 1,a fraktalna

Krećemo od prave (nulta iteracija) koju podelimo na 3 jednaka segmenta,zatim na srednji segment dodamo još dve prave jednakih dužina (1/3 dužine prvobitne dužine), tako da zajedno sa srednjim segmentom prave jednakostranični trougao. Nakon toga uklonimo srednji segment.Sada imamo 4 prave jednakih dužina i to nazivamo prvom iteracijom.Drugu iteraciju dobijamo tako što svaku od četiri prave prve iteracije zamenimo umanjenom verzijom cele prve iteracije.Kochovom krivom nazivamo geometrijski lik koji nastane kad broj iteracija teži nuli.Skup tačaka početne prave koji ostane "na kraju" jednak je Cantorovom skupu.

Kochova kriva → konstrukcija

Kochova kriva, prva iteracija

Kochova kriva, druga iteracija

Kochova kriva, treća iteracija

Kochova pahuljica se stvara na isti način kao Kochova kriva,ali tako što se uzmu tri početne prave i stave tako da obrazuju jednakostranični trougao. Sa svakom od prava učinimo isto što i sa nultom iteracijom Kochove krive da bi smo dobili prvu iteraciju.

Kochova pahuljica → konstrukcija:

Kochova pahuljica, nulta iteracija

Kochova pahuljica, prva iteracija

Kochova pahuljica, druga iteracija
Kochova pahuljica-druga iteracija
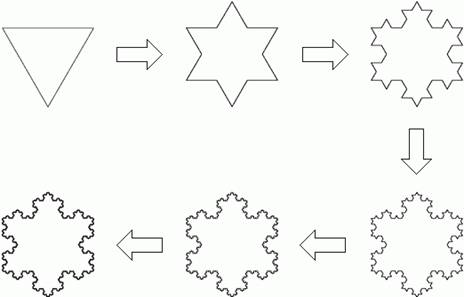
-stvaranje Kochove pahuljice-

Još jedan od poznatih fraktala je trougao Sierpińskog, koji je opisao poljski matematičar Wacław Franciszek Sierpiński 1915. godine. Njegova fraktalna dimenzija je .

Nulta i prve četiri iteracije trougla Sierpińskog

Da bi konstruisali trougao Sierpińskog, počinjemo od jednakostraničnog trougla(nulta iteracija) koji se zameni trima trouglovima upola manje dužine stranice(prva iteracija). Zatim se postupak ponovi sa svakim trouglom (druga iteracija) i tako u beskonačnost.

Podela

Postoje razni načini klasifikacije fraktala.Jedan od načina je svrstati ih po stupnju samosličnosti.Potpuno samoslični fraktali su oni koji sadrže kopije sebe koje su slične celom fraktalu.Primeri ove grupe su svi geometrijski fraktali kao što su trougao Sierpińskog, Kochova kriva, Hilbertova kriva, Cantorov skup itd. Ako fraktal sadrži male kopije sebe koje nisu slične celom fraktalu,nego se pojavljuju u iskrivljenom obliku,govorimo o kvazi samosličnom fraktalu. To su Mandelbrotov i Julijin skup i sl. Moguće je i da fraktal ne sadrži kopije samog sebe,ali da neke njegove osobine (npr. fraktalna dimenzija) ostaju iste pri različitim procenama. u tom slučaju govorimo o statističkoj samosličnosti,a tipičan primer je Perlinov šum.
Fraktale je moguće klasifikovati i po načinu njihovog nastanka.Sistemi iteriranih funkcija nastaju korišćenjem homotetije,translacije ili rotacije kopije i mogućim zamenjivanjem nekog elementa kopijom. Fraktali definisani rekurzivnim relacijama određeni su rekurzivnom formulom koja određuje da li određena tačka prostora(npr. kompleksne ravni) pripada skupu ili ne. Slučajni fraktali nastaju crtanjem grafova nekih stohastičkih procesa npr. Brownovog gibanja.Zanimljivo je da i prva i druga podela daje isti rezultat- sistemi iteriranih funkcija daju potpuno samoslične fraktale,fraktali definisani rekurzivnim relacijama su kvazi samoslični,a slučajni fraktali su statistički samoslični.Zbog jednostavnosti,za te tri skupine se koriste nazivi geometrijski, algebarski i stohastični fraktali. Ta podela izgleda ovako:

1.geometrijski fraktali

na pravi - Cantorov skup
u ravni - Cantorova prašina, Kochova kriva, trougao Sierpińskog, tepih Sierpińskog, Apolonijeva mreža, beskonačno guste krive: Peanova kriva, Hilbertova kriva, kriva Sierpińskog, zmajolika kriva
u trodimenzionalnom prostoru - Oktaedarski fraktal, Dodekaedarski fraktal, Ikosaedarski fraktal, zatim analogoni nižedimenzionalnim fraktalima: Cantorov oblak, Kochova površina, tetraedar Sierpińskog

2.algebarski fraktali
Julijin skup, Mandelbrotov skup, goreći brod

3.stohastični fraktali
bifurkacijski dijagram, Lorenzov atraktor, Brownovo gibanje i Brownovo drvo, Perlinov šum

Primena

Najčešća primena fraktala je u računarskoj grafici. Najjednostavniji primer je stvaranje terena,posebno planina. Planina se stvara tako što se horizontalno položenom trouglu svaki vrh povisi ili snizi za slučajno odabranu vrednost. Tada se dobijenom trouglu spajaju polovine stranica,te se tako dobijaju četiri nova trougla. Srednjem od njih (omeđenom trima pravama koje spajaju polovine stranica prvobitnog trougla) povisimo ili snizimo vrhove kao i početnom trouglu,ali koristimo dvostruko manje vrednosti. Postupak se onda ponavlja za sva četiri trougla. Planine se mogu napraviti i na drugi način, pomoću Perlinovog šuma.

Planina stvorena koristeći Perlinov šum Rastinje stvoreno pomoću fraktala

Pomoću sistema iteriranih funkcija u tri dimenzije moguće je kreirati raznoliko rastinje - grmove,drveće,busene trave i sl. Rezultati mogu biti zapanjujuće slični stvarnim pojavama u prirodi.
Fraktali se koriste i u kompresiji podataka.Od manje važnih primena tu je (naravno,veoma ograničeno) predviđanje nekih stohastičkih procesa kao što su potresi; slaganje snopova optičkih vlakana, oponašanje rada neuronskih mreža za razvoj veštačke inteligencije itd. Za male uređaje,kao što su mobilni telefoni,proizvode se antene u obliku fraktala koje,zbog toga,mogu koristiti širok spektar frekvencija ne zauzimajući mnogo mesta.
Model za vojnu kamuflažnu odeću koristi fraktalnu strukturu koja se nigde ne ponavlja,te se stoga mnogo teže primećuje u prirodi,gde ništa nije matematički pravilno. Rade se istraživanja za lečenje aritmije srca,gde srce kuca u haotičnom režimu. Spoljnom stimulacijom srca pokušava da se postigne prelaz u pravilan režim. Na kraju,neke fraktalne strukture su izrazito lepe,pa se prezentuju kao umetnička dela.

Fraktali u prirodi

Kristalizirani med daje fraktalnu strukturu Fraktalna struktura brokule

Mogućnost primene fraktala leži u činjenici da su mnogi od njih slični prirodnim pojavama.Često se kao primer koristi posebna vrsta brokule i paprat. Med kristalizira u fraktalne oblike ,a drveće je,kao i paprat,po svojoj prirodi fraktalnih svojstava (deblo se grana na grane koje se granaju na grančice...). Zapravo,na neki način,ceo svet je sačinjen od fraktalnih oblika. Mandelbrot je koristio primer obale mora kao fraktal. Svi fraktalni postupci se mogu nastaviti sve do molekulskih razmera. Mnogo je delova ljudskog tela fraktalne strukture. Očigledan primer je sistem krvnih žila,koje u principu imaju istu strukturu kao i drveće. DNK se vezuje dajući fraktalnu strukturu. Primeri su nebrojani.

L-sistem

L-sistem ili Lindenmayerov sistem je formalna gramatika koja je najpoznatija po primeni u modeliranju rasta procesa razvoja biljaka, ali i za modeliranje morfologije raznih organizama. L-sistemi se mogu koristiti za generisanje samosličnih fraktala kao što su sistemi iteriranih funkcija. L-sistem je uveo i razvio 1968. mađarski teoretski biolog i botaničar sa Univerziteta u Utrechtu, Aristid Lindenmayer (1925.–1989.).

Struktura L-sistema

Rekurzivna priroda L-sistema vodi ka samosličnosti i stoga fraktalnim oblicima koji se lako opisuju L-sistemom. Modeli biljaka i izgledom prirodnih organskih oblika se slično lako definišu, a kako se dubina rekuzije povećava, oblik polako 'raste' i postaje složeniji. Lindemayerovi sistemi su takođe popularni u generisanju veštačkog života.
Gramatike L-sistema su vrlo slične semi-Thue gramatici. L-sistemi su danas uobičajeno poznati kao parametarski L sistemi definisani n-torkom:

G = {V, S, ω, P},
gde je

V (abeceda) - skup simbola koji sadrže elemente koji mogu biti zamenjeni (varijable)
S - skup simbola koji sadrže elemente koji ostaju fiksirani (konstante)
ω (početak, aksiom ili inicijator) - niz simbola iz V koji definišu inicijalno stanje sistema
P - skup pravila produkcija ili produkcija koje definišu način na koji varijable mogu biti zamenjene konstantama i drugim varijablama. Produkcija se sastoji od dva stringa - prethodnika i sledbenika.

Primer 1: Fibonaccijevi brojevi

Ako definišemo sledeću jednostavnu gramatiku: varijable : A B
konstante : nijedna
početak : A
pravila : (A → B), (B → AB)

tada ovaj L-sistem generiše sledeći raspored stringova:
n = 0 : A
n = 1 : B
n = 2 : AB
n = 3 : BAB
n = 4 : ABBAB
n = 5 : BABABBAB
n = 6 : ABBABBABABBAB
n = 7 : BABABBABABBABBABABBAB
Ovo su slike u ogledalu stringova prvog primera, sa zamenjenim A i B. Još jednom, svaki je string nadovezivanje prethodna dva, ali u obrnutom redosledu.
U bilo kojem od primera, ako izračunamo dužinu svakog stringa, dobijemo poznati Fionaccijev niz brojeva:
1 1 2 3 5 8 13 21 34 55 89 ...
Za n>0, ako brojimo k-tu poziciju od invarijantnog kraja stringa, vrednost je određena time pripada li stepen zlatnog preseka unutar intervala (k-1,k). Razmer A i B stoga konvergira ka zlatnom preseku. Ovaj primer daje isti rezultat (u terminima dužine svakog od stringova, ne u nizovima simbola A i B) ukoliko je pravilo (B → AB) zamenjeno pravilom (B → BA).

Primer 3: Cantorov skup

varijable : A B
konstante : nijedna
početak : A {početni znak stringa}
pravila : (A → ABA), (B → BBB)
Neka A znači "crtaj napred" i B znači "pomakni napred".
Ovo generiše poznatov Cantorov fraktalni skup za realnu pravu u R.

Primer 3: Kochova kriva

Varijanta Kochove krive koja koristi samo prave uglove.
varijable : F
konstante : + −
početak : F
pravila : (F → F+F−F−F+F)
Ovde, F znači "crtaj napred", + znači "zarotiraj ulevo za 90°", i - znači "zarotiraj udesno za 90°"
n = 0:
F
n = 1:
F+F-F-F+F
n = 2: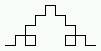
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F
n = 3:
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+ F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F- F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F- F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+ F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

Primer 4: Fraktalna biljka

varijable : X F
konstante : + −
početak : X
pravila : (X → F-X+X]+F[+FX]-X),(F → FF)
ugao : 25º
Ovde, F znači "nacrtaj napred", - znači "zarotiraj ulevo za 25º" i + znači "zarotiraj udesno za 25º". X ne odgovara nijednoj akciji crtanja i koristi se za upravljanje evolucijom krive. [ odgovara spremanju trenutnih vrednosti za poziciju i ugao, koje se vraćaju izvršavanjem odgovarajućeg ].

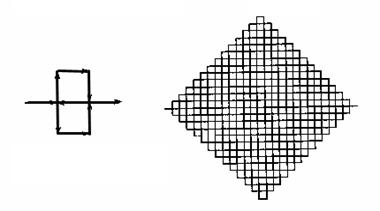
Zmajolika kriva

Zmajolika kriva (en. Dragon curve) je beskonačno gusta kriva koja je dobila ime po mitološkom biću kojem je slično. Ponekad se to ime koristi za sve fraktalne krive koje se mogu konstruisati rekurzivnim metodama kao što je Lindenmayerov sistem.

Konstrukcija → najčešće se crta pomoću L-sistema

ugao: 90 º
početak: FX
pravila:

X $\mapsto$ X + Y F +
Y $\mapsto$ - F X - Y

značenje:

F = "crtaj napred"
- = "zarotiraj u smeru kazaljke na satu za 90 º "
+ = "zarotiraj u smjeru suprotnom od smera kazaljke na satu za 90 º "

prva iteracija: F X + Y F +
druga iteracija: F X + Y F + + - F X - Y F +
treća iteracija: F X + Y F + + - F X - Y F + + - F X + Y F + - - F X - Y F +
četvrta iteracija: F X + Y F + + - F X - Y F + + - F X + Y F + - - F X - Y F + + - F X + Y F + + - F X - Y F + - - F X + Y F + - - F X - Y F +

Osim toga, moguće ju je prikazati i kao sistem rekurzivnih funkcija u kompleksnoj ravni:
$f_1(z)=\frac{(1+i)z}{2}$ , $f_2(z)=1-\frac{(1-i)z}{2}$
Uprkos čudnom obliku, zmajolika kriva ima relativno jednostavne dimenzije:

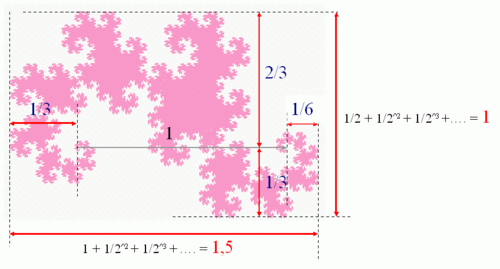
Površina se jednostavno može videti iz njenog popločanja: površina slike gore je pola kvadratne jedinice.
Samosličnost je jasno vidljiva: svaki "deo" je manji za $\sqrt{2}$ i rotiran za 45˚.

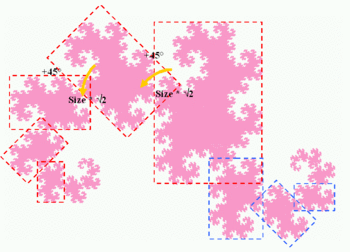
Fraktalna dimenzija joj je, kao i svim beskonačno gustim krivama u ravni 2, a fraktalna dimenzija njene granice se procenjuje na 1.5238.

Perlinov šum

Perlinov šum je vrsta matematičke funkcije koja se koristi na nebrojene načine u računarskoj grafici. Funkcija se dobija sabiranjem više funkcija koje su dobijene slučajnim odabiranjem tačaka, gde svaka sledeća funkcija ima dvostruko manju amplitudu i dvostruko veću frekvenciju. Osmislio ju je Ken Perlin 1983. godine.

Konstrukcija

Postupak ćemo objasniti na primeru jednodimenzionalne funkcije. Prvu funkciju konstruišemo tako da na određenom segmentu apscise odredimo pet jednako udaljenih tačaka i pripišemo im slučajno izabrane vrednosti intervala [-128,128], zatim interpoliramo ostale tačke odabranim postupkom, u ovom slučaju kosinusnom interpolacijom:

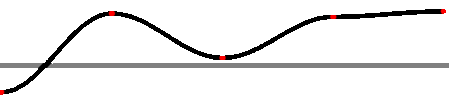
Drugu funkciju konstruišemo na isti način, samo što odabiramo devet tačaka (uključujući i pet iz prošle funkcije) i pripisujemo im slučajne vrednosti u intervalu [-64, 64]. Sad imamo (približno) dvostruko više tačaka, a amplituda je dvostruko manja:

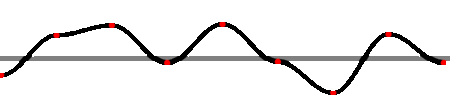
Nastavljamo na isti način, sa 17 tačaka intervala [-32 i 32]:

33 tačke, vrednosti u intervalu [-16, 16]:

65 tačaka, intervala [-8, 8] (ovde tačke nisu naglašene jer ih je previše):

Na kraju jednostavno saberemo sve te funkcije dobijajući planinoliku strukturu zvanu Perlinov šum u intervalu [-120, 120]:

Svojstva
Perlinov šum je funkcija spojena od više funkcija od kojih svaka ima "izbočine" i "udubine". One su otprilike jednakih dimenzija na pojedinoj funkciji, ali se njihove dimenzije razlikuju kad se te funkcije upoređuju. Time skup tih funkcija daje strukturu koja ima velike "izbočine" i "udubine", na kojima postoje manje, a koje opet sadrže još manje, i tako unedogled. To je temeljni razlog zbog kojeg Perlinov šum toliko podseća na planinu - planine takođe imaju neki osnovni oblik, ali i taj osnovni oblik ima svoje udubine i izbočine, koje nisu ravne...Potrebno je napomenuti da Perlinov šum nije jedna određena funkcija, nego se svaki put dobije drugačiji rezultat. To je posledica uzimanja slučajnih vrednosti za tačke. Perlinov šum spada u kvazi-samoslične fraktale. To je stoga što se uvećavanjem slike uvek dobija još veći nivo detalja,ali ipak nijedan deo slike nije sličan (u matematičkom smislu) celini. Naravno, ovde govorimo o "savršenom" Perlinovu šumu, koji bi bio skup beskonačno mnogo funkcija (od kojih bi zadnja imala beskonačno malenu amplitudu i beskonačno mnogo odabranih tačaka). U praksi se broj iteracija (funkcija koje se sabiraju) određuje po potrebi. Fraktalna dimenzija ovisi o algoritmu kojim je funkcija pravljena (npr. o vrsti interpolacije).
Primena
Perlinov šum se pretežno upotrebljava u računarskoj grafici. Najjednostavnija primena je stvaranje grafičkih krajolika. Radi se o jednostavnom "crtanju" dvodimenzionalne funkcije u trodimenzionalnom koordinatnom sistemu. Spektar primena još se više proširuje jednostavnim "dorađivanjem" funkcije Perlinova šuma. Ako uzmemo apsolutne vrednosti Perlinovog šuma i rezultat prikažemo u tonovima narandzaste boje, rezultat će ličiti na vatru. Dodamo li toj funkciji funkciju f(x) = sinx te malo promenimo boje, dobićemo teksturu koja liči teksturi obrađenog mermera.Različitim matematičkim i grafičkim postupcima možemo postići najrazličitije teksture.

Kako se određuje dimenzija fraktala?

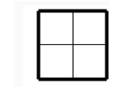
	1 dimenzija: N pravih, svaka je dužine r: Nr1=1
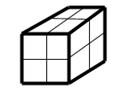
	2 dimenzije: N kvadrata, svaki je površine r2: Nr2=1
	3 dimenzije: N kocaka, svaka je zapremine r3: Nr3=1
Fraktalna dimenzija se opšte može definisati kao:
gde je

Evo nekoliko primera kako se računa fraktalna dimenzija:

	Jedinična prava razdeljena je na 3 jednake manje prave. Svaka je dugačka 1/3 jednične prave,pa je r=1/3, N=4, a dimenzija ovog fraktala: D=ln(4)/ln(3)=1.26
	Jedinična prava razdeljena je na 4 jednake manje prave. Svaka je dugačka 1/4 jednične prave, pa je r=1/4, N=8,a dimenzija ovog fraktala: D=ln(8)/ln(4)=1.5
	Jedinična prava razdeljena je na 3 jednake prave (r=1/3) i svaka se zamjenjuje uzorkom od 9 manjih pravih: N=9. Dimenzija ovog fraktala je: D=ln(9)/ln(3)=2 Kod ovog fraktala, za razliku od prethodna dva, kada 1/r teži beskonačnosti fraktal potpuno prekriva ravan, D=2.

LITERATURA:

WWW.WIKIPEDIA.ORG
WWW.ESKOLA.HFD.HR
WWW.MATHOS.HR
WWW.INET.HR

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi