OSTALI SEMINARSKI RADOVI
- INFORMACIONI SISTEMI - |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
Digitalni potpis
1. Uvod- Općenito o digitalnom potpisu
Današnji opće prihvaćeni način ovjeravanja dokumenata vlastoručnim potpisom vuče korijene od samih početaka ljudske pismenosti. Potpisi se danas nalaze na najrazličitijm dokumentima, od različitih ugovora, naloga, čekova pa sve do privatnih pisama. Prema postojećim zakonima potpisom se smatra ne samo vlastoručni potpis, već i bilo koji drugi znak na dokumentu načinjen s ciljem ovjeravanja dokumenta. Ipak, na računalima se ne smatra svaki potpis digitalnim potpisom. Različite znakovne ili tekstualne oznake u datotekama ili elektronskoj pošti ili kopije vlastoručnog potpisa krajnje su neprimjerene i nepouzdane, prije svega zbog trivijalnog krivotvorenja. Razvojem i širenjem računala a napose računalnih mreža, postalo je jasno da je potreban posve novi način ovjeravanja. Temelji za pouzdanu provjeru porijekla informacija, «digitalni potpis», stvoreni su 1976. godine otkrićem kriptografije javnog ključa (Diffie-Hellman), koja se još naziva i asimetričnom kriptografijom. Zanimljivo je napomenuti da je ovaj način kriptiranja podataka, prema nekim informacijama bio poznat britanskoj tajnoj službi nekoliko godina prije nego spomenutoj dvojici istraživača.
Danas, kada većina razvijenih zemalja u svoje zakone uvodi i zakon o digitalnom potpisu, ovo područje se nalazi na granici dva svijeta, kriptografije i prava. Osim pravnih problema oko primjene digitalnog potpisa, postoje i pravni problemi vezani uz implementaciju algoritama digitalnog potpisa, uglavnom zbog softverskih patenata kojima je velik broj algoritama zaštićen, ali i zbog restriktivnih regulativa pojedinih zemalja vezanih uz kriptografske proizvode općenito. Tako je npr. izvoz «jakog» enkripcijskog softvera iz SAD-a bio zabranjen sve do pred kraj 1999. godine. Isto tako, u Francuskoj je upotreba alata za enkripciju bila zabranjena do početka 1999. Ipak, naglim širenjem elektronskog poslovanja postalo je nužno ovakve odredbe ukinuti, i omogućiti kako sigurnu zaštitu informacija šifriranjem tako i zaštitu od mogućih prijevara, autentifikacijom. Upravo idealnim za ovo potonje nameće se digitalni potpis.
2.1. Osnovni principi rada digitalnog potpisa
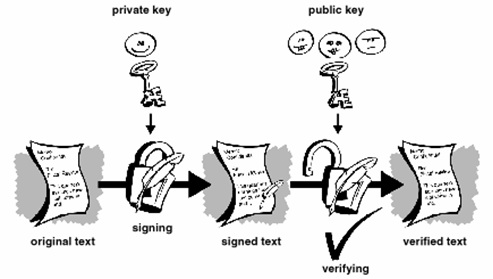
Slika 1. Princip digitalnog potpisaPretpostavimo da dvoje ljudi Luka i Petar, žele razmjenjivati potpisane poruke (podatke) tj. žele biti sigurni u identitet osobe od koje su poruku dobili. Kao prvo, obje osobe kreiraju par komplementarnih ključeva, javni i tajni ključ. Važno je naglasiti da se poznavanjem javnog ključa ne može izračunati tajni ključ u nekom razumnom vremenu (vrijeme potrebno za izračunavanje tajnog ključa iz poznatog javnog ključa, tj. razbijanje šifre, mjeri se milijunima godina na danas najjačim raspoloživim računalima). Nakon kreiranja ključeva, Luka i Petar razmjenjuju svoje javne ključeve, a potom Luka, koristi svoj tajni ključ za šifriranje sažetka poruke koji je izračunao nekom od «Hash» funkcija. Hash funkcija je funkcija koja iz zadane poruke (podataka) računa sažetak fiksne duljine. Kada Petar uspije dešifrirati sažetak poruke javnim ključem od Luke, on još računa i sažetak primljene poruke koji potom uspoređuje s upravo dešifriranim, i ako je izračunati sažetak jednak onom dešifriranom, primatelj može biti siguran u porijeklo poruke (podataka), jer je poruka mogla biti šifrirana jedino Lukinim tajnim ključem, kao i u integritet poruke.
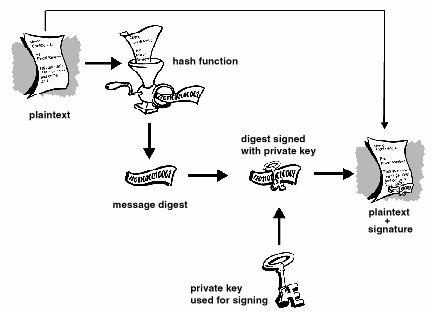
Slika 2. Princip potpisivanja poruke
U cijeloj proceduri samo je jedna stvar slaba karika. Moramo biti apsolutno sigurni da javni ključ za koji mislimo da pripada Luki zaista i pripada njemu. Naime, ukoliko Petar ima javni ključ od neke treće osobe, a vjeruje da ključ pripada pošiljatelju Luki, tad je ta treća osoba u mogućnosti krivotvoriti Lukine podatke .2.2. Uloga povjerljive stranke
Opisani problem rješava se na način da se uvodi «povjerljiva stranka». Pretpostavka je da povjerljivoj stranci sve ostale stranke vjeruju, te da svoje javne ključeve osobno odnesu na potpisivanje, s tim da im PS prethodno provjeri uobičajene «fizičke» dokumente. U tom slučaju PS koristi svoj tajni ključ za potpisivanje javnog ključa te time garantira svima ostalima ispravnost potpisanog javnog ključa.
Postoji i druga mogućnost, a to je da PS svima generira par ključeva, te uz prethodnu fizičku autentifikaciju, dodjeljuje ključeve. U tom slučaju svatko tko bi htio provjeriti ispravnost potpisa neke osobe morao bi u bazi javnih ključeva (koju čuva PS) pronaći javni ključ te osobe i potom tim ključem pokušati dešifrirati primljene podatke. Nedostatak ovog drugog modela je taj što u tom slučaju PS posjeduje i tajne ključeve što predstavlja znatan sigurnosni problem ako se isti par ključeva koristi osim za potpisivanje i za šifriranje podataka.
3. Potpisi i zakoni
Zakonske regulative (zemalja koje imaju zakon o digitalnom potpisu) ne određuju niti jednu tehnologiju potpisivanja kao dominantnu, već samo donose propise kojih se svaka od tehnologija mora pridržavati. Kao prvo, od digitalnog se potpisa očekuje da bude jedinstven osobi koja ga koristi, drugo, da se može provjeriti kome pripada odnosno da li zaista pripada osobi koja ga je koristila, treće, da je u potpunoj kontroli osobe koja ga koristi, četvrto, da potvrđuje i sebe i podatke koje potpisuje.
Već iz ovog vidimo da postoji znatna prednost digitalnog potpisa nad klasičnim metodama autentifikacije. Najveća prednost je ta što se valjanost potpisa provjerava svaki put pri primitku dokumenta, za razliku od klasičnih potpisa koji se provjeravaju tek na sudu, kad se prijevara već odigrala. Osim ove prednosti postoji još jedna značajna prednost, a to je nemogućnost naknadne izmjene potpisanog dokumenta, kao i nemogućnost potpisivanja praznih dokumenata. Ipak, ukoliko krivotvoritelj uspije doći do tajnog ključa, tada bez ikakvih problema može falsificirati podatke bez da postoji i najmanja mogućnost utvrđivanja različitosti takvog potpisa od pravog potpisa, što kod klasičnih metoda ipak nije slučaj.
Nemali broj kriptografskih algoritama zaštićen je različitim patentima. Tako je npr. najrašireniji asimetrični kriptografski algoritam, RSA, bio patentiran 17 godina sve do rujna 2000. godine, a drugom isto tako vrlo značajnom protokolu, Diffie-Hellman protokolu, patent je istekao u travnju 1997. godine. Nažalost, ovo nisu jedini takvi primjeri kao ni jedini problemi u široj primjeni kriptografskih algoritama. Proizvođači kriptografskog softvera (bili) su prisiljeni proizvoditi po dvije ili čak tri različite verzije istog softverskog paketa da bi se udovoljilo svim izvoznim i patentnim regulativama; zabrana izvoza kriptografskog softvera iz SAD-a s ključem dužim od 40-bita bila je na snazi do pred kraj 1999. godine, tako da je npr. NAI («Network Associates») bio prisiljen imati dvije verzije svog programa PGP, jednu za tržište SAD-a a drugu za internacionalnu tržište. Ipak, obje su verzije koristile «jaku» enkripciju tako što je iskorištena «rupa» u zakonu SAD-a kojim se zabranjuje izvoz softvera u binarnom obliku ali ne i izvornog koda na papiru. Osim ovog, postojao je i problem zbog patentiranog RSA algoritma, tako da verzije za SAD nisu koristile istu inačicu kao i internacionalne.
Sličan problem javlja se i s pojavom novog američkog standarda za digitalno potpisivivanje («Digital Signature Standard», DSS, 1994), jer se dijelovi korištenog algoritma (koji sam po sebi nije patentiran) nalaze pod patentnom zaštitom autora sličnog algoritma temeljenog na diskretnim logaritmima. Ovaj primjer ipak odskače iz mnoštva drugih upravo zbog toga što se radi o standardu koji su obavezne koristiti sve državne ustanove SAD-a; drugim riječima ovaj će patent vrlo vjerojatno američki porezni obveznici osjetiti na vlastitom džepu.
Na kraju spomenimo još i zabranu izvoza bilo kakvog kriptografskog softvera zemljama poput Iraka, Sjeverne Koreje ili Kube.4. Kriptografski temelji digitalnog potpisa
Današnje tehnike digitalnog potpisivanja temelje se na algoritmima asimetrične kriptografije, poznate još i pod nazivom kriptografija javnog ključa (engl. «public key cryptography»). Algoritme javnog ključa (engl. «public-key algotithms») možemo podijeliti u tri osnovne grupe:
1. algoritmi temeljeni na praktičnoj nemogućnosti faktoriziranja velikih prim brojeva (RSA)
2. algoritmi temeljeni na praktičnoj nemogućnosti izračunavanja diskretnih logaritama (Diffie-Hellman protokol, DSA)
3. algoritmi temeljeni na eliptičnim krivuljama (praktične realizacije ove metode su tek u povojima)
Osim ovih algoritama postoji još i nekolicina rjeđe korištenih, temeljenih na praktičnoj nemogućnosti utvrđivanja sadržaja ruksaka (engl. «knapsack algorithms», Merkle), no većina današnjih komercijalnih implementacija se može svrstati u jednu od tri glavne kategorije. Recimo još i to da se različite verzije Knapsack algoritma ne smatraju sigurnima zbog toga jer su Rivest i Shamir (neovisno jedan o drugom, Rivest prvu verziju, Shamir dorađenu nakon prvotnog uspješnog razbijanja) uspjeli «razbiti» ovakvu zaštitu.
5. a) Korištenje RSATipičan algoritam iz prve skupine je i najčešće korišteni algoritam javnog ključa, RSA. Algoritam započinje na sljedeći način. Izaberimo dva velika prim broja p i q. Nakon toga izračunamo n=p*q i z=(p-1)*(q-1). U slijdećem koraku uzimamo broj relativno prost broju z i nazivamo ga d. Još nam je jedino potreban e takav da vrijedi e*d=1 mod z. Kad smo izračunali sve ove parametre, spremni smo za šifriranje podataka. Prije svega potrebno je poruku P podijeliti u dijelove od kojih svaki sadrži najviše n znakova (obično se zbog toga uzimaju blokovi po k bitova tako da vrijedi 2k = n). Da bismo šifrirali poruku računamo C=Pe (mod n) a za dešifriranje je potrebno izračunati P=Cd (mod n). Za šifriranje RSA algoritmom potrebni su dakle e i n, a za dešifriranje d i n. Iz toga vidimo da se javni ključ sastoji od (e,n) a tajni ključ od (d,n). Sigurnost ove metode sadržana je u tome što je vrlo teško faktorizirati velike prim brojeve. Teoretski postupak izračunavanja RSA algoritma krajnje je jednostavan. Naime, faktoriziranjem n dobijemo p i q. Iz p i q vrlo jednostavno izračunamo z. Uz poznati z i e (koji je dio javnog ključa) Euklidovim algoritmom dolazimo do d i imamo i tajni ključ (d,n). Ipak, da bi se faktorizirao 200-znamenkasti prim broj potrebno je oko 4 milijarde godina, uz korištenje najboljeg mogućeg algoritma i računala s vremenom izvođenja instrukcije od 1 sec.
5. b) Korištenje DSA“Digital Signature Algorithm” se koristi za potpisivanje kao i za provjeru valjanosti već načinjenog potpisa. Svaki potpisnik posjeduje javni i tajni ključ. Tajni ključ se koristi u procesu stvaranja digitalnog potpisa, a javni ključ se koristi u procesu provjere valjanosti potpisa. U oba slučaja se algoritam primjenjuje na sažetak poruke, M, načinjen korištenjem “Secure Hash Algorithm” funkcije. Bez poznavanja tajnog ključa potpisnika nije moguće stvoriti valjan potpis, tj. nije moguće krivotvoriti potpis (u razumnom vremenskom periodu). Unatoč tome, svatko je u mogućnosti provjeriti valjanost potpisa korištenjem javnog ključa potpisnika.
Prije korištenja DSA mora se utvrditi nekakva povezanost para ključeva (javnog i tajnog) sa korisnikom. To se obično ostvaruje već opisanim potpisivanjem javnog ključa od strane “povjerljive stranke” (engl. “trusted party”) uz prethodnu provjeru stvarnih fizičkih dokumenata.
Slika 3. Uspješni završetak dogovora o digitalnom potpisu
Zaključak
Budućnost digitalnog potpisa je u svakom slučaju svijetla. Koja god tehnologija ili algoritam bili korišteni, teško je već danas zamisliti svijet računalnih mreža bez odgovarajućih algoritama autentifikacije. No unatoč tomu što je digitalni potpis dio računalnog svijeta koji se vrlo brzo mijenja i prihvaća novitete, pri oslanjanju na jedan od algoritama za digitalni potpis važno je razmišljati ne samo o današnjoj računalnoj moći, već i o nadolazećim računalima koja će eventualno biti dovoljno snažna za krivotvorenje potpisa pukom silom (engl. “brute force attack”). Druga, uvijek prisutna neugodna mogućnost je da već danas postoji način “razbijanja” kripto zaštite (isto tako i digitalnih potpisa) pomoću nekih brzih metoda faktoriziranja (velikih) prim brojeva, koje bi tad ugrozile ne samo kripto zaštitu algoritmima poput danas najraširenijeg RSA, već bi vrlo lako osporile i digitalne potpise (načinjene s RSA ili sličnim algoritmom). Ipak, dok se to ne dogodi (ako se ikad dogodi), ostaje nam vjerovati saznanjima današnje matematike koja kaže da je digitalni potpis praktički neprobojan ne samo danas, već i za desetljeća koja dolaze.LITERATURA:
Slika 1. Princip digitalnog potpisa (http://images.google.hr/images?hl=hr&q=digitalni+potpis&um=1&ie=UTF-8&sa=N&tab=wi, 23.03.2008.)
Slika 2. Princip potpisivanja poruke (http://images.google.hr/images?hl=hr&q=digitalni+potpis&um=1&ie=UTF-8&sa=N&tab=wi, 23.03.2008.)
Slika 3. Uspješni završetak dogovora o digitalnom potpisu (http://images.google.hr/images?hl=hr&q=digitalni+potpis&um=1&ie=UTF-8&sa=N&tab=wi, 23.03.2008)
Wikipedija- slobodna enciklopedija (23.03.2008)http://hr.wikipedia.org/wiki/Kriptografija
Besplatni Seminarski Radovi