FIZIKA

Opšte o fizici

Fizika je jedna od fundamentalnih prirodnih nauka koja se bavi proučavanjem građe i opštih svojstava materije. Ona izučava opšte oblike kretanja materije i njihove uzajamne transformacije. U materijalnom svetu nema mirovanja, sve je u stalnom kretanju, a kretanje je način postojanja materije. Apsolutne su samo promene kojima podleže ceo materijalni svet. Otuda su na izgled jednostavni problemi, kojima se fizika bavi, dosta komplikovani. Navedimo samo da svako telo ima mnogo osobina, a svaka osobina je okarakterisana sa više parametara, što ukazuje na veliku složenost najjednostavnijih problema vezanih za proučavanje svojstava materije. Fizičke pojave se opisuju fizičkim zakonima. Neki od ovih zakona su praktično neograničeni, tj. univerzalnog su karaktera. Ovakvi zakoni – principi u fizici se nazivaju osnovnim i oni važe za ceo materijalni svet. Tako se zakonu gravitacije pokoravaju sva zemaljska i vanzemaljska tela, a zakonu održanja energije podčinjavaju se svi do sada poznati procesi.
U svom razvoju, fizika se koristila dostignućima drugih nauka, kao što su njena otkrića koristila drugim naukama i tehnici. Većina tehničkih disciplina razvila se iz odgovarajućih oblasti fizike.
U dvadesetom veku, a naročito posle drugog svetsokg rata, fizika je doživela izuzetno dinamičan razvoj. Pojedine oblasti fizike toliko su se razvile da su postale predmet posebnog izučavanja. Navešćemo samo neke od njih: fizika čvrstog stanja, jonska fizika, atomska fizika, molekularna fizika itd. Svaka od njih je opisana na više hiljada strana, a svake godine iz više raznih instituta sveta, objave se hiljade novih članaka iz svake od ovih oblasti.
Pojavom interneta omogućeno je onima koji se bave naukom da veoma brzo dođu do saznanja o najnovijim otkrićima. Sigurno da ovakav razvoj fizike dovoljno potvrđuje njen značaj.

1. FIZIČKE VELIČINE I JEDINICE. SI SISTEM JEDINICA

1.1 Fizičke veličine

Svaki sistem opisuje se određenim brojem adekvatno odabranih i višestrano precizno definisanih fizičkih veličina. Svakoj veličini pridružuje se određeni simbol i ime. Pod tim simbolom i imenom se tada podrazumeva skup definisanih operacija na sistemu koje konačno dovode do pridruživanja određene brojne vrednosti toj veličini, odnosno simbolu. Ova precedura pridruživanja brojnih vrednosti veličinama naziva se merenjem. Veze među veličinama sada mogu da se izraze matematički, simboli mogu da ulaze u matematičke izraze i dalje da se sa njima postupa po pravilima matematičke logike.
Veličinu možemo definisati kao osobinu pojava (stanja ili procesa), tela ili supstance koje mogu da se razlikuju kvalitativno i da se odrede kvantitativno. Na primer, veličine u opštem smislu su:

• Dužina
• Vreme
• Masa
• Gustina
• Snaga
• Temperatura
• Količina toplote
• Električna otpornost itd.

Veličine u određenom smislu su:

• Dužina letve (traži se dužina određenog predmeta)
• Električna otpornost žice
• Temperatura Sunca itd.

Uticajne veličine su veličine koje nisu predmet merenja ali utiču na vrednost merenja veličina ili na prikazivanje mernog instrumenta.

1.2 Vrednost veličine

Vrednost veličine npr. A određena je prozvodom njene brojne vrednosti {A} i njene merne jedinice [A], tj.
A = {A} · [A]
Na primer: dužina grede je l = 10m, masa tereta iznosi m = 300kg, temperatura vode u bazenu je t = 20ºC itd. pri čemu su: 10, 300 i 20, brojne vrednosti posmatranih veličina, dok su: m, kg i ºC, njihove merne jedinice.
Prava vrednost veličine je veličina koju karakteristiše veličina potpuno definisana u uslovima koji su postojali kada je ova vrednost određena.
Ona se obeležava indeksom t, prema engleskom nazivu (true), npr. Xt, Vt i idealizovana je u pojam.
Može se reći da je prava vrednost Međunarodnog prototipa kilograma, koji je deponovan u Međunarodnom birou za tipove i mere, po definiciji i u određenim uslovima, jednaka tačno 1 kg.

- Trenutna vrednost veličine -

Trenutna vrednost veličine je vrednost neke veličine izmerene u datom trenutku, a lokalna vrednost veličine je vrednost neke veličine vezana za određeni lokalitet. Npr. ubrzanje slobodnog padanja u Beogradu izonsi 9,806 m/s2, a u Zagrebu 9,807 m/s2.
Navedimo još jednu bitnu razliku između rezultata u fizici i matematici, matematičke veličine se mogu izračunavati proizvoljno tačno (princip beskonačno tačno), u fizičkom merenju se može odrediti samo interval u kome se data fizička veličina nalazi. Ilustrujmo to na primer broja π, koji matematičari nazivaju transcadentnim (što znači da se on ne može izraziti ni kao količnik dva prosta broja niti kao koren nekog decimalnog broja). Proveravanjem u tablici zaključujemo da se vrednost broja π nalazi u intervalu 3,141 < π < 3,142. Dužina ovog intervala je 0,001. Uzimajući u obzir sledeće brojke, možemo napisati:
3,1415 < π < 3,1416
čime smo dužinu intervala smanjili deset puta. Postupak sužavanja intervala možemo produžiti po želji, zato i kažemo da se broj π može bar u principu tačno odrediti. Posle beskonačno mnogo koraka dužina intervala će biti nula, što znači da je vrednost broja π tačno određena.

1.3 Sisitem veličina

Sistem veličina je skup koji čini data grupa osnovnih veličina i odgovarajućih izvedenih veličina i koji obuhvata sve oblasti nauke.
Osnovne veličine su veličine koje su, u datom sistemu veličina prihvaćene kao međusobno nezavisne i pomoću kojih se ostale mogu izraziti jednačinama koje ih povezuju. Na primer u SI sistemu su osnovne veličine: dužina, masa vreme itd.
Izvedene veličine su veličine koje su definisane kao funkcija osnovnih veličina tog sistema, na primer: brzina, ubrzanje, sila itd.

1.4 Dimenziona analiza

Dimenzija veličine je izraz koji definiše određenu veličinu nekog sistema kao proizvod osnovnih veličina tog sistema, uz naznaku odgovarajućih izložitelja.

1.5 SI sistem jedinica

Merna jedinica (jedinica mere) je vrednost neke veličine za koju je dogovorom usvojeno da ima brojnu vrednost 1. Oznaka merne jedinice je dogovorena oznaka koja označava mernu jedinicu posmatrane veličine. Osnovna merna jedinica je merna jedinica jedne od osnovnih fizičkih veličina. Izvedena merna jedinica je merna jedinica izvedene veličine.

- Međunarodni sistem jedinica (SI) -

Sada je u upotrebi mahom Međunarodni sistem jedinica (SI), zasnovan na sledećih sedam osnovnih jedinica.

Metar               (m)         jedinica za dužinu
Kilogram         (kg)        jedinica za masu
Sekunda           (s)          jedinica za vreme
Amper             (A)         jedinica za jačina elek. struje
Kelvin             (K)         jedinica za termodinamičku temaparaturu
Kandela           (cd)        jedinica za jačinu svetlosti
Mol                 (mol)      jedinica za količinu supstance

- Dopunske jedinice -

Radijan                            jedinica za ugao u ravni
Steradijan                        jedinica za prostorni ugao

2. MERENJE I REZULTATI MERENJA

2.1 Pojam merenja

Merenje je skup eksperimentalnih operacija čije je cilj određivanje vrednosti neke veličine. Da bi se merenje izvelo mora postojati jedinica mere za svaku fizičku veličinu + proceduru za upoređivanje vrednosti fizičke veličine sa tom jedinicom mere. Zbog prvog zahteva postoji čitav niz sistema jedinica, a zbog drugog veliki broj instrumenata i metoda za merenje svake veličine, kao i način za realizaciju samih jedinica mere.
Merenje možemo definisati i kao operaciju (postupak ili niz postupaka) kojom se neka veličina neposredno ili posredno upoređuje sa veličinom iste vrste koja je izabrana za jedinicu.
Rezultat merenja je broj koji pokazuje koliko odgovarajućih jedinica ima merna veličina iste vrste. Taj broj se naziva brojna vrednost ili merni broj date fizičke veličine.

2.2 Vrste grešaka prema njihovim izvorima

Prema svome izvoru greške se mogu podeliti na:

• Grube greške ili omaške
• Sistematske greške
• Slučajne greške

Omaške su zaista greške u negativnom smislu te reči. Nastaju usled nepažnje eksperimentatora. Kod početnika su veoma česte. Najprostiji primer omaške je kada se zapiše vrednost različit od pročitanog, na primer, umesto izmerene dužine 13,7cm zapiše se 15,7cm. Omaške mogu nastati i kada se matimatičke operacije izvrše pogrešno, tj. pogrešno se pomnože, saberu ili dr.
Gruba greška se može učiniti kada se meri temperatura tečnosti. Ako smo tečnost zagrevali na rešou i nedavno skinuli sa njega, zidovi suda mogu da budu topliji od tečnosti. Ako termometar slučajno dodirne zidove suda pokazaće veću temperaturu od temperature tečnosti.
Paralaksa je tipičan primer omaške. Ona se sastoji u tome da pokazivanje kazaljke instrumenata zavisi od položaja oka.

Sistematske greške predstavljaju odstupanje uvek u istom smislu. Veličina i znak sistematske greške su iste kod svakog merenja istim priborom. Ako se meri pomoću instrumenta čija je skala pomerena, pročitana vrednost će se uvek razlikovati od „stvarne“ za istu vrednost. Na primer, ako dužinu merimo lenjirom čiji je početak odsečen, pa skala umesto „0“ počinje sa 2cm, pri merenju ćemu uvek dobiti za 2cm dužinu veću od stvarne.
Ovaj primer greške koji je nastao usled osobine instrumenta može se nazvati greškom instrumenta.

Slučajne greške (statističke, neizbežne greške), iz naziva bi se moglo zaključiti da su to greške bez uzroka. One imaju svoje uzroke ali su oni često nepoznati, a što je važnije ove greške se mogu tretirati statističnim metodama (ponekad se nazivaju metodama slučajnih događaja).
Faktički to su greške koje nastaju zbog mnoštva malih efekata koje se ne mogu kontrolisati. Kao na primer, uticaj temperature na merni instrument, vlažnost vazduha, nestabilnost napona mreže, mehaničke oscilacije aparata itd.

Apsolutna greška je odstupanje merne od stvarne vrednosti.

Δx = | x – χ |

Δ – apsolutna greška
x – stvarna veličina
χ – merna veličina

pa rešavanjem dobijamo da je x = χ ± Δx

Za karakteristiku tačnosti izmerenih veličina uvodi se nova veličina, tj. relativna greška, jednačinom:

Tj. relativna greška je odnos apsolutne greške prema izmerenoj veličini.

3. OBRADA REZULTATA MERENJA

3.1 Rezultati merenja i zaokruživanje

Formalno gledano, svaki rezultat merenja se predstavlja u obliku zagrade u kome piše rezultat merenja ± gornja granica apsolutnog odstupanja, a izvan zagrade se pišu i njegove jedinice.
Konačni rezultat indirektnog merenja ne može da bude tačniji od najtačnije (direktnim putem) izmerene veličine. Na primer, gustinu nekog predmeta, zapreminu izmerimo pomoću menzure i ona je V = (5 ± 1)m3, a masu vagom i neka je m = (30,22 ± 0,01)g. Prostim rečima se dobija da smo zapreminu odredili sa tačnošću od 20%, a masu 0,03%.

Tj. gustina

Niz merenja iste veličine, ne mora dati uvek isti rezultat, što je posledica postojanja slučajnih grešaka. Neka su merenjem mase izvesnog tela dobijeni sledeći rezultati:

m1 = 5,24g
m2 = 5,27g
m3 = 5,23g
m4 = 5,25g

U svim ovim rezultatima prve dve cifre se stalno ponavljaju, dok se treća cifra menja od merenja do merenja. One cifre koje se u rezultatima ne menjaju, nazivaju se sigurne (tačne) cifre, a one promenjljive zovu se nesigurne (sumnjive) cifre. Rezultat merenja izražava se pomoću svih sigurnih cifara i najviše jedne (naravno prve) nesigurne cifre.

Pri obradi rezultata merenja često treba zaokružiti brojeve, pa ćemo zbog toga navesti poznata pravila zaokruživanja:

• Ako je na prvom zanemarenom decimalnom mestu cifra veća ili jednaka 5, a iza njega ima značajnih cifara različitih od 0, poslednja cifra se povećava za 1;

12,156 ≈ 12,2

• Ako je cifra na prvom zanemarenom decimalnom mestu manja od 5, predhodna cifra se ne menja;

1,346 ≈ 1,3

• Ako je prva cifra koja se zanemaruje 5, a iza nje nema značajnih cifara različitih od 0, onda se poslednja zadržana cifra povećava za 1, ako je ona neparna, a ostavlja se nepromenjena ako je parna;

1,350 ≈ 1,4
1,450 ≈ 1,4

Iz svega iznesenog znači da, tačnost rezultata ne zavisi od broja značajnih nego od broja sigurnih cifara.

3.2 Direktno merenje koje se ne ponavlja

Ako je tačnost instrumenta manja od statističkih grešaka, onda nema smisla ponavljati merenje. Tj. ako vidimo da se uzastopnim merenjem ne menja rezultat, treba prekinuti sa daljim merenjima.

Nominalne tačnosti nekih instrumenata

3.3 Indirektno merenje

Je gornja granica apsolutnog odstupanja veličine koja se dobije sabiranjem direktno mernih veličina. Na primer kada se meri dužina predmeta lenjirom kraćim od samog predmeta.
Procena tačnosti rezultata merenja koji se dobije kao količnik složenijeg izraza:

r =             (a i b merne veličine)

4. PRIKAZIVANJE REZULTATA MERENJA

Merenje se sastoji iz niza direktnih merenja, a ovaj niz možemo prikazati:

• tabelarno
• grafički

4.1 Tabelarno prikazivanje rezultata

Tabela je šema koja služi za pregledno i sistemsko upisivanje većeg broja podataka. Rubrike u tabeli se popunjavaju brojnim vrednostima izmerenih podataka i tekstom.
Tabele treba pripremiti pre merenja tako da se tokom merenja popunjavaju samo rubrike.
Primer instrumenta za merenje odnosa mase i istezanja opruge.

4.2. Grafičko prikazivanje rezultata

Grafičko prikazivanje rezultata ima tu prednost da se priroda zavisnosti može direktno vizuelno uočiti. Osim toga na grafiku se mogu uporediti i više krivih.

4.3. Linearizacija grafika

Linearizaciju grafika je moguće izvršiti u slučajevima kada je poznat oblik fizičkog zakona koji povezuje dve veličine (na primer iz teorije) ,bez čega je problem linearizacije često nerešiv.
Oblik onih zavisnosti F(x,y) koji se često sreću u fizici kao njihovu linearizaciju dato je u tabeli 4.3.1.

5. ODREĐIVANJE UBRZANJA SLOBODNOG PADANJA

Na osnovu zakona gravitacije, Zemlja privlači sva tela u njenoj blizini konstantnom silom usmerenom ka njenom centru. Kada je sila konstantna, konstantno je i ubrzanje, pa odavde proizilazi da sva tela padaju na zemlju sa istim ubrzanjem. Ustvari, ubrzanje koje telo mase (m) dobija se:

a =  gde je F sila kojom Zemlja privlači.

Imajući u vidu Njutnov zakon gravitacije dobijamo:

a =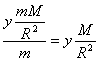

M – masa Zemlje
R – poluprečnik Zemlje

Pošto su masa Zemlje i poluprečnik Zemlje konstantne, konstantno je i ubrzanje kojim telo pada na zemlju. Obeležava se sa q i naziva se ubrzanje Zemljine teže ili gravitaciono ubrzanje.

g =

Ako se telo nalazi na polu Zemlje nema utecaja zemljine rotacije oko sopstvene ose. Znači, sila kojom Zemlja privlači tela naziva se sila zemljine teže i označava se sa:

= m ·g

1.1 Gravitacino polje

Prostor u kome se osjeća dejstvo gravitacione sile predstavlja gravitaciono polje. Gravitaciono polje se može prikazati pomoću gravitacionih linija sila i može se okarekterisati jačinom gravitacionog polja i potencijala.
Gravitaciono polje postoji i u telu.
Jačina gravitacionog polja u nekoj tački je brojno jednaka sili po jediničnoj masi.

1.2 Gravitaciono ubrzanje

Gravitaciono ubrzanje nema istu vrednost na različitim mjestima u Zemlji, na i iznad Zemlje. Ova razlika dolazi usled nejednakosti zemljinih poluprečnika (na polu i Ekvatoru razlika u poluprečniku je oko 40km).
Gravitaciono ubrzanje na polu iznosi:

Na ekvatoru (E) usled rotacije Zemlje gravitaciono ubrzanje se smanjuje za veličinu koja potiče usled rotacije Zemlje oko svoje ose odnosno usled centrifugalne sile:

sa slike φ

Imajući u vidu, za izraz gravitacionog ubrzanja na površini Zemlje na bilo kojoj geografskoj širini dobijemo:
φ

LITERATURA

• Dr. V. Sajfert: Praktikum iz fizike, TF „M. Pupin“, Zrenjanin, 2002
• Dr. V. Sajfert: Zbirka zadataka iz fizike, TF „M. Pupin“,  Zrenjanin, 2002
• Dr. V. Sajfert: Fizika, TF „Mihajlo Pupin“, Zrenjanin, 2003
• V. Bego: Mjerenja u elektrotehnici, Tehnička knjiga, Zagreb, 1981
• V. Hajro: Zbirka vežbi iz električnih merenja, Tehnička knjiga, Beograd, 1973
• V. Jovanović: Električna merenja, Naučna knjiga, Beograd, 1967
• D. Pertović: Električni merni instrumenti i njihova primena, Tehnička knjiga, Beograd, 1981
• D. Martinović: Električna merenja, Zavod za udžbenike i nastavna sredstva, Beograd, 2000

  preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi