BLAISE PASCAL

3. Pascalova biografija

 Kudikamo je bolje znati o svakoj stvari ponešto nego o jednoj sve. (Blaise Pascal)

Slika 1. Blaise Pascal

Francuski filozof, matematičar i fizičar Blaise Pascal rođen je 19. juna 1623. u mjestu Clermont-Ferrand (Klermont-Feran) u braku Antoinette (rođ. Begon) i Étiennea Pascala. U razmaku od šest godina dobili su četvero djece od kojih je prvo (djevojčica) umrla veoma rano. U životu su ostali Gilberta, Blaise i Jaqueline zvana Jaquete (Žaket). Jacquete će kasnije postati samostanska redovnica Eufemia. Kada je Blaiseu bilo tri godine (1626.) umire njegova majka, a njegov otac (lokalni sudac i ugledan čovjek) unajmljuje guvernantu Louis Belfaux (Lujza Belfo). Ona je skrbila o djeci dok se Étienne brinuo za odgoj, a kasnije i obrazovanje. Još u dječačkoj dobi Blaise će iskazati veliku volju za učenjem što će njegov otac rado podržati.Ipak privilegirani položaj kod otac tada još imala Jacquelina koje je s osam godina slovila kao pjesnikinja, a s 13 godina napisala je sonet posvećene kraljici. Kasnije će u Rouenu (Ruan) dobiti čak i nagradu na jednom poetskom turniru. Nešto kasnije njezina darovitost odigrati će značajnu ulogu u tome da njezin otac ponovno dobije naklonost kardinala Richelieua (Rišilje). Skrbeći o kćerkinu pjesničkom daru Étienne je nastojao da Blaise najprije dobro načui latinsk i grčki jezik. Matematičke udžbenike je sklonio smatrajući kako će matematika njegova sina zavesti na pogrešan put i spriječiti u humanističkoj naobrazbi. Blaise se ipak sam približio geometriji stvorivši, prema svjedočenju sestre Gilberte, neke aksiome Euklidove geometrije uopće je ne poznavajući. Otac je bio istovremeno zapanjen i oduševljen te je odlučio sinu nabaviti knjige iz geometrije kako bi se njegov genij mogao dalje razvijati. S 11 godina Blaise je otkrio neke osobine zvuka kada je slučajno ispustio nož na tanjur, a odmah potom uhvatio porculan kako bi prigušio zvuk rukom.
No, otac nije promijenio svoju odluku da sina ne šalje u školu već ga je i dalje nastavio sam podučavati. U njegovom konceptu obrazovanja značajni su bili susreti sa znanstvenicima onog vremena koji su se kretali u krugu umnog opata Mersena, a on se dopisivao s Galilejem i Descartesom. Tu će Pascal uskoro zadobiti simpatije gostiju i sklopiti poznanstvo s matematičarem Pierre de Fermatom, s kojim će stvoriti temelje računa vjerovatnoće i s fizičarem Robervalom koji će utjecati na njegovo kasnije bavljenje problemima težine. Ali sigurno je da je očev utjecaj na Blaisea bio najveći. On ga je i poštivao i volio. Prihvatio je njegove poglede na život i znanost, pokušavao ga je slijediti sve dok nije pronašao sebe i nastavio napredovati u smjeru gdje ga otac više nije mogao voditi. Prvi značajan rad Pascal je napisao sa 16 godina. Bio je to osnovni nacrt njegove rasprave o konusnim presjecima, koja će se kasnije izgubiti, ali koju će vidjeti Leibniz kad je Pascalu bio 19 godina. Leibniz je u početku sumnjao da je takvo djelo mogao napisati šesnaestogodišnjak. Ipak sa šesnaest godina Blaise je stvorio i svoj mistični heksagram koji nije sačuvan. Tim svojim mladalačkim radovima Blaise je već stekao glas ozbiljnog znanstvenika u kog su polagane velike nade. Svoje prvo djelo, Esej o konikama, Blaise Pascal je objavio godinu dana kasnije 1640, a s konikama i projektivnom geometrijom bavio se i u kasnijim razdobljima svog života te se uz Desarguesa smatra utemeljiteljem projektivne geometrije .U isto doba Pascal se počinje baviti i fizikom. Tako je 1647. dokazao postojanje vakuuma. Nakon toga se susreo s Descartesom, koji nije vjerovao u postojanje vakuuma, te je poslije susreta u pismu Huygensu napisao da Blaise Pascal ”. . . ima previše vakuuma u glavi”.Pascal se tokom ljeta 1654. dopisivao s de Fermatom, a iz te korespondencije nastala je savremena teorija vjerojatnosti.Pascal je za dobivanje rješenja iskoristio aritmetički trokut poznat kao Pascalov trokut. U oktobru iste godine zamalo je izgubio život u nezgodi, kad su se konji koji su vukli njegovu kočiju uplašili te je kočija ostala visjeti na mostu nad Seinom. U ovom razdoblju pisao je filozofska djela, od kojihje najznamenitije  ''Misli'' ,skup osobnih razmišljanja o ljudskoj patnji.
Etienne Pascal je prolazio kroz iskušenja svog vremena, u kome se bilo veoma teško snaći, pravilno odrediti i tako izbjeći srdžbu kancelara ili kralja. Kako bi izbjegao tamnicu morao je 1638. napustiti Pariz i povući se na svoje imanje u Clermont-Ferrandu i to stoga što se pridružio prosvjedu pravnika protiv Richelieuove odluke o povećanju poreza. Da bi oca vratila u državnu službu Jaqueline je prihvatila ponuđenu ulogu u kazališnom komadu ''Tiranska ljubav''. Poslije predstave je izrecitirala svoj sonet u pohvalu kardinalu,a on je zauzvrat dopustio da nešto poželi. Ona je zatražila milost za oca, što je kardinal odmah prihvatio. Tako se Étienne Pascal vratio u državnu službu dobivši mjesto poreznika u Normandiji. Ali nije bilo sve tako lako jer trebalo je doći u normandijsku prijestolnicu Rouen koji je zauzela vojska tzv. bosonogih (preglednjelih, bijednih, skitnica, prosjaka i ubožnika). Nakon više od godinu dana slamanja otpora francuska je vojska, a zajedno s njom i Étienne s obitelji (koju je uvijek vodio sa sobom) 1640. ući u grad.
S ovim problemom na planu praktične primjene matematičko-fizičkih znanja dolazi i Blaiseova bolest. Glavobolje postaju stalne, a njima se pridružuje bolest želuca praćena kratkotrajnom paralizom udova. Od svoje 19 godine Blaise živi s glavoboljom i nesanicom, a s vremenom postaje još gore. Od 24 godine nije mogao piti hladnu tečnost, a i mlako je mogao uzimati samo kap po kap. Za promatrača to je bio veoma mučan prizor, dok se on stoički odnosio prema svojoj bolesti. Nikada se nije žalio. Ma o čemu bila riječ Blaise je veoma brzo uspijevao na blag i jednostavan način sve prisutne privoljeti da ga slijede i slušaju bez komentara i prigovora. Njegov duh je posjedovao nešto što nije moglo imati protivnika. Moglo se ili primiti ili potpuno odbaciti, ali se s njegovim argumentima nije se moglo sporiti. Nastojeći popraviti njegovo zdravlje, liječnici su mu savjetovali da manje izlaže svoj um prevelikim naporima vezanim za matematiku ili neku drugo područje, što je bio uzaludan zahtjev. Radoznao i živ duh u vrijeme očevog službovanja u Rouenu trošio je dane i na besposlicu. Često se družio sa svojim prijateljima koji će ga jednog dana odvesti i do čudnog kapucina Jacques Fortona. Mistično učenje ovog kapucina dovesti će do toga da ga Blaise prijavi vrhovnim crkvenim vlastima. Boreći se protiv Fortona Blaise će pod utjecajem Descartesa stvoriti kasnije nacrt svoje Apologije kršćanstva. Godine 1646. prekretnica je u Pascalovom životu, od te godine intenzivno se
posvećuje vjeri i filozofiji. Povod prekretnici je bila očeva ozljeda nakon koje su
ga njegovala dva brata iz jednog vjerskog pokreta koji su ostavili dubok dojam na PascalaOni sa sobom donose neobično učenje Saint-Cyrana (Sen Sirana) i Jansenovu doktrinu, poznatu kao jansenizam . Bilo je to preobraćenje cijele obitelji. Naročito je novo učenje prihvatila Jaqueline te će ona uskoro pristupiti časnim sestrama u Por-Roayalu. Jansenističko učenje baziralo se na milosti koju treba očekivati od Boga te je zato potrebno živjeti skromno i skrušeno, daleko od ljudske gomile, lišiti se komfora, prezreti jezuite i njihove opačine. Takvi su pogledi brzo došli pod udar zvanične Crkve, a izopćenje Janseinusa i stavljanje njegovog djela na indeks zabranjenih knjiga bio je početak njihova kraja.

Sve to utječe na dalje približavanje Blaisea jansenizmu. Jaqueline traži od oca dopuštenje da se potpuno povuče u samostan, ali on ne pristaje. Na brata vrši pritisak da se ostavi nauke i dosadašnjeg načina živote te se u potpunosti posveti vjeri. Blaise ipak ne popušta već nastavlja živjeti kako je volio u društvu lijepih žena i vina pokušavajući tako zaboraviti na svoje tjelesne patnje. Kada umire otac (1651.) Blaise postaje glava kuće, a Jaquelina pokušava nagovoriti brata da joj dopusti zaređenje. Slijedeći misao oca i on odbija sestri dopustiti zaređenje te se prepušta vedrom pariškom društvu zajedno s pravnikom Domaom. Njih dvojica posjećuju salone gospođa Dagijon, Longeville i de Sable. U tim druženjima postaje intiman prijatelj s vojvodom od Roanneza, zaljubljenikom u matematiku te s kockarom i vitezom Chevalier de Mereom koji će navesti, tražeći da se on pozabavi mogućnošću dobitka na kartama, da stvori svoju matematičku teoriju vjerovatnoće. Na koncu sestri konačno dopušta da se zaredi. Ujedno, kako način života koji je živio, nije jeftin sve više razmišlja o povlačenju na svoje imanje ili neko drugo mjesto.Tih je godina u punom matematičkom zanosu. Dopisuje se s de Fermatom, obajvljuje radove o tečnosti i prenošenju tlaka kroz tečnost te upućuje pregled svog znanstvenog rada Pariškoj akademiji. Potom se odlučuje povući u samostan Por-Roayal gdje boravi u društvu tzv. usamljenika. Tu razmišlja o jansenizmu i problemima vjere, nastojeći na neki način obraniti jansenizam od napada sa Sorbone . Ne upušta se u teološke rasprave nego pokreće pitanja morala i istine. Tako nastaju njegova čuvena pisma upućena jednom provincijalu, koja su dočekana s velikim iznenađenjem, ali i s osudom crkvenih dostojanstvenika. Ne prekidajući potpuno naučni rad obajvljuje svoj rad o cikloidi , koji je navodno nastao jedne noći kada ga mučila žestoka zubobolja. Pronašao je rješenje dotad nerješenog problema, a zubobolja je bila kao rukom odnešena. Do kraja života ostale su mu samo četiri godine u kojima je bolove trpio bez jauka zahvaljujući samo svome neshvatljivom asketizmu. Na papirićima zapisuje svoje misli i stavlja ih u jednu jastučnicu. Posljednje godine života umire njegova voljena sestra Jaqueline i uporedo s tim dolazi i do konačne osude jansenizma. Raseljen je Por-Royal, a Blaise potom živi kod druge sestre u Parizu. Nakon dva dana agonije umire u velikim mukama u jedan sat poslije ponoći 19. kolvoza 1662. Iduće godine objavljeni su njegovi matematički radovi o kojima se brinuo njegov prijatelj Jean Doma. Njegov karakter je opisan kao ...

... prerano sazreo i razvijen, tvrdoglav i istrajan, perfekcionista,
borben do granica nemilosrdnosti, krijuci da moze da bude blag i pokoran...

4. Pascalov zakon

Atmosferski pritisak je sila koja deluje okomito na jedinicu  površine, a jednaka je težini stuba vazduha koji se rasprostire od tla do gornje granice atmosfere. On se najčešće mjeri živinim barometrom, u kome se visina živinog stuba uravnotežuje sa težinom vazdušnog stuba, i izražava se u milimetrima (mm) ili milibarima (mb).
Paskal (znak: Pa) je mjerna jedinica za pritisak u Međunarodnom sistemu jedinica (SI) Iznosi 1 njutn po kvadratnom metru (1N/m2). Jedinica je nazvana u čast Blaisea Pascala.U svom tekstu Treatise on the Equilibrium of Liquids (1653) objavljuje svoju teoriju o pritisku tj.formuliše osnovni zakon hidrostatike:
Djelujemo li na tekućinu u ravnoteži izvana nekom silom F, tada se taj vanjski pritisak širi u tekućini jednako na sve strane. Npr. ako na posudu napunjenu vodom preko klipa površine S djelujemo vanjskom silom F, sila se fluidom prenosi u svim smjerovima tako da se pritisak p, koji stvara vanjska sila, pojavljuje u svim tačkama fluida pa vrijedi:

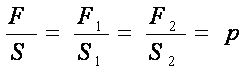
To je Pascalov zakon za vanjski (ili hidraulički) pritisak: U svakoj tački mirnog fluida pritisak je jednak.

Slika 2. Pascalov zakon

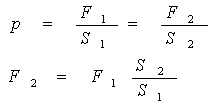
 Na ovom principu se temelje hidraulički uređaji: preša, kočnice, dizalice...

5. Pascalov teorem o mističnom heksogramu

Kad je Blaise imao šesnaest godina na jednom je sastanku Mersenneove grupe prezentirao komad papira na kojem je naveo nekoliko teorema
projektivne geometrije koje je sam dokazao, a od kojih je najpoznatiji Pascalov teorem o mističnom heksagonu. Taj teorem kaže: ako na krivulji drugog reda, recimo na elipsi, označimo šest tačaka u redoslijedu 1,2,3,4,5,6 (bitan je redoslijed označivanja, nije nužno da spajanje točaka u tom redoslijedu daje šesterokut), onda su sjecišta A, B, C parova pravaca 12 i 45, 23 i 56, 34 i 61 su medusobno kolinearna:

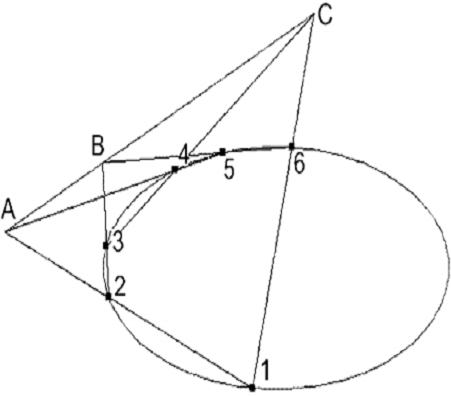
Slika 3. Heksogram

6. Pascaline

Pascalina mehanički stroj s mnoštvo zupčanika koji je mogao zbrajati i oduzimati velike brojeve.Konstruirao ga je Blasie Pascal 1645. kako bi olakšao posao svom ocu porezniku. Pascalina je mogla raditi s brojevima do 9 999 999.Radove na stroju je započeo Pascal 1642. koji tada nije imao ni devetnaest godina.Bio je to prvi takav stroj nakon stroja za računanje kojeg je izradio Wiliam Schickard. Godine 1649. dobio je kraljevsku povlasticu koja mu je jamčila ekskluzivno pravo prodaje stroja u Francuskoj.

Slika 4. Pascaline

Pascal je proizveo pedesetak protutipova stroja,ali je proizvodnju prekinuo zbog slabe prodaje.Prodao ih je petnaestak. Taj će stroj kasnije, potpuno usavršen, i poklonjen Chiristini švedskoj, koja sa nije udostojila ni odgovora.
 

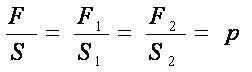
7. Teorija vjerovatnoce

Pascal se tokom ljeta 1654. dopisivao s de Fermatom, a iz te korespondencije nastala je savremena teorija vjerojatnosti. U pet pisama Pascal i de Fermat su proučili već prije poznate kockarske probleme: problem dvije kocke i problem podjele uloga. Te je probleme Pascalu postavio prijatelj, kockar Chevalier de Mere, a Pascal i de Fermat su riješili oba problema.U pet pisama Pascal i de Fermat su proučili već prije poznat kockarske probleme: problem dvije kocke i problem podjele uloga.Problem dvije kocke sastoji se u pitanju koliko puta treba baciti par kocaka da bise isplatilo kladiti da će bar jednom pasti par šestica. Konkretno, isplati li se kladiti da će u 24 bacanja para kocaka bar jednom pasti par šestica? Taj je problem lako rješiv, kako je pokazao Pascal: vjerojatnost da će u jednom bacanju pasti par šestica je 1/36 ≈ 2, 78% jer je samo jedna od 36 mogućh kombinacija ”broj na prvoj kocki - broj na drugog kocki” odgovarajuća. Stoga je vjerojatnost da u jednom bacanju neće pasti par šestica jednaka p = 35/36 ≈ 97, 22%. Svako bacanje je nezavisno od prethodnog, pa se za dobivanje vjerojatnosti da u n bacanja nijednom ne padne par šestica p treba n puta množiti sam sa sobom: P = p24 ≈ 50, 86% je vjerojatnost da u 24 bacanja nijednom ne padne par šestica. Kako će u 24 bacanja ili bar jednom pasti ili nijednom ne pasti par šestica, znači da je vjerojatnost da par šestica bar jednom padne 1 − P ≈ 49, 14% tj. ne isplati se kladiti da će u 24 bacanja para
kocaka bar jednom pasti par šestica.
Zanimljiviji je problem podjele uloga: dva igrača igraju neku igru koja se igra po krugovima sve dok jedan ne ostvari zadani broj pobjeda, recimo 3. U nekom trenutku prije kraja, recimo pri stanju bodova 2 : 1, igrači žele prekinuti igru. Pitanje je u kojem omjeru trebaju podijeliti ulog (recimo da su oba uložila po 32 kn). U pismima su se Pascal i de Fermat suglasili oko odgovora, no dali su različite dokaze. Pascalov pristup je idući: da su igrali još jedan krug, rezultat bi bio ili 3 : 1 (u kojem slučaju prvi dobiva 64 kn) ili 2 : 2 (u kojem slučaju treba igrati još jedan krug ili se mogu suglasiti da svaki uzme po 32 kn). Stoga prvi igrač može reći da je siguran u dobitak 32 kn, a što se druge 32 kn tiče, šansa je pola-pola da će ih dobiti tj. od njih bi trebao dobiti pola. Stoga Pascal zaključuje da je pravedna podjela uloga 48 kn prvom i 16 kn drugom igraču. Pascal je analizirao i slučaj da je stanje pri prekidu bilo 2 : 0 (dobiva se omjer 56 kn : 8 kn) ili 1 : 0 (dobiva se omjer 44 kn : 20 kn).
Pascal i de Fermat su problem razmotrili i u općenitijem slučaju. Recimo da je za pobjedu potrebno m + n bodova ukupno, a igra je prekinuta pri stanju m : n. U pismu Pascalu iz kolovoza 1654. de Fermat kaže da ako prvom igraču do pobjede manjkaju 2 boda, a drugom 3, igra bi u najduljoj varijanti trajala još 4 kruga (uvjerite se u to!). Uzmimo dva slova, recimo a i b, kao oznake pobjede prvog odnosno drugog u pojedinom krugu. Svi nizovi duljine 4 koje možemo složiti od ta dva slova predstavljaju sve moguće redosljede pobjeda u ta 4 dodatna kruga.
To su aaaa, aaab, aaba, aabb, abaa, abab, abba, abbb, baaa, baab, baba, babb, bbaa, bbab, bbba, bbbb, ukupno njih 16. Svaki niz s bar dva a predstavlja situaciju u kojoj pobjeduje prvi igrač, a oni s bar tri b su u korist b. Prebrajanjem vidimo da prvi pobjeduje u 11, a drugi u 5 od tih 16 slučajeva. Pascal je za dobivanje rješenja iskoristio aritmetički trokut poznat kao Pascalov trokut.

Pascalov trokut bio je nekoliko stotina godina ranije poznat Kinezima i Arapima, no Pascalovo djelo Rasprava o aritmetičku
(1665)je prvo detaljnije proučavanje tog trokuta. Pascalov trokut je trokutasta tablica binomnih koeficijenata. Pascal ju je zapisivao kao pravokutnu:

1 1 1 1 1 . . .
1 2 3 4 5 . . .
1 3 6 10 15 . . .
1 4 10 20 35 . . .
1 5 15 35 70 . . .
...
...
...
...
...

U prvom retku i stupcu su samo jedinice, a ostali brojevi nastaju tako da zbrojimo brojeve lijevo od i iznad pozicije na koju unosimo novi broj. Danas je uobičajno tu tablicu pisati u trokutastom obliku

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
...
...

U ovakvom zapisu, rubovi su jedinice, a element na nekoj poziciji je zbroj dva elementa iznad njega. Ako za Pascalovu (pravokutnu) tablicu indeks retka promatranog broja označimo sa i, a indeks njegova stupca sa j, te ako je broj u i-tom retku, j-tom stupcu jednak pi+1,j+1 pravilo kojim se zbrajanjem dobivaju brojevi glasi

pi+1,j+1 = pi+1,j + pi,j+1.

 Iz ovog slijedi: svaki broj (npr. broj 20 na poziciji 4. redak, 4. stupac) je jednak zbroju brojeva u stupcu lijevo od njega od prvog
do njegovog retka u našem slučaju 20 = (1 + 3 + 6 + 10). Pascal je otkrio i niz drugih svojstava ovog trokuta. Danas kažemo: broj pi+1,j+1 je binomni koeficijent vidimo dakle da je Pascalov trokut tablica binomnih koeficijenata. Nalaženje binomnih koeficijenata lakše je u suvremenom trokutastom zapisu
Pascalova trokuta: binomni koeficijent _??????? vom redu. Kako je poznato, binomni koeficijenti su koeficijenti koji se pojavljuju u binomnoj formuli

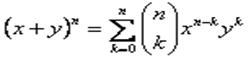
i lako i brzo ih se računa koristeći Pascalov trokut. Tako su koeficijenti za (x +y)3 redom elementi četvrtog retka Pascalova trokuta (zapisanog na suvremeni način): to su 1, 3, 3,1 pa je (x + y)3 = x3 + 3x2y + 3xy2 + y3.
Kako Pascalov trokut iskoristiti u rješavanju problema uloga?
Upotrebom Pascalova trokuta može se izbjeći ispisivanje svih nizova. Tako u opisanom slučaju kojeg je razmatrao de Fermat trebamo pogledati peti redak Pascalova trokuta (zapisanog na suvremeni način) 1, 4, 6, 4, 1. Ti brojevi redom kažu u koliko nizova (duljine 4 sastavljenih od slova a i b) imamo a tačno 4, 3, 2, 1, 0 puta (prvi pobijedi u sva 4 kruga samo u 1 slučaju, prvi pobijedi ukupno 3 kruga u 4 slučaja, prvi pobijedi ukupno 2 kruga u 6 slučajeva, prvi pobijedi u tačno 1 krugu u 4 slučaja, prvi ne pobijedi nijednom u 1 slučaju). Kako za konačnu pobjedu prvog on treba pobijediti
u bar 2 kruga, povoljni za prvog su slučajevi s ukupno 4, 3 ili 2 slova a, a njih ima ukupno 1+4+6 = 11; za drugog su povoljna preostala dva slučaja (slovo a jednom ili nijednom u nizu), a njih ima 4 + 1 = 5. Stoga je omjer u kojem treba podijeliti uloge 11 : 5.

Citati

• Čovjek je samo trska, najslabija u prirodi, ali to je trska koja misli.
• Kad bi svi ljudi znali što jedni o drugima govore, na svijetu ne bi bilo ni četvorice prijatelja.
• Kudikamo je bolje znati o svakoj stvari ponešto nego o jednoj sve.
• Ljubav nema godina, ona se uvijek rađa.
• Onaj tko govori samo lijepe riječi ima loš karakter.
• Pametan čovjek nikad neće reći da sve zna.
• Pravda bez moći je bezmoćna; moć bez pravde je tiranska.
• Znati ne znači biti. Naučeno morate pokušati prenijeti u svakodnevni život.

  preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi