OSTALI SEMINARSKI RADOVI
IZ FIZIKE:
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
OPTIKA
OPTIKA je grana fizike koja proučava svjetlost i osobine svjetlosti, optičke instrumente,sredstva za poboljšanje vida (optička sočiva), ogledala kao i talasnu prirodu svjetlosti.Dijeli se na fizikalnu i opštu geometrijsku.Fizikalna optika se primarno bavi prirodom i osobinama same svjetlosti.
Geometrijska optika se bavi principima koji omogućavaju stvaranje likova i slike preko sočiva, ogledala, prizmi i drugih instrumenata koji koriste svjetlost.
Geometrijska optika zasniva se prvenstveno na zakonima i teorijama geometrije posle usvojenih apstrakcija i aproksimacija, ali osim toga i na fizičkim zakonima od kojih su najvažnija sledeća četiri:
1. Zakon pravolinijskog prostiranja svjetlosti
2. Zakon međusobne nezavisnosti prostiranja svjetlosnih zraka
3. Zakon odbijanja svjetlosti
4. Zakon prelamanja svjetlosti.
U ovom radu će biti obrađena pojava odbijanja svjetlosti od sfernih površina, tj. sfernih ogledala.
INTERFERENCIJA SVJETLOSTI
Sve što je rečeno o interferenciji kod talasnog gibanja važi i za svjetlosne talase. Na osnovi tih razmatranja trebalo bi očekivati da se pri osvjetljivanju neke površine, istovremeno s nekoliko svjetlosnih izvora, kao rezultat interferencije na njoj pojavi interferencija slika s karakterističnim svijetlim i tamnim poljima. Međutim, eksperimenti i svakidašnje iskustvo ukazuju na to da do te pojave ne dolazi. To se objašnjava činjenicom da se interferencija kod svjetlosti može ostvariti samo pod posebnim uslovima i s koherentnim svjetlosnim izvorima.
Dva ili više različitih prirodnih svjetlosnih izvora nikada ne mogu dati koherentnu svjetlost. To će biti lako razumljivo ako se podsjetimo da je svjetlosni talas rezultat kvantnih procesa u atomima od kojih je izvor izgrađen. Zračenje jednog atoma traje oko 10 –8 s. Istovremeno zrači više atoma, a ta zračenja se slažu u jedinstven svjetlosni talas. Svaka druga kombinacija atoma i njihovih reakcija daje drugi svjetlosni talas. Zato je praktično nemoguće dobiti dva stvarna koherentna svjetlosna izvora.
Postoji niz postupaka za umjetno dobivanje koherentnih izvora. Najjednostavniji postupak prikazan je na slici 1.
Koherentni svjetlosni talasi (1) i (2), polazeći od tačkastog izvora S, različitim putevima dolaze na isto mjesto u tačku P. Izgleda kao da je talas (2) došao iz izvora S' koji predstavlja lik izvora S u ogledalu 0.
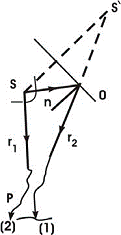
Slika 1. Postupak za dobivanje koherentnih talasa
Neka je geometrijska dužina prijeđenih puteva od izvora
S do tačke P zraka (1) i (2) respektivno r1 i r2 zbog
putne razlike Δr = r2 – r1 zrake stižu u tačku P s izvjesnom
faznom razlikom. U tački P ispunjeni su opšti uslovi za ostvarivanje interferencije:
za Δ= n λ uz n = 0, 1, 2,…, maksimalno pojačanje, a za Δ=(2n+1)λ/2 uz
n=0, 1, 2,…, maksimalno slabljenje osvjetljenja tačke P
Fresnel je predložio da se kao koherentni izvori koriste dva lika jednoga
stvarnoga svjetlosnog izvora dobivena u sva ravna ogledala. Šema Fresnelova
ogleda dana slici 2., gdje su 01 i 02 dva ravna ogledala postavljena pod
uglom ϕ, a S izvor svjetlosti. Likove S1 i S2 svjetlosnog izvora s u ogledalima
01 i 02 dobivamo po pravilu konstrukcije lika zadanog predmeta u ravnom
ogledalu. Ti likovi djeluju kao dva samostalna koherentna svjetlosna izvora
iz kojih se šire dva snopa zraka. Te zrake se susreću i ukrštaju u oblasti
0AB, pa će na tim mjestima doći do njihove interferencije. Ako se izvor
svjetlosti S uzme u obliku uske pukotine, na zaklonu z, kao rezultat interferencije
pojavit će se svijetle i tamne pruge.
Označimo sa d udaljenost izvora S1 i S2 , a njihovu udaljenost
od zaklona sa l (slika 2.)Udaljenost između prvih interferentnih
pruga neka je BB1 = x. Puteve koji zrake prijeđu od izvora S1
i S2 do tačke B obilježimo sa r1 i r2.
Putna razlika Δr = r2 – r1 ovih zraka dobiva
se ako se iz tačke B opiše luk poluprečnika r1, on siječe zraku
S2B u tački N. Putna razlika tih dvaju talasa je Δ = S2N.
Prema tome, u tački B pojavit će se tamna interferentna pruga samo onda
ako je
S2N=![]()
Iz pravouglih trouglova ΔS1BC i ΔS2BD na osnovi Pitagorine teoreme možemo
pisati
r12=l2+( ![]() -
- ![]() )2
)2
r22=l2+( ![]() +
+ ![]() )2
)2
Oduzimanjem tih jednačina i sređivanjem dobiva se
(r1+r2)(r1-r2)=dx
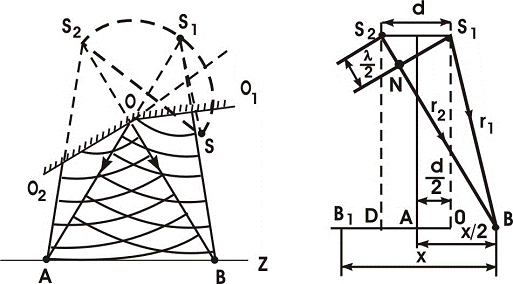
Slika 2. Šema Fresnelova eksperimenta
Kako je udaljenost AB vrlo mala u odnosu na dužinu 1, možemo približno uzeti da je r1 = r2 = 1, što znači da je r1 + r2 = 21, a kako je (r2 – r1) = λ/2, uvrštavanjem tih vrijednosti dobiva se
![]() =
=![]()
Na osnovi poznatih vrijednosti d, l i x može se izračunati talasna dužina za svjetlosne zrake različitih boja.
PRIMJENA INTERFERENCIJE
Interferencija svjetlosti ima važne primjene u nauci i tehnici, kao što je određivanje talasnih dužina svjetlosti, tačno određivanje malih uglova i dužina, ispitivanje kvaliteta obrade površina, određivanje indeksa loma, ispitivanje strukture spektralnih linija i slično. Uređaji, koji rade na principu interferencije koherentne svjetlosti, nazivaju se interferometri. Oni su različitih konstrukcija, prema vrsti namjene.
DIFRAKCIJA SVJETLOSTI
Pojava interferencije svjetlosti poslužila
je kao uvjerljiv dokaz talasne prirodne svjetlosti. Međutim, definitivna
pobjeda talasnih shvatanja bila je nemoguća bez tumačenja fundamentalnog
i pokusno potvrđenog zakona pravolinijskog širenja svjetlosti.
“Huygensov princip” omogućava da se objasne pojave
refleksije i refrakcije svjetlosti, međutim pojavu pravolinijskog širenja
svjetlosti u biti ne rješava jer on nije postavljen u vezi s pojmom
odstupanja od pravolinijkog pravca tj. sa pojavom difrakcije. Huygensov
princip u svom prvobitnom obliku bio je princip čije je područje primjena
bila oblast geometrijske optike. On se odnosio na slučajeve kada su
postojale talasne dužine beskonačno male u odnosu na dimenzije talasne
fronte. Zato je omogućavao da se riješe samo zadaci o pravcu širenja
svjetlosnog talasnog fronta, a nije zalazio u probleme intenziteta talasa
koji se gibaju u raznim pravcima. Taj nedostatak je upotpunio Fresnel
koji je Huygensovom principu dao fizikalni smisao dopunivši ga idejom
o interferenciji talasa. Zahvaljujući tome ovojna površina elementarnih
talasa koju je Huygens uveo čisto formalno dobila je jasan fizikalni
sadržaj kao površina na kojoj, zbog uzajamne interferencije elementarnih
talasa, rezultirajući talas ima znatan intenzitet.
Ako između zastora A i izvora S koji ga osvjetljava, stavimo drugi zastor
B s otvorom na zastoru A će se pojaviti svijetli lik ograničen tamnim
poljem (slika 3)
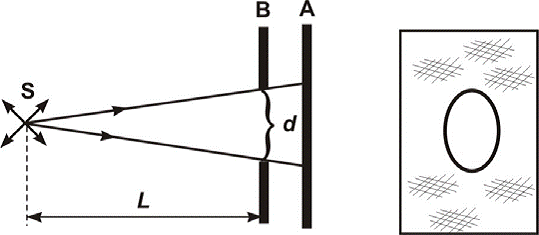
Slika 3. Formiranje lika pomoću zastora
Granicu tamne sjene možemo naći geometrijskim putem pretpostavljajući
da se svjetlost širi pravolinijski. Međutim, tačnijim promatranjem pokazuje
se da tamna granica nije oštra što je naročito primjeti u slučaju d<<L.
Tada je zapravo svijetli lik na ekranu A omeđen svijetlim i tamnim krugovima
koji postepeno prelaze jedni u druge. To govori da se svjetlost ne širi
pravolinijski već ogiblje otvor B. Opisana pojava nepravolinijskog širenja
svjetlosti naziva se difrakcija.
Pojava difrakcije talasa je jako izražena na preprekama (otvorima) koje
su reda veličine njihove talasne dužine. Kako je talasna dužina svjetlosti
vrlo mala (reda veličine 10 – 7m) to se za pojavu difrakcije svjetlosnih
talasa moraju ostvarivati posebni uslovi.

Slika 4. Pojava difrakcije
Razlikuju se dva slučaja:
1. Fresnelova difrakcija – kada se svjetlosni izvor i prepreka
(otvor), na kojoj se obavlja difrakcija, nalaze na konačnoj udaljenosti
2. Fraunhoferova difrakcija (difrakcija paralelnih svjetlosnih
talasa) – kada svjetlosni talasi dolaze od beskonačno udaljenih svjetlosnih
izvora do prepreke (otvora) na kojoj se obavlja difrakcija.
FRESNELOVA DIFRAKCIJA
Huygensov princip pomoću kojega smo objasnili pojavu difrakcije ne daje
nikakvu informaciju o promjeni amplitude svjetlosnih talasa koji se iza
prepreke (otvora) šire u svim pravcima. Fresnel je dopunio Huygensov princip
teorijom o interferenciji sekundarnih svjetlosnih talasa nastalih kao
rezultat difrakcije. Poznavanjem amplitude i faza sekundarnih svjetlosnih
talasa može se naći amplituda rezultujućeg talasa u bilo kojoj tački prostora
iza prepreke. S pomoću tako proširenog gledišta, Huygens-Fresnelovog principa,
Fresnel je uspio objasniti čitav niz difrakcijskih pojava i pokazati kako
je talasna priroda svjetlosti u saglasnosti sa eksperimentom uočenim pravolinijskim
širenjem svjetlosti.
Postupak primjene Huygens-Fresnelovog principa dobio je naziv metoda Fresnelovih
zona.
DIFRAKCIJA NA KRUŽNOM OTVORU
Ako na put sfernom svjetlosnom talasu postavimo pregradu s kružnim otvorom (sl.5.), na ravnom zaklonu koji je paralelan pregradi pojavit će se difrakcijska slika sa svijetlim i tamnim poljima, koja će se naizmjenično smjenjivati.
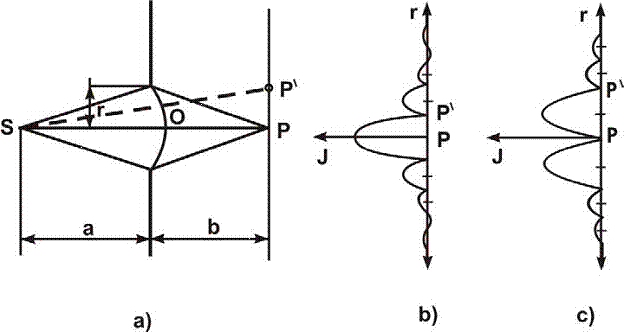
Slika 5. Difrakcija na kružnom otvoru
U tački P će se smjenjivati svjetla (slika 5,b) i tamna (slika 5,c) polja ovisno o tome kojem broju (neparnom ili parnom) Fresnelovih zona odgovara otvor na pukotini. Na primjer, ako je otvor veličine prve Fresnelove zone, dobit ćemo difrakcijsku sliku prikazanu na slici 5,b, ako se poveća na veličinu dviju Fresnelovih zona dobit ćemo difrakcijsku sliku prikazanu slikom 5,c. Na taj način difrakcijska slika kružnog otvora predstavlja svijetle i tamne koncentrične prstenove naizmjenično posložene u odnosu na centralnu svijetlu ili tamnu kružnu površinu, što ovisi o veličini otvora.
POLARIZACIJA SVJETLOSTI
Dosadašnja razmatranja provedena su pod pretpostavkom da svjetlost ne
pokazuje nikakva orijentirana svojstva u prostoru.
Transverzalna priroda svjetlosti (elektromagnetnih talasa) omogućava njenu
poprečnu orijentaciju. Zraka prirodne svjetlosti sastavljena je od titranja
svjetlosnog vektora što se vrše u svim pravcima normalno na pravac širenja
svjetlosti (sl.6).
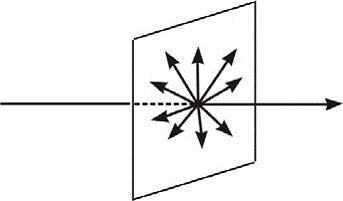
Slika 6. Svjetlosna zraka
To je uslovilo činjenicom da zraka prirodne svjetlosti nastaje od velikog broja talasnih nizova, paketa, koje ispuštaju pojedini atomi.
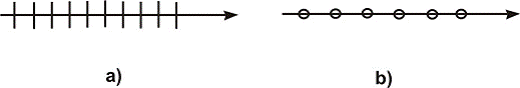
Slika 7. Šematski prikaz polarizovanih zraka
Ravan titranja za svaki talasni niz orijentisana je na slučajan način. Zato su u rezultirajućem talasu titranja različitih smjerova jednako vjerovatne. Svjetlost kod koje se titranja svjetlosnih vektora događa samo u jednom pravcu, također normalnom na pravac širenja, naziva se POLARIZOVANOM. Ravan u kojoj titra svjetlosni vektor nazvati ćemo ravan titranja. Polarizovana svjetlosna zraka šematski se predstavlja crtežom (sl. 7,a) ako ravan svjetlosnog vektora leži u ravni crteža, a crtežom (sl. 7,b) ako je normalna na ravan crteža.
Polarizacija se može pojaviti pri refleksiji, refrakciji, pri dvojnom prelamanju i s pomoću selektivne apsorpcije.
FOTOELEKTRICNI EFEKAT
Među pojave u kojima se ispoljavaju korpuskularne osobine svetlosti dolazi u prvom redu oslobađanje elektrona dejstvom svetlosti – fotoelektrični efekat.
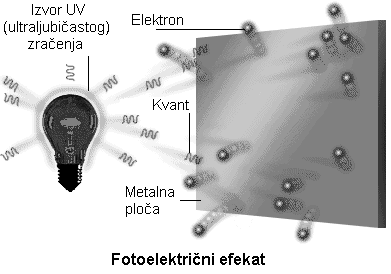
Ova pojava se sastoji u udaljavanju negativnog elektriciteta
sa površine metala pod dejstvom ultravioletne svetlosti.
Dalja istraživanja su pokazala da se suština fotoelektričnog efekta sastoji
u oslobađanju elektrona.
Lenard je 1899. god. ustanovio da se ovaj efekat zasniva na emisiji elektrona
iz metalne elektrode kada na ovu padne svetlost kraće talasne dužine.
Ovakva pojava – da se dejstvom svetlosti mogu osloboditi elektroni iz
metala – nazvana je f o t o e l e k t r i č n i e f e k a t.
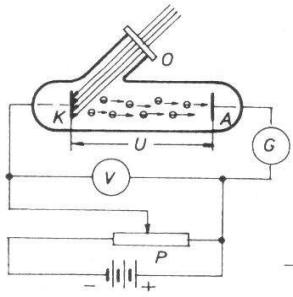
Aparatura za ispitivanje fotoefekta
Intenzitet struje je jednak nuli tek kada se na anodu stavi negativan napon- napon zaustavljanja Ucn.
Pri smanjenju negativnog i povećanju pozitivnog napona intenzitet struje kroz cev raste samo do jedne granice odnosno do struje zasićenja.
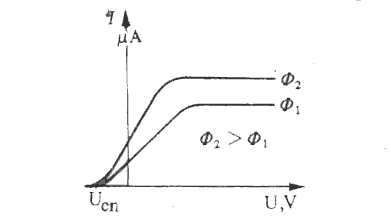
Grafik intenziteta struje u funkciji od napona
Lenard je 1902. god. došao do eksperimentalnih rezultata koji su odigrali odlučujuću ulogu u razvoju shvatanja prirode svetlosti. Ovi rezultati se mogu prikazati sa tri važna stava:
- Maksimalna kinetička energija elektrona koje oslobađa svetlost iz metala nezavisna je od intenziteta svetlosti i zavisi samo od talasne dužine svetlosti.
- Kinetička energija fotoelektrona je proporcionalna frekvenciji svetlosti koja izaziva fotoefekat.
- Fotoelektrični efekat počinje tek kada talasna dužina upotrebljene svetlosti bude manja od jedne određene talasne dužine , koja se naziva granična talasna dužina.
Kasnije je ustanovljen i sledeći stav:
- Fotoefekat nastupa uvek u nemerljivo kratkom vremenu posle početka dejstva svetlosti.
Sve do granične frekvencije Vg ne dolazi do fotoelektričnog
efekta.
Granična frekvencija zavisi od vrste metala. Najmanje granične frekvencije
imaju alkalni metali.
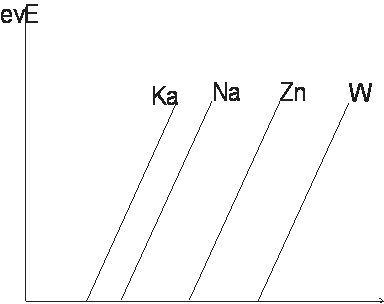
Grafik zavisnosti energije elektrona od frekvencije svetlosti za različite
metale
PRIMJENA FOTOELEKTRICNOG EFEKTA
Primena fotoefekta se obično vrši pomoću f o t o ć e l i j a.
Fotoćelije obično služe za prevođenje promena svetlosnog fluksa u promene intenziteta električne struje.
Fotoelektrični efekat može da se vrši na dva načina:
- kad elektroni prime dovoljno energije da mogu da izlete iz tela u spoljašnji prostor - spoljašnji fotoelektrični efekat .
- primljena energija je nedovoljna da elektroni napuste telo, ali ta energija eksituje elektrone - unutrašnji fotoelektrični efekat .
Spoljašnji
fotoelektricni efekat
Za praktičnu upotrebu fotoefekta značajna je pojava tzv. fotoelektričnog
zamora. Primećeno je da se emisija fotoelektrona sa površine metala smanjuje
sa vremenom.
Unutrašnji fotoelektricni efekat
Za praktične ciljeve mnogo je važniji unutrašnji fotoefekat na poluprovodnicima.
I kada su poluprovodnici neosvjetljeni, kroz njih protiče izvesna struja,
tzv. tamna struja. Pri osvetljenju poluprovodnika nastupa unutrašnji fotoelektrični
efekat i struja u kolu se poveća.
U grupi fotoćelija sa unutrašnjim fotoefektom razlikuju se dva tipa:
a) Fotoćelije sa zaprečnim slojem (fotoelementi),
b) Fotootpornici.
Kod fotoelemenata se svetlosna energija prevodi u rad
električne struje, pa se može reći da je ovo neka vrsta elemenata slična
galvanskim
Fotootpornici su fotoćelije čije se dejstvo zasniva na
promeni otpornosti poluprovodnika pod dejstvom svetlosti. To je pločica
od izolatora na kojoj je nanešen tanak sloj nekog poluprovodnika.
Postoji još jedna vrsta fotoćelija koja je u današnje vreme našla najveću
primenu u ljudskom životu i naziva se solarna ćelija.
Solarna ćelija predstavlja element električnog kola koji vrši konverziju
energije sunčevog zračenja u električnu energiju.
KOMPTONOV EFEKAT
Proučavajući rasturanja X-zraka, dobijenih iz rentgenske cijevi, pri
nailasku na grafit ili neko drugo podesno čvrsto tijelo, američki fizičar
Kompton (A. H. Compton) 1923.godine utvrdio je da se među rasturenim zracima
pored onih, koji ostaju bez promjene svoje talasne dužine, nalaze i takvi
zraci, kojima su se talasne dužine povećale u poređenju
sa duzinom upadnih zraka.
Ova pojava, da kod X-zraka, koji se rasturaju pri prolazu kroz čvrste
materije,nastaje povećanje njihove talasne dužine, poznato je pod imenom
Komptonov efekat.Kompton je 1927.godine dobio Nobelovu
nagradu zajedno sa Vilsonom.
Analizu rasturenih X-zraka Kompton je vršio pomoću spektrografa za X-zrake,
a spektralnu raspodjelu njihove intenzivnosti mjerio je pomoću jonizacione
komore.
Povećanje talasne duzine pri Komptonovom efektu, tj. pojava povećanja
talasne dužine X-zraka pri njihovom rasturanju kroz datu materiju već
u pocetku je razmatrano kao rezultat uzajamnog dejstva fotona sa jednim
od elektrona u atomima materije na kojoj se vršilo njihovo rasturanje.
Razlog ovom shvatanju je proizašao na osnovu eksperimentalno utvrđenih
činjenica.Naime prema fotografskim snimcima spektara rasturenih zraka
izlazi da povećanje njihove talasne dužine ne zavisi od talasne dužine
primarnih zraka i prirode materije koja vrši rasturanje, nego samo od
ugla rasturanja ![]() ,
i to tako, da raste sa uvećanjem ovog ugla. Isto tako, utvrđeno je da
intenzivnost promjene linije u spektru raste sa uvećanjem ugla rasturanja.
,
i to tako, da raste sa uvećanjem ovog ugla. Isto tako, utvrđeno je da
intenzivnost promjene linije u spektru raste sa uvećanjem ugla rasturanja.
Da proces Komptonovog efekta nastaje pri sudaru fotona sa jednim elektronom
na koji nailazi, očevidno je dokazano posmatranjem ove pojave u Vilsonovoj
komori. Naime, tragovi elektrona velike brzine, koje izbacuju X-zraci
iz atoma date materije, ovdje se vide. Na osnovu veličine radijusa krivine
putanja ovih tzv. odskočnih ili Komptonovih elektrona
u magnetnom polju određuje se veličina njihove energije.
Treba imati u vidu da je Komptonov efekt najizrazitiji kod ![]() -zraka
i tvrdih rentgenskih zraka.
-zraka
i tvrdih rentgenskih zraka.
Prema teoriji Komptona, a istovremeno i Debaja (Debye), Komptonov efekt
može se ovako objasniti:
Na osnovu pretpostavke da se X, odnosno ![]() -zraci
sastoje iz fotona, koji imaju određenu količinu energije E=hv, pri čemu
je h Plankova konstanta a v frekvencija upadnih zraka, i da imaju određenu
količinu kretanja, izlazi da pri sudaru fotona sa elektronom mora nastati
rasturanje fotona i odskok elektrona istovremeno, kao da su se sudarile
dvije elastične kuglice.
-zraci
sastoje iz fotona, koji imaju određenu količinu energije E=hv, pri čemu
je h Plankova konstanta a v frekvencija upadnih zraka, i da imaju određenu
količinu kretanja, izlazi da pri sudaru fotona sa elektronom mora nastati
rasturanje fotona i odskok elektrona istovremeno, kao da su se sudarile
dvije elastične kuglice.
Pri direktnom sudaru, foton X-zraka ili ![]() -zraka,
odbije se od elektrona u položaju S i skrene za ugao
-zraka,
odbije se od elektrona u položaju S i skrene za ugao ![]() (ugao rasturanja) od prvobitnog pravca FS.
(ugao rasturanja) od prvobitnog pravca FS.
Pošto foton pri sudaru jedan deo svoje energije prenese na elektron, njegova
energija će se smanjiti na E1=hv1. Prema tome, s obzirom da je E1<E
odnosno hv1< hv biće v1 < v. Uslijed promijene frekvencije, mijenja
sa i talasna dužina fotona.
Kako je talasna dužina fotona prije sudara ![]() =
=![]() , a poslije sudara
, a poslije sudara ![]() 1=
1=![]() gdje je c brzina svjetlosti u vakumu, na osnovu nejednačine v1 < v
izlazi 𝛌1 > 𝛌, tj. talasna dužina poslije sudara se
povećava, što je eksperimentalno bilo utvrđeno.
gdje je c brzina svjetlosti u vakumu, na osnovu nejednačine v1 < v
izlazi 𝛌1 > 𝛌, tj. talasna dužina poslije sudara se
povećava, što je eksperimentalno bilo utvrđeno.
Na osnovu ove teorije, da se Komptonovo rasturanje fotona na slobodnom
elektronu može tretirati kao sudar elastičnih kuglica , izlazi, da u tom
slučaju važi zakon održanja energije i impulsa, kako za fotone, tako i
za elektrone. Primjenom ova dva zakona može se matematičkim putem naći
zavisnost promjene talasne dužine upadne svjetlosti od ugla rasturanja
kod Komptonovog efekta.
Imajući u vidu da je energija fotona prije sudara sa elektronom iznosila
hv, a poslije sudara hv1, i da je energija elektrona, data u relativističkom
izrazu, prije sudara iznosila moc2 a poslije sudara sa fotonom mc2, gdje
je mo-masa elektrona u mirovanju, a m njegova masa, kada sa kreće brzinom
v, tj. m=![]() , onda u slučaju sudara fotona sa elektronom, primjenom zakona održanja
energije slijedi jednačina hv+moc2=hv1+mc2 , ili mc2=h(v-v1)+moc2
, onda u slučaju sudara fotona sa elektronom, primjenom zakona održanja
energije slijedi jednačina hv+moc2=hv1+mc2 , ili mc2=h(v-v1)+moc2
Na osnovu izloženog možemo zaključiti da je Komptonov efekt jedan od najubjedljivijih
dokaza postojanja fotona, odnosno korpuskularnih osobina svjetlosti.
preuzmi
seminarski rad u wordu » » »
