Gasno stanje materije

Gasno stanje materije je za hemiju od velike važnosti pa se stoga osobine gasova izučavaju i u hemiji. Izučavanjem osobina gasova došlo se do razlikovanja atoma i molekula. Za gasove jhe karakteristično,za razliku od čvrstih i tečnih supstancija da postoji određen odnos između gustine razređenih gasova i molekulskih težina. U hemiji je taj odnos iskorišćen za izračunavanje atomskih težina, zatim za određivanje gasnih gustina supstancija čiji je molekulski satav poznat,ili za određivanje molekulskih težina gasova iz njihovih gustina kod gasova čiji je molekulski sastav nepoznat. Gasni zakoni se primenjuju i u kvantitativnoj analizi.
Za biologiju i medicinu je poznavanje osobina gasova od velike važnosti, jer su mnogi žiovotni procesi u vezi sa razmenom gasova (kiseonik prilikom disanja, ugljen-dioksid prilikom hlorofilne asimilacije i drugo).
Od svih stanja materije gasno je najjednostavnije. Gasovi se upadljivo razlikuju od tečnosti i čvrstih supstancija osobinom da je njihova zapremina u velikoj meri zavisna od pritiska i temperature. Zapremina određene količine tečnosti se neznatno menja pri promeni pritiska i temperature. Povećanjem pritiska od 1 na 2 atmosfere zapremina vode se smanjuje za 0,01 % a povišavanjem temperature od 0 do 100 C zapremina vazduha se znatno povećava, i to oko 36,6 stepeni. Dakle, promenama pritiska i temperature zapremina gasova se mnogo menja, i to nezavisno od prirode gasa.

Gasovi su ekspanzivni, tj. sposobni da zauzmu zapreminu koja im se stavi na raspolaganje, gasovi se mogu lako kompromitovati, oni imaju malu gustinu i neznatan viskozitet.
Zapremina gasa je određena kada su poznati uslovi pod kojima se on nalazi. Ti uslovi su temperatura i pritisak. Prema tome, stanje gasa karakterišu tri osnovne veličine: temperatura, pritisak i zapremina. Arbitarno je usvojeno da se temperatura od 0̊ C i pritisak od 1 atmosfere smatraju kao normalni uslovi. Kod gasova se najčešće upotrebljava kao jedinica za pritisak 1 atmosfera.
Kada se primenom jednačine gasnog stanja, kod jednog gasa koji nije pod normalnim uslovima, izračuna njegova zapremina pod normalnim uslovima, kaže se da je zapremina gasa redukovana na normalne uslove.

Kako se mere gasovi? Čvrste supstancije se mogu lako meriti na vagi. Tečne supstancije se mogu meriti na vagi ili preko zapremine doći do težine ako se zapremina odgovarajuće tečnosti pomnoži sa njenom specifičnom težinom. Merenje gasa na vagi nije jednostavno, s jedne strane, zato što gasovi imaju male specifične težine, a s druge strane, zato što je određivanje specifičnih težina gasova dosta komplikovano. Mnogo je jednostavnije iz zapremine gasa pod određenim uslovima izračunati težinu gasa. I ovo je jedan od razloga zbog kojih se gasno stanje materije izučava i u hemiji. Gasni zakoni se odnose na tzv. idealne gasove, a obični ili realni gasovi dosta približno slede gasne zakone. Pri visokim pritiscima ili niskim temperaturama kod realnih gasova gasni zakoni se ne mogu primenjivati.
Gasovi su korpuskularne prirode, sastavljeni iz molekula koji se slobodno kreću u prostoru. Gasni molekuli, praktično uzevši, međusobno se ne privlače nego se slobodno kreću u zapremini koja je znatno veća od stvarne zapremine gasnih molekula. Vandervalsove (Van der Waals) sile međusobnog privlačenja molekula kod razređenih gasova se mogu zanemariti jer su gasni molekuli udaljeni jedni od drugih. Međutim, kod komprimovanih gasova molekuli su veoma bliski jedni drugima i oni se privlače. Zbog slobodnog kretanja gasnih molekula gasovi nemaju ni stalanoblik ni stalnu zapreminu. Udaranjem gasnih molekula o zidove suda objašnjava se gasni pritisak. Mogućnost ekspanzije i kompresije gasova se objašnjava promenom međumolekulskog prostora. Kod idealnih gasova ne bi postojalo privlačenje među molekulima.

Kod razređenih gasova stvarna zapremina gasnih molekula je vrlo mala i predstavlja jedva hiljaditi deo zapremine suda u kome se gas nalazi. Ovo se može sledećim primerom ilustrovati. Ako se izmeri 1g joda, ćija je zapremina u čvrstom stanju 0,2 ml, pa se ista količona čvrstog joda prevede u stanju pare, njegova zapremina pri 1 atmosferi i 184 C iznosiće 148 ml, tj biće oko 700 puta veća nego u čvrstom stanju.

VARIJACIJA GASNE ZAPREMINE SA PRITISKOM BOJL-MARIOTOV ZAKON

Bojl i Mariot otkrili su nezavisno jedan od drugoga zakon koji glasi: pri stalnoj temperaturi postoji između pritiska i zapremine određene mase gasa obrnut odnos. Povećanjem zapremine opada pritisak i obratno. Ako se zapremina, na primer, dva puta poveća, pritisak će se dva puta smanjiti itd. Ako se pritisak gasa označi sa P, a zapremina sa V, dobija se sledeći obrazac:
P*V=K (temperatura je stalna)

Prema tome, Bojl-Mariotov zakon se može ovako definisati: proizvod pritiska i zapremine određene mase nekog gasa pri stalnoj temperaturi je uvek isti, ili zapremina nekog gasa pri stalnoj temperaturi je obrnuto proporcionalna pritisku.

Pritisak je definisan kao sila na jedinicu površine. Jedinica za pritisak je atmosfera. Atmosferom se naziva onaj pritisak koji vrši stub vazduha. Tom pritisku drži ravnotežu stub metalne žive visok 76cm ili 760mm. Ako se napuni staklena cev (mora biti duža od 76cm) živom, zapuši i obrnuta cev sa otvorom postavljenim naniže uroni u živu i otpuši otvor, živin stub u cevi će se spustiti tako da će visina stuba iznositi 760mm(slika 1). Pritisak vazdušnog stuba jednak je pritisku živinog stuba cevi.

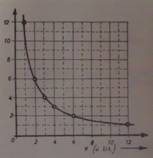
Slika 1. – Toričelijev ogled Grafik 1. – Grafički prikaz Bojl-Marijotovog zakona

Bojl Marijotov zakon se može primeniti samo na razređene gasove. Pri velikim pritiscima ili pri niskim temperaturama Bojl-Mariotov zakon pokazuje primetna odstupanja. Za većinu gasove se može reći da je pri visokim pritiscima nađena zapremina gasa uvek veća od teorijske zapremine, tj. od one zapremine koja se dobija Bojl-Mariotovom zakonu.

VARIJACIJE GASNE ZAPREMINE ILI PRITISKA SA TEMPERATUROM

-Šarlov ili Gej Lisakov zakon-

Ovaj zakon je otkriven oko sto godina posle Bojl-Mariotovog. Francuski fizičar Šarl utvrdio je 1787. god da se različiti gasovi pri zagrevanju ravnomerno šire, a francuski fizičar Gej-Lisak odredio je 1802. god koeficijent širenja gasova, koji se označava sa α i iznosi

. On je isti za različite gasove.

Zagrevanjem određene mase nekog gasa pri stalnom pritisku povećava se zapremina bez obzira na njegovu hemijsku prirodu. Ako se gas nalazi na 0° C pa se zagreje na 1° C, zapremina će se uvećati za

deo one zapremine koju je gas imao pri 0° C. Ako se zapremina gasa na 0° C označi sa V0, a zapremina na 1° C sa V1, onda će biti:

Sa t ozbačavamo temperaturu u stepenima Celzijusove skale. Gej-Lisakov zakon se može ovako definisati: zapremina određene mase nekog gasa pri stalnom pritisku povećava sde za svaki stepen Celzijusov za

deo od one zapremine koju je gas imao pri 0° C.

Ako se jedan gas pri zagrevanju raspada, broj molekula će se povećavati pa će se stoga i pritisak menjati, tj. povećavati. U takvim slučajevima Gej-Lisakov se zakon ne može primeniti. Prema tome Gej-Lisakov zakon se može primeniti samo ako je pritisak i broj molekula jednog gasa konstantan.

Zagrevanjem određene mase gasa pri stalnoj zapremini povećava se pritisak gasa za

deo onog pritiska koji je gas imao pri 0̊ C:

Pt = P0 +

* t = P0 (1 + αt)

Pt je pritisak gasa na temperaturi t ° ; P0 je pritisak gasa na 0° a α je koeficijent širenja gasova.

Na temperaturi -273° C pritisak bi trebalo da bude ravan nuli. Međutim, do toga ne dolazi, jer se gas veća iznad te temperature pretvara u tečno stanje. Na temperaturi 273° C pritisak se udvostručio u odnosu na pritisak koji je vladao pri 0° C.
Odnos temperature i gasnog pritiska pri stalnoj zapremini kože se predstaviti grafički slično kao i Gej-Lisakov zakon pri stalnom pritisku.

JEDNAČINA GASNOG STANJA ILI KLAJPERONOVA JEDNAČINA

U jednačini gasnog stanja su povezani Bojl-Mariotov i Gej-Lisakov zakon. Bojl-Mariotov zakon se predstavlja sa P*V=K pri stalnoj temperaturi, a Gej-Lisakov zakon sa Vt=V0(1+αt) pri stalnom pritisku.

Ako se uzme da je zapremina određene mase nekog gasa V0 (pri 0°), pa se gas pri stalnom pritisku zagreje na t stepeni, zapremina će se po Gej-Lisakovom zakonu povećati.

Gram-molekul je ona količina neke supstancije čija težina iznosi onoliko grama kolika je molekulska težina pomenute supstancije. Molekulska težina je broj koji pokazuje koliko je molekul jedne supstancije teži od jednog atoma vodonika ili, tačnije, koliko je puta teži od

atoma ugljenika. Nađeno je da svaki gram-molekul gasa pod normalnim uslovima zauzima zapreminu od 22,41 litra. Zapremina 22,41 litra naziva se molekulskom zapreminom gasa.

Jednačina gasnog stanja obično služi za izračunavanje zapremine gasova pod normalnim uslovima, tj. za redukovanje gasnih zapremina. Iz jednačine gasnog stanja dobija se

P-pritisak
V-zapremina
n-broj molova
R-univerzalna gasna konstanta
T-temperatura

VANDERVALSOVA JEDNAČINA

P-pritisak gasa
n-broj molova gasa
T-apsolutna temperatura
V-zapremina gasa
R-univerzalna gasna konstanta
a i b-empirijske konstante

Ranije je već pomenuto da se gasni zakoni koji vrede za idealne gasove mogu primeniti i na realne gasove samo kada su razređeni, tj. kada su pod malim pritiscima i na višim temperaturama. Holandski fizičar Vandervals je, vodeći računa o mogućnostima primene gasnih zakona pri kritičkim pojavama i kondenzovanju gasova, modifikovao jednačinu gasnog stanja unoseći korekture koje se odnose na pritisak i zapreminu.

Gasni pritisak potiče od broja udara gasnih molekula o zidove suda. Molekuli istog gasa imaju različite brzine kretanja, ali se može pretpostaviti da svi molekuli jednog gasa imaju istu sreednju brzinu kretanja. Povećavanjem brzine kretanja gasnih molekula raste, a smanjivanjem brzine kretanja opada gasni pritisak. Molekuli idealnih gasova se ne privlače, a molekuli realnih gasova se više ili manje privlače. Usled međusobnog privlačenja molekula realnih gasova njihove brzine kretanja postaju manje pa je i pritisak manji od pritiska koji bi odgovarao idealnim gasovima (teorijski pritisak), i to za onoliko manji koliko iznosi privlačenje gasnih molekula. Vandervals je eksperimentalno odredio tu razliku i nazvao je kohezioni pritisak. Ako se eksperimentalno određenom pritisku realnih gasova doda kohezioni pritisak, dobija se teorijski pritisak koji odgovara idealnom gasu. Kohezioni pritisak se izražava sa

. U izrazu kohezionog pritiska, a je koeficijent privlačenja koji zavisi od prirode gasa, a V je zapremina suda u kome se nalazi gas. Ukoliko je gas razređeniji, odnosno zapremina gasa veća, kohezioni pritisak je manji. Kod razređenih gasova je kohezioni pritisak toliko mali da se, praktično uzevši, može zanemariti. Međutim, kod komprimovanih gasova i pri nižim temperaturama korektura za pritisak se mora uzeti u obzir. Stoga se u jednačinu gasnog stanja umesto pritiska stavlja P +

Pod zapreminom gasa se podrazumeva slobodan prostor u kome se gasni molekuli kreću. Kod realnih gasova to je međumolekulski prostor, a kod idealnih gasova to je u stvari zapremina suda u kome se gas nalazi, jer molekuli idealnih gasova nemaju zapreminu i mogu se smatrati kao tačke.

DALTONOV ZAKON PARCIJALNIH PRITISAKA

U gasnim smešama svaki gas se ponaša nezavisno od ponašanja ostalih gasova koji ulaze u sastav smeše. Dalton(1807) je dokazao da je celokupni pritisak jedne gasne smeše jednak zbiru parcijalnih pritisaka gasova koji se nalaze u smeši. Ovaj je zakon poznat pod imenom Daltonov zakon parcijalnih pritisaka. Parcijalnim pritiskom naziva se pritisak koji vrši svaki gas iz smeše, a isti bi pritisak vršio i kada bi se sam nalazio u zapremini koju zauzima smeša. Ako se celokupni pritisak gasne smeše označi sa P, a parcijalni pritisci pojedinih gasova sa P1, P2, P3... Pk, Daltonov zakon se može ovako predstaviti:

Dakle, svaki gas u gasnoj smeši vrši jedan deo od celokupnog pritiska, i to srazmerno broju molekula koji se nalazi u datoj zapremini gasne smeše. Pritisak svakog pojedinog gasa jeste parcijalni pritisak.

Daltonov zakon se može primeniti sani pod uslovom da se molekuli različitih gasova smeše međusobno ne privlače i da međusobno hemijski ne reaguju. Prema tome, Daltonov zakon se može preciznije ovako definisati: u smeši gasova koji međusobno ne reaguju hemijskim putem, celokupan pritisak gasne smeše je ravan zbiru parcijalnih pritisaka, ili svaki gas vrši isti pritisak kao kada bi se sam nalazio u istoj zapremini u kojoj se nalazi gasna smeša.

Naročito često se primenjuje Daltonov zakon kada se gasovi nerastvorljivi u vodi hvataju iznad vode u cilju određivanja količine dotičnog gasa. Pritisak nekog gasa koji se nalazi iznad vode jeste, u stvari, pritisak gasa i vodene pare zajedno. Dakle, izmereni pritisak je uvek veći od pritiska samog gasa. Da bi se dobio pritisak samog gasa P, potrebno je od izmerenog pritiska, koji dolazi od gasa i zasićene vodene pare a označava se sa Pg, oduzeti napon zasićene vodene pare na određenoj temperaturi(Pw), dakle P = Pg – Pw. Pritisak zasićene vodene pare zavisi od temperature.

AVOGADROV ZAKON

Avogadrov zakon je jedan od gasnih zakona. Nazvan je prema Amadeu Avogadru koji je 1811. godine izneo pretpostavku da se u jednakim volumenima svih gasova pri istim uslovima temperature i pritiska nalazi jednak broj čestica.

U jednakim zapreminama različitih gasova na istoj temperaturi i pritisku nalazi se jednak broj molekula.

Ovaj se zakon objašnjava činjenicom da je srednja kinetička energija na određenoj temperaturi ista za sve gasove.

Na primeru kinetičke teorije gasova može se lepo videti kako se postavlja jedna teorija i kako se eksperimentalnim činjenicama potvrđuje teorija.Ako se u jedan sud stave dva različita gasa koji imaju molecule istih težina, srednja kinetička energija po molekulu, čak ako je na početku različita, mora kao rezultat sudara na kraju postati ista. Pošto je razmena energije kod elastičnog dudara zavisna od mase I brzine čestica koje se sudaraju, ali nezavisna od njihove prirode, između molekula u smeši ne postoji kinetička razlika pa je srednja kinetička energija molekula prvog gasa jednaka srednjoj kinetičkoj energiji molekula drugog gasa. Stoga se pri istoj temperature može uzeti da je srednja kinetička energija po molekulu za dva gasa koji imaju molecule istih težina konstantna. Maksvel je pokazao da se ovo važno pravilo može primeniti na sve molecule nezavisno od njihove mase. Stvarni dokaz zasniva se na zakonu raspodele brzine, ali je suviše složen da bi se ovde pokazao.

KINETIČKA TEORIJA GASOVA

Materija u gasovitom stanju homogeno zauzima svaki prostor u kome se nalazi. U svakom delu zapremine suda gasna gustina biće ista. Jedino u visokim stubovima gasova, kao na primer, kod vazdušnog stuba, igraće Zemljina teža izvesnu ulogu, a gustina će biti veća u donjim slojevima.

Gasovi nemaju ni stalan oblik ni stalnu zapreminu, već zauzimaju zapreminu suda u kome se nalaze.Tečnosti nemaju određen oblik, ali pri određenoj temperaturi imaju određenu zapreminu.Tečnosti imaju oblik suda u kome se nalaze.Čvrsta tela imaju određen oblik i zapreminu.

Gas difunduje u sudu iako se u njemu već nalazi neki gas. Ova činjenica je važna za poznavanje prirode gasa.Najlakše je pretpostaviti da gasovi prolaze jedini kroz druge zato što imaju zrnastu strukturu koja omogućava prolaz čestice jednog gasa između čestica drugog gasa, i obrnuto. Te sićušne čestice materije zovu se molekuli, a među njima je prazan prostor (intermolekulski prostor). Kroz ovaj međumolekulski prostor prolaze gasovi kao kroz filtar. Stišljivost gasova se objašnjava smanjivanjem ovog prostora a ekspanzivnost njegovim povećanjem.Dolazi se do zakljucka da gasni molekuli zauzimaju srazmerno mali deo zapremine suda, dok je veći dep zašremine suda tzv. međumolekulski prostor. Stvarna zapremina gasnih molekula je

deo zapremine gasa pod normalnim uslovima. Gasni molekuli se mogu kompresijom međusobno jako približiti (smanjivanjem zapremine gasa), tako da bi se moglo reći da se molekuli skoro dodiruju.

Dufuzija gasova je jedna od potvrda molekulske teorije. Ona se može objasniti neprekidnim kretanjem gasnih molekula. Difuzija ide mnogo lakše u vakuumu, a teže u sudu u kome se već nalazi neki gas. Sporija difuzija kroz gasove ne objašnjava se manjom brzinom kretanja gasnih molekula, već sudaranjem sa gasnim molekulima postojećeg gasa. Ovim sudarima molekuli koji difunduju vračaju se i treba im više vremena da pređu određen put nego kada bi se nalazili u vakuumu. Ako u cilindru u kome je vakuum razbijemo cevčicu u kojoj je brom, cilindar će se mnogo brže obojiti bromom nego ako se taj ogled izvrši u cilindru u kome je vazduh.

Pritisak gasa se može objasniti kretanjem gasnih molekula. Udarom molekula o zidove suda nastaje gasni pritisak koji je proporcionalan broju molekula u jedinici zapremine.

Gasni molekuli se kreću pravolinijski velikim brzinama. Pri kretanju se međusobno sudaraju, a udaraju i o zidove suda u kome se nalaze. Usled međusobnog sudaranja i udaranja o zidove suda molekuli stalno menjaju pravac kretanja.

Sudari moraju biti elastični jer pri sudaranju ne dolazi do promene ukupne kinetičke energije gasnih molekula. Kada bi se brzina pri sudaranju gasnih molekula smanjivala, dolazilo bi do smanjivanja pritiska, a to nije slučaj.

U svakom gasu pojedini se molekuli na jednoj određenoj temperaturi kreću različitim brzinama i imaju različite kinetičke energije. Metodama statističke mehanike je utvrđeno da je srednja kinetička energija ista za različite gasove na istoj temperaturi i da raste proporcionalno temperaturi. Srednje kvadratne brzine su različite za razne gasove. Srednja kvadratna brzina molekula vodonika na 0° C iznosi 1,84

, a na 820° C iznosi 3,68

. Pošto je srednja kinetička energija molekula ista za različite gasove, izlazi da su srednje kvadratne brzine obrnuto proporcijalne kvadratnom korenu njihovih molekulskih težina. Pošto je molekulska težina kiseonika šesnaest puta veća od molekulske težine vodonika, molekuli kiseonika kretaće se tačno četiri puta sporije od molekula vodonika, tj. srednja kvadratna brzina kiseonika pri 0° C iznosiće 0,46

Izučavanjem fizičkih i hemijskih osobina materije dolazi se do zaključka da materija nije kontinuirana, već je sastavljena iz sitnih čestica, nazvanih molekuli. Ovako formulisana teorija je poznata pod imenom molekulska teorija.

Navodimo nekoliko primera kako se mogu pojedini gasni zakoni objasniti kinetičkom teorijom gasova:

Smanjivanjem zapremine gasa pritisak se povećavam, jer se povećava i broj udara gasnih molekula na jediničnu površinu u jedinici vremena. Obrtno se događa pri povećavanju zapremine.

Pri stalnoj zapremini pritisak nekog gasa pri zagrevanju raste iako je broj molekula ostao isti. U zagrejanom gasu pritisak postaje veći zato što se zagrevanjem povećava brzina gasnih molekula.

Ovaj takon se objašnjava činjenicom da je srednja kinetička energija na određenoj temperaturi ista za sve gasove

Na primeru kinetičke teorije gasova može se lepo videti kako se postavlja jedna teorija i kako se eksperimentalnim činjenicama potvrđuje teorija. Navešćemo sumaran pregled važnijih postavki kinetičke teorije, a zatim eksperimentalne potvrde tih postavki.

Gas nema stalan oblik ni zapreminu jer se slobodno kreće, a molekuli teže da ispune prostor koji im je dostupan. Najveći deo zapremine gasa je slobodan prostor i zato gasovi imaju malo gustinu i veliku stišljivost. Prema tome gasovi su zavisni od pritiska, zapremine i temperature.

VARIJACIJA GASNE ZAPREMINE SA PRITISKOM BOJL-MARIOTOV ZAKON

VARIJACIJE GASNE ZAPREMINE ILI PRITISKA SA TEMPERATUROM

-Šarlov ili Gej Lisakov zakon-

Varijacija gasne zapremine sa temperaturom pri stalnom pritisku

Varijacija gasnog pritiska sa temperaturom pri stalnoj zapremini

JEDNAČINA GASNOG STANJA ILI KLAJPERONOVA JEDNAČINA

VANDERVALSOVA JEDNAČINA

DALTONOV ZAKON PARCIJALNIH PRITISAKA

AVOGADROV ZAKON

KINETIČKA TEORIJA GASOVA