Šarl-Ogisten de Kulon (Charles-Augustin de Coulomb, Angulem, 14. jul 1736. – Pariz, 23. avgust 1806.) francuski fizičar rođen u Angulemu. Bio je vojni inzinjer, i taj je posao obavljao tri godine, do povrede koja mu je veoma ugrozila zdravlje, na Martiniku. Na povratku zaposlio se u La Rochelleu. Godine 1781. Kulon je trajno stacioniran u Parizu. Pre početka revolucije 1789. Kulon daje otkaz na mestu `intendant des eaux et fontaines`, i odlazi penziju i prelazi na svoje imanje u Bloisu. Zatim biva ponovo pozvan u Pariz na konferenciju da bi se odredile nove merne jedinice, a sve to po naredbi Revolucionarne vlade.
Bio je jedan od prvih članova državnog instituta, a 1802. Postavljen je za inspektora javnih instrukcija. Nažalost, njegovo zdravlje je već tada bilo načeto, te je umro četiri godine kasnije u Parizu.
Najpoznatiji je po otkrivanju zakonitosti u elektrotehnici, koja je nazvana Kulonov zakon, a kojom je definisana elektostatička sila privlačenja i odbijanja.
SI jedinica za naelektrisanje u Međunarodnom sistemu nosi ime po njemu – Kulon (C).

Slika 1. Šarl-Ogisten de Kulon

Jednostavnim eksperimentom može se pokazati da kao rezultat međusobnog trljanja (trenja) neki materijali pokazuju svojstvo koje se naziva elektricitet (od grčke reči elektron). Ako na primer trljamo štapić od jantara (plemenita smola) vunenom krpom, natrljani štapić pokazuje svojstvo privlačenja sitnih predmeta, kao što su komadići papira. Sličan fenomen iskazivanja privlačne sile pokazuje i stakleni štap natrljan svilenom krpom. Kao rezultat trenja javlja se električna interakcija tj. električna sila koja može nadvladati silu gravitacije. Za razliku od sile gravitacije koja je uvijek privlačna, rezultat električne interakcije naelektriziranih tela može biti privlačna ili odbojna sila. Na primer, dva prethodno natrljana staklena štapa međusobno se odbijaju. Temeljem spomenutih eksperimenata može se zaključiti kako postoje dvije vrste naelektrisanja. Američki fizičar B. Frenklin smatrao je elektricitet jedinstvenim fluidom koji je imanentan svakoj materiji i koji onda može prelaziti s jednog tela na drugo.Sa obzirom na tadašnja znanja zaključak je bio logičan, ali kako se kasnije pokazalo, neispravan. Ne radi se o fluidu, nego je stvarni uzrok stvaranja statičkog elektriciteta trenjem u unutrašnjoj strukturi materije. Frenklina ovde spominjemo, jer je uveo pojmove pozitivnog i negativnog elektriciteta. Pri tom je smatrao da je telo pozitivno elektrisano, ako mu je količina elektriciteta veća od normalne, odnosno negativno za količinu elektriciteta manju od normalne.
Eksperimenti pokazuju da sile izmedju električnih opterećenja nisu iste kada opterećenja miruju i kada se kreću u odnosu na posmatrača. Najprostiji slučaj je kada sva opterećenja makroskopski miruju. (Naravno, na mikroskopskoj skali takvo stanje ne postoji.).
Deo fizike i elektrotehnike koji proučava sisteme vremenski nepromenljivih opterećenja na nepokretnim telima naziva se elektrostatika.
Elektrostatika je posebno područje elektrotehnike koje proučava međudelovanje električnih naboja u stanju mirovanja. U okviru elektrostatike postoje prostiji i složeniji slučajevi. Najprostiji za razmatranje su slučajevi naelektrisanih provodnih tela koja se nalaze u vakuumu (dakle, kada dielektrici nisu prisutni).
Elektrostatika se temelji na eksperimentalno utvrđenom inverznom kvadratnom zakonu. Do tog je zakona došao 1785. god., nakon niza eksperimenata, francuski fizičar Kulon.

KULONOV ZAKON

Nalektrisano telo je je telo na kome postoji višak bilo pozitivnih bilo negativnih opterećenja. Dva naelektrisana tela se privlače ako su im naelektrisanja suprotnog znaka,a odbijaju ako su im opterećenja istog znaka. Kulonov zakon proučava kako ta sila privlačenja zavisi od količine naelektrisanja na telima i njihovog rastojanja.
Kulonov zakon opisuje silu izmedju dva naelektrisana tela dije su dimenzije znatno manje od njihovog rastojanja. Takva dva naelektrisana tela se nazivaju punktualna ili tačkasta opterećenja. Treba uočiti da, po definiciji, punktualno opterećenje ne mora biti malih dimenzija niti nekog posebnog oblika, već samo da mora biti malo u odnosu na odstojanje do drugog opterećenja. Na primer, i dva naelektrisana tela oblika i veličine knjige nazivaćemo ,,punktualna opterećenja", pod uslovom da su daleko jedno od drugog.
Kulonov zakon predstavlja osnovni zakon elektrostatike i iz njega proističe praktično celokupna teorija elektrostatičkog polja.Kulon je do njega došao 1775 godine,nakon niza eksperimenata.
U radu je koristio posebni uređaj, tzv. torzionu vagu (slika 2.). Kasnije je upotrebom sličnog uređaja Kevendiš odredio gravitacionu konstantu g. Kulon je vršio eksperiment sa naelektrisanim telima menjajući količinu naelektrisanja Q1 i Q2 na njima i postavljajući ih na različite međusobne udaljenosti r.

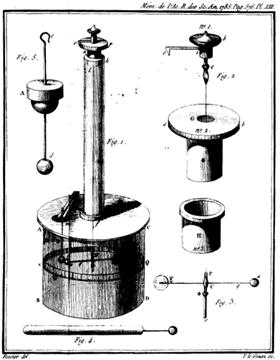
Slika 2. Kulonova torziona vaga

Došao je do konačnog oblika Kulonovog zakona za elektrostatiku čija je definicija:

Dva naelektrisana tela (čestice) se međusobno privlače ili odbijaju silom koja je upravno srazmerna proizvodu njihovog naelektrisanja, a obrnuto srazmerna kvadratu rastojanja izmedju ta dva tela.

Matematički izražen zakon glasi:

(1)
Pri čemu je:
F - Električna sila,
K - Kulonova konstanta (zavisi od sredine u kojoj se tela nalaze),ako se tela nalaze u vakuumu, ova konstanta iznosi
Q1 i Q2 - Naelektrisanja tih tela,
r - Rastojanje između tih tela
Merenja koja su opisana izvšena su u vazduhu. Pokazuje se, medjutim, da se isti rezultati za silu dobijaju i ako se eksperimenti vrše u vakuumu, pa je vrednost konstante k je praktidno ista i za vakuum. Uobičajeno je da se ta konstanta piše u obliku:

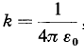
Prema tome i Kulonov zakon može da se napiše na sledeći način:

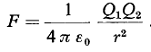(2)

Ovo je algebarski oblik Kulonovog zakona. Da bi bio potpun, ovaj oblik zahteva još i sledeće tumačenje rečima: Sila izmedju opterećenja je odbojna ako su opterećenja istog znaka, a privlačna ako su suprotnog znaka.(Slika 3. i 4.)

Dati matematički oblik Kulonovog zakona ne daje potpunu predstavu o delovanju Kulonove sile. Potrebno je još tumačiti odnos polariteta naelektrisanja za određivanje odbojnosti, odnosno privlačnosti sile.
Sila kojom naelektrisanje djeluje na naelektrisanje može se predstaviti kao:

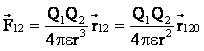
a sila kojom naelektrisanje djeluje na naelektrisanje:

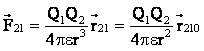
gde su:

- vektor položaja naelektrisanja u odnosu na centar delovanja naelektrisanja ,
- vektor položaja naelektrisanja u odnosu na centar delovanja naelektrisanja ,
i - jedinični vektori vektora i .

Smer sila zavisi od vrsta naelektrisanja. Ukoliko su oba istog polariteta sila je odbojna, a ukoliko su različitog polariteta onda je sila privlačna.

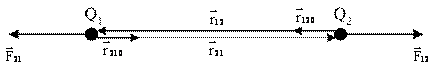
Slika 3. Predstavljanje vektora sile za dva naelektrisanja istih polariteta (odbojna sila).

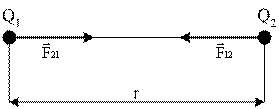
Slika 4. Predstavljanje vektora sile za dva naelektrisanja različitih polariteta (privlačna sila).

Primeri

Primer 1. Dve jednake kuglice poluprečnika a=2mm naelektrisane su istim količinama
elektriciteta Q. Pomoću torzione vage izmerena je odbojna sila izmedju njih od
kada su kuglice bile na rastojanju r = 2 cm. Odredimo naelektrisanje Q.

Dimenzije kuglice su male u odnosu na njihovo rastojanje, pa je sila izmedju njih data Kulonovim zakonom (2).
Ako u Kulonovom zakonu (2) stavimo Q1 = Q2 = Q i rešimo jednačinu po Q, dobijamo:

Da bismo izračunali Q, moramo sve veličine koje su date da izrazimo u jedinicama MKSA sistema. Tako dobijamo:

Dolazimo do zaključka da je ovo i suviše mala vrednost naelektrisanja.Medjutim,na ovako malim kuglicama u vazduhu je nemoguće ostvariti veće naelektrisanje od ovoga.

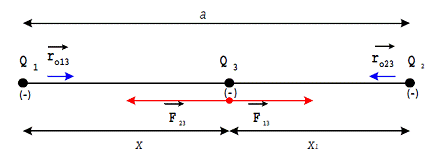
Primer 2. Dva tela, naelektrisana količinama naelektrisanja Q1=-4nC i Q2=-1nC, nalaze se na rastojanju a=18cm u vakuumu.
Kakav znak može da ima naelektrisanje trećeg tela, koje je naelektrisano količinom naelektrisanja Q3 = 1nC, i gde ga je potrebno postaviti da bi bilo u ravnoteži u odnosu na dejstvo Kulonovih sila prva dva tela?

Zadatak se rešava primenom Kulonovog zakona (2) i principa superpozicije.
F12 je električna sila kojom telo 1 deluje na telo 2. Vektor F12 mora ležati na pravoj koja spaja dva tela, a njegov početak, tj. tačka gde deluje, je u nekoj tački tela 2. Sa r012 obeležen je jedinični vektor usmeren od tela 1 ka telu 2. Ako su Q1 i Q2 istoga znaka njihov proizvod je pozitivan, i smer vektora F12 je u smeru vektora r012, odnosno sila je odbojna. Ako su naelektrisanja Q1 i Q2 suprotnog znaka, njihov proizvod je negativan, pa je smer vektora F12 u smeru vektora –r012, tj. sila je privlačna.

Prema principu superpozicije ukupna električna sila kojom na neko malo naelektrisano telo deluje više drugih malih naelektrisanih tela jednaka je vektorskom zbiru sila kojima ta druga tela deluju ponaosob na posmatrano telo.
(1) Q 3 > 0
Pretpostavimo da je naelektrisanje Q3 pozitivno naelektrisano. Ako je Q3 pozitivno, sile su privlačne. Ukupna sila koja deluje na ovo telo mora biti jednaka nuli kako bi bio ispunjen uslov da je telo u ravnoteži, i iz tog uslova može se odrediti gde je potrebno postaviti telo.

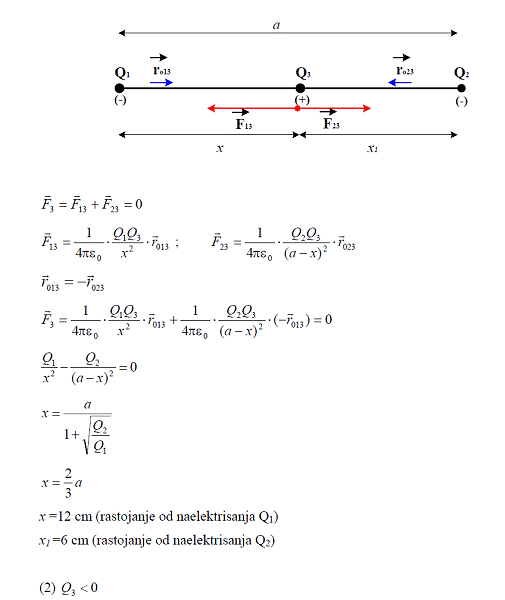
Ako je naelektrisanje Q3 negativno, sile su odbojne. Ukupna sila koja deluje na naelektrisanje Q3 mora biti nula da bi telo bilo u ravnoteži u odnosu na dejstvo Kulonovih sila prva dva tela.

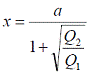
Literatura i linkovi

- Dr.Branko D Popović – Osnovi Elektrotehnike I, Gradjevinska knjiga Beograd 1976.
- Ljubo Malešević – Osnove Elektrotehnike II Dio – Elektrostatika,Studij Računarstva Split 2004.
- Sanja Maravić,Mikloš Pot – Zbirka rešenih ispitnih zadataka iz Osnova Elektrotehnike,Subotica 2002.
- http://hr.wikipedia.org/wiki/Coulombov_zakon
- http://en.wikipedia.org/wiki/Charles-Augustin_de_Coulomb

PROČITAJ / PREUZMI I DRUGE SEMINARSKE RADOVE IZ OBLASTI:

preuzmi seminarski rad u wordu » » »

Besplatni Seminarski Radovi