SEMINARSKI RAD IZ MULTIMEDIJA
OSTALI SEMINARSKI RADOVI
IZ MULTIMEDIJE |
|||||||||||||||
|
|||||||||||||||
DIGITALNO POLUTONIRANJE
Kućni štampači i računari su imali dramatičan udar na generisanje i
širenje značaja informacija u svijetu. U nekoliko decenija smo prešli
iz sistema u kojem je mogućnost da proizvedu i publikuju visoko kvalitetan
štampani materijal bila ograničena na relativno mali broj ljudi odnosno
firmi, u sistem u kojem su ove mogućnosti široko dostupne svima. Razvoj
algoritama digitalnog polutoniranja je bio ključ koji je omogućio ovu
transformaciju, posebno mogućnost štampanja slika. Digitalno polutoniranje
upućuje na proces dobijanja slike sa kontinalnim nijansama koristeći komponente
koje direktno mogu predstaviti relativno mali broj različitih nijansi.
Za predstavljanje svakog nivoa sivila algoritam polutoniranja generiše
kalup, takav da gledajući od strane posmatrača izgleda kao konstantan
nivo sivila.
Cilj algoritama polutoniranja je da generiše sliku koja se može štampati
standardnom namjenskom tehnologijom i tako posmstraču izgleda koliko je
to moguće kao slika sa kontinualnim tonovima. Takođe je bitno da broj
računskih operacija bude kompatibilan sa raspoloživim hardverom. Algoritmi
polutoniranja su počeli da se pojavljuju prije 30-ak godina i razvijani
su za komponente sa kompjuterski kontrolisanim grafičkim izlazom kao što
su ploteri.
U poslednjih 10 godina strahovit razvoj ink-jet štampača je podstakao
dalja istraživanja u oblasti polutoniranja. sada smo svjedoci rapidnog
porasta primjene digitalne fotografije. U 2004. godini prodaja digitalnih
fotoaparata je porasla za više od 25% u odnosu na prethodnu a u 2006.
godini se uduplala. Ovo će ubuduće ubrzati zahtjev za mogućnošću štampanja
visoko kvalitetnih fotografija sa ovih aparata. Kućni ink-jet štampači
koji koštaju oko 50 EUR mogu da reprodukuju slike sa skoro fotografskim
kvalitetom. Algoritmi za digitalno polutoniranje korišteni za izrađivanje
ovih slika su kritični za ostvarivanje tog nivoa kvaliteta. Kao i mnoge
aplikacije za obradu signala, velika moć poboljšanih algoritama je da
poveća kvalitet ili performanse sa malo ili nimalo povećanja cijene hardvera.
ovo je veoma atraktivno u trgovinama na veliko gdje gdje smanjenje cijene
od 1USD po komponenti može da uštedi mnogo miliona dolara. Digitalno polutoniranje
je velika oblast za istraživanje sa jakim vezama sa fizičkim svijetom
tako da je atraktivna za istraživače iz različitih oblasti kao što su
obrada signala, mašinstvo ili psihofizika. Prethodnih godina učinjen je
značajan razvoj algoritama i upotrebljenih modela i u komponentama za
izvršavanje algoritama i za ljudsku percepciju. Razvoj računarskih i tehnologija
izrade štampača kao i ekonomije, upravljao je tekućim istraživanjima.Trenutno
na tržištu vlada ogroman pritisak za smanjenje cijena. U isto vrijeme
rezolucija i brzina štampanja nastavljaju da konstantno rastu, Tako da
moramo odštampati više bita nego ikad i to po manjoj cijeni.
Jedna mogućnost je da prebacimo polutoniranje sa štampača na računar.
U ovom slučaju postaje neophodno kompresovati ovakvu sliku da bi vrijeme
prenosa između računara i štampača održali u razumnim granicama. Dok je
rasute tačke polutonirane slike, kao što se koristi kod ink-jet štampača,
ekstremno teško kompresovati, imamo novi izazov koji treba razmotriti.
Naime računska složenost dekompresije mora biti minimalna da ne poskupi
štampače. Inače ovim ne bi dobili ništa u odnosu na polutoniranje u samom
štampaču. Cilj ovog rada je da prezentuje napredak u poslednjih 10 godina
i da ukaže na oblasti koje je potrebno hitno istražiti u digitalnom polutoniranju.
S obzirom da je potreba za polutoniranjem usko povezana sa ograničenjima
izvršnih komponenti i s obzirom da je uspjeh polutoniranja jako zavisan
od ograničenja ljudskog vizuelnog sistema (HVS) čini se odgovarajućim
početi dijelom koji ispituje kako se na algoritme polutoniranja može uticati
poboljšanjem HVS i modela izvršnih komponenti. Ovaj dio daje uvod u 3
osnovne kategorije algoritama polutoniranja u cilju smanjenja složenosti
i računa, a to su: skrining, difuzija grešaka i iterativni istraživački
bazirani modeli. Razumjevajući kontekst u kojem algoritam polutoniranja
mora raditi, spremni smo i da razmotrimo u detalje specifične karakteristike
strukture polutoniranja koje imaju dobre vizuelne karakteristike i otporne
na poremećaje izazvane u samom štampaču. Naglasak na difuziju grešaka
je prikladan iz 2 razloga:
1. difuzija grešaka je pristup polutoniranju koji se najčešće koristi
u sadašnjim proizvodima, pored skrining metoda koje generišu periodično
grupisane uzorke tačaka koji oponašaju tradicionalne procese analognog
štampanja koji se koriste kod komercijalnih procesa za štampanje,
2. difuzija grešaka je u bliskoj vezi sa sigma-delta modulacionim postupkom
kodovanja signala koji je blizak onima u signal procesing sosajti.
Prva tema koja se razmatra je inverzno polutoniranje. To je značajno za
bilo koju aplikaciju u kojoj želimo izvršiti obradu slike koja je već
polutonirana. Takva situacija se pojavljuje kad se skenira odštampana
slika. Među interesantnim operacijama je i ona koja bi izvršila ponovno
polutoniranje tako da se može ponovo štampati. Sledeća tema je kompresija.
Pored potrebe da se kompresuje polutonirana slika unutar printera ili
između računara i štampača, kompresija polutoniranih slika takođe je potrebna
za efikasan prenos i čuvanje polutoniranih slika u širem kontekstu multimedijalnih
sistema.
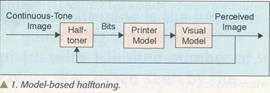
Digitalno polutoniranje zasnovano na modelima
Digitalno polutoniranje je proces generisanja uzorka piksela sa ograničenim
brojem boja koji, gledajući ljudskim okom, se vidi kao slika sa kontinualnim
tonovima. Ono se koristi za prikazivanje slika sa kontinualnim tonovima
u medijima u kojim je direktno prikazivanje nijansi nemoguće. Uobičajeni
primjer takvog medija je tinta ili toner na papiru, a uobičajena komponenta
za izvođenje takvih medija je štampač. Polutoniranje uspjeva zato što
oko radi kao prostorni NF filtar koji zamagljuje dobijeni uzorak piksela
tako da se on vidi kao slika sa kontinualnim nijansama. Iako se sve metode
polutoniranja oslanjaju, barem implicitno, na neko razumjevanje karakteristika
HVS i komponenti za prikazivanje, cilj tehnika polutoniranja zasnovanih
na modelu je razvoj eksplicitnih modela komponenti za prikazivanje i HVS
koji će maksimizirati kvalitet prikazanih slika. To je prikazano na slici
1. Zavisno od uključenog tipa izračunavanja, algoritmi za polutoniranje
se mogu svrstati u 3 kategorije:
1. lokalni algoritmi (skrining ili ditering)
2. globalni (difuzija grešaka)
3. iterativni algoritmi (najmanji kvadrati, direktna binarna pretraga
DBS).
Svi ovi algoritmi mogu ujediniti HVS i printer modele. Najbolje polutonirane
reprodukcije se postižu iterativnim tehnikama koje minimiziraju kvadratnu
grešku između izlaza iz printera u odzivu vizuelnog sistema na polutoniranu
sliku i odziva vizuelnog sistema na originalnu sliku.
UOPŠTENO O POLUTONIRANJU :
Razmotrićemo HVS modele. Iako se svi algoritmi polutoniranja zasnivaju
na činjenici da se oko ponaša kao NF filtar mnogi ne koriste eksplicitni
HVS model, i kao takvi se nesmatraju da su bazirani na vizuelnom modelu.
S druge strane, algoritmi polutoniranja bazirani na vizuelnom modelu eksplicitno
uključuju HVS model i koriste ga za kreiranje polutoniranih slika višeg
vizuelnog kvaliteta. Takođe se razmatraju displej modeli. Fokusiramo se
na crno-bijelim štampačima, ali mnoge ideje se praširuju na štampače u
boji. Za druge uređaje za prikaz kao što su displeji prenosnih uređaja
i posebno mobilnih telefona, mogu se koristiti tehnike slične onima koje
se koriste za štampače. Osnovne tehnike polutoniranja za crno-bijele štampače
pretpostavljaju da je primljeni nivo sive boje (štampanog binarnog uzorka)
proporcionalan rasporedu crnih tačaka u uzorku. Ustvari ovo znači da je
oblast koju zauzima crna tačkica približno jednaka oblasti koju zauzima
bijeli prostor koji octane tamo gdje nema ni jedne tačkice. Iz ovog slijedi
da je željeni oblik crnih tačaka koje printer proizvodi kvadrat TxT, gdje
je T veličina tačke. Ali stvarni štampači ne ispunjavaju ovu pretpostavku.
Iz čisto fizičkih razloga, štampači proizvode manje ili više kružne tačke
koje se prelivaju u susjedne prostore, čime se postiže da je primljeni
sivi nivo tamniji od onog pretpostavljenog. Ovo je preklapanje tačaka.
Vidjećemo kasnije da je neko minimalno preklapanje potrebno zato da bi
štampač mogao potpuno potamniti dio stranice. Uz to, mnogi štampači tipično
proizvode tačke koje izgledaju veće od ovih, a to je fenomen koji se naziva
dobitak tačke. Ovo može biti izazvano sa jednim ili više sledećih efekata:
optičko uvećanje (zbog raspršivanja svjetlosti ispod tonera)
mehanički dobitak (proširenje tonera na papiru)
dobitak električnog polja (koji se pojavljuje kod elektrofotografskih
printera).
Ako tehnika polutoniranja ne uzima u obzir takve nelinearnosti, rezultirajuća
skala tonova će biti iskrivljena. Klasični pristup ublažavanja gore navedenih
fenomena je grupisanje crnih tačaka tako da procentualno dejstvo na nivo
sivila bude smanjen. Ovakvo grupisanje smanjuje prostornu rezoluciju rezultujuće
slike i povećava vidljivost strukture polutoniranja. S druge strane algoritmi
polutoniranja sa cijepanjem tačaka mogu obezbjediti visoku prostornu rezoluciju
i odlične šeme polutonova, ali su vrlo osjetljivi na dobitak tačaka kao
i na druga izobličenja koja unosi štampač. Tehnike zasnovane na modelima,
s druge strane, se mogu pouzdati na ispravne printer modele (skoro u potpunosti)
izobličenja štampača da maksimiziraju kvalitet štampane slike. Prema tome
oni omogućavaju veću dobit od tehnika sa rascijepanim tačkama, za bilo
koji uređaj i bilo koji dostupan ispravan model.
Treći pristup je postupak korekcije tonova, a to je kmpenzujuća gray-scale
transformacija primjenjena na slici prije polutoniranja. Međutim ovaj
pristup ne daje dobru vidljivost detalja i ne može prilagoditi nivoe tonova
tako dobro kao tehnike zasnovane na modelima. Šta više za neke tehnike
(npr. kad štampač unosi nemonotone nelinearnosti) ova pristup uopšte neradi.
U dodatku, jer interakcija tačaka može biti veoma kompleksna, pristup
korekciji tonova ne radi dobro za tehnike sa rascijepljenim tačkama jer
je veoma malo kontrole nad mikro strukturom tačaka koje prozilaze iz istih.
Prema tome korekcija tonova je manje pogodna za štampanje sa rascjepljenim
tačkama sa elektrofotografskim štampačima. Predstavićemo izvjesnu klasu
printer modela da olakšamo implementacijutehnika baziranih na modelima
i ispitaćemo izvjestan broj specifičnih modela. Zatim će mo ispitati nekoliko
tehnika baziranih na modelu koje uključuju HVS i/ili printer modele da
unapredimo kvalitet polutoniranih slika tako da uključuju screening, difiziju
grešaka i iterativne algoritme (least squares i DBS). Za date komponente
za prikaz i uslove pod kojim se posmatra slika, performanse tehnika polutoniranja
npr. vizuelni kvalitet polutonirane slike koju prikazujemo, može se procjeniti
o izrazu za njegovu prostornu rezoluciju (sposobnost da prikaže detalje,
ivice i oštrinu), rezoluciju skale tonova (sposobnost da prikaže mnogo
različitih nivoa sivila), tačnost skale tonova (ugao pod kojim su prikazani
polutonovi vidljivi sa odgovarajućim nivoom sivila) i strukturu (koliko
je vidljiva ili neprijatna struktura koju uključuju polutonovi). Ove karakteristike
mogu biti posmatrane u različitim regionima slike. Prostorna rezolucija
utiče na regione veoma brze promjene intenziteta, kao što su ivice. U
regionima konstantnog intenziteta rezolucija i tačnost skale tonova su
bitni ako je potrebna egzaktna reprodukcija. Međutim, najbitnije razmatranje
je vidljivost struktura koje uključuju polutonovi. Najzad regioni sporo
promjenljivog intenziteta vjerovatno predstavljaju najveći izazov za tehnike
polutoniranja. Ovdje je najvažnija kompatibilnost susjednih nivoa tonova.
Ako susjedni nivoi tonova nisu izvedeni kompatibilnim obrascima polutoniranja,
onda će konture greške biti vidljive u regionima gdje se intenzitet sporo
mjenja. Ovaj efekat se pojavljuje iz dva razloga: 1. nedostatak adekvatne
rezolucije skale tonova i 2. nekompatibilnosti struktura tonova koji odgovaraju
susjednim nivoima tonova.
U tradicionalnim tehnikama polutoniranja (filtar za cijepanje tačaka), glavni kompromis (kontrolisan periodom filtra) je između prostorne rezolucije i strukture (niske vidljivosti) sa jedne strane i rezolucije i tačnosti skale tonova sa druge strane. Za razliku od ovog, kod difuzije grešaka i iterativnih tehnika, prostorna rezolucija je generalno veoma visoka, i glavni kompromis je između strukture i rezolucije skale tonova. Postoje, međutim, još neki bitni kompromisi. Npr. tehnika filtra za cijepanje tačaka je obično otporna na dobitak tačaka i ostale deformitete koje unosi printer, dok difuzija grešaka i iterativni metodi zasnovani na modelima nude bolju prostornu rezoluciju i strukturu za specifični uređaj. Kompromis između otpornosti na uzobličenja printera i strukture i prostorne rezolucije je jedan od ključnih uspjeha green-noise tehnike polutoniranja.
HVS Modeli
Polutoniranje uopšte radi jer je oko prostorni NF filtar tako da zamagljuje
uzorke štampanih tačaka, pa zato vidi nivoe sivog. Premda je svako polutoniranje
zasnovano na razumjevanju (tj. modelu) ljudskog vizuelnog sistema, određeni
metodi polutoniranja zasnovani na vizuelnom modelu će biti opisani kasnije.
U ovoj sekciji će mo opisati neke HVS modele koje ovi metodi koriste.
Postoje dva blisko povezana koncepta:
metrika vizuelne tačnosti reprodukcije (VF) i
HVS modeli.
VF metrika je funkcija V(z, zkapa) takva da jasno pokazuje sistem do kojeg
se slika zkapa različito vidi od slike z. U kontekstu polutoniranja, HVS
model je sistem S koji generiše S(z), koji je slika kao z, osim onih osobina
koje su pojačane ili oslabljene proporcionalno njihovoj vidljivosti. Postoji
bliska veza između ovih modela. Npr. dati HVS model S se može upotrijebiti
kao VF metrika računajući energiju različitih slika S(z)-S(zkapa). Ovaj
pristup je iskorišten u mnogim metodama polutoniranja zasnovanim na vizuelnom
modelu. Najjednostavniji HVS model je jednostavno dvodimenzionalni linearni
prostorno invarijantni filtar. Npr. sledeće frekventna karakteristika
dobro predviđa subjektivni kvalitet kodovane slike (Mannos & Sakrison)
![]() (1)
(1)
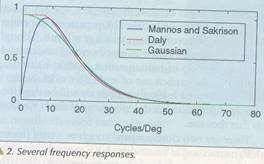
gdje je fr= (fx^2+fy^2)^1/2 RMS vrijednost horizontalne i vertikalne frekvencije u periodima po stepenu. Kao što je prikazano na slici 2 koja prikazuje H u funkciji fr, ovaj filtar je PO sa maksimumom u 7,9 perioda/deg. Mi posmatramo frekventnu karakteristiku kao predstavu osjetljivosti oka u funkciji frekvencije. Vršena je direktna estimacija osjetljivosti oka na svaku frekvenciju i onda iskorištena za definisanje frekvencijske karakteristike filtra u HVS modelu. takve osjetljivosti su tipično pronađene mjerenjem testa nejasnoće sinusoidalnog uzorka date frekvencije koja se mogla razlikovati od pozadine. Inverzna vrijednost amplitude sinusoide na pragu vidljivosti je mjera HVS osjetljivosti na odgovarajućoj frekvenciji, i crtana svaka osjetljivost u funkciji frekvencije je obično predložena kao funkcija osjetljivosti kontrasta. Smanjenje osjetljivosti na višim frekvencijama je posljedica optičkih karakteristika oka, tj. karakteristika sočiva i rožnjače. Zaista usvajanjem terminologije iz optike frekventna karakteristika modela se obično naziva modulaciona transfer funkcija (MTF) oka.
Smanjenje osjetljivosti oka na nižim frekvencijama je posljedica nemoći oka da prilagodi otvor zjenice uslovima osvjetljenja. Zbog ovoga oko teško razlikuje intenzitet velikih regiona sa konstantnim intenzitetom. Dobro je poznato da je oko manje osjetljivo na nakošene likove nego na likove orjentisane horizontalno ili vertikalno. Ovo može biti iskorišteno za korištenje filtra oblika
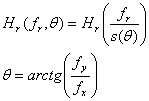 (2)
(2)
gdje je =arctg(fy/fx) odgovarajući ugao između fx i fy. Sledeći izbor za S()
![]() (3)
(3)
je iskorišten za metode polutoniranja zasnovane na modelu. Veliki broj
više sofisticiranih modela je bio predložen za HVS. Npr. neki modeli su
dodavali neke nelinearnosti prije linearnog filtriranja, a mnogi modeli
su uključivali banke filtara. Premda postoji još mnogo više soficistiranih
modela jednostavni modeli bazirani na filtrima su nadmoćni za korištenje
pri polutoniranju zasnovanom na vizuelnom modelu. Ovo je posebno izraženo
kod iterativnih metoda gdje se jednostavnost zahtjeva da bi metod uopšte
bio računljiv. Stoga, u ostatku ove sekcije ćemo se fokusirati na modele
koji su zasnovani samo na filtru. Za upotrebu u polutoniranju, HVS model
zasnovan na filtru (1) mora konvergirati u 3 aspekta:
- po frekvenciji u period/inch
- po prostornom impulsnom odzivu
- po odmjerenoj verziji imp odziva.
Konvergencija po frekvenciji je obezbjeđena sa
![]() (4)
(4)
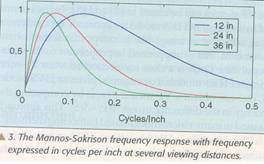
gdje je d udaljenost slike od oka. Kao ilustracija na slici 3 je predstavljen
impulsni odziv za 3 različite udaljenosti. Zbog toga što posmatrač ne
može biti na fiksnoj udaljenosti od slike, polutoniranje zasnovano na
vizuelnom modelu mora biti dizajnirano na neki domet HVS modela a ne samo
na jednu udaljenost. Ovo je razlog zbog kojeg se koriste NF filtri prikazani
na slici 2. Metode polutoniranja zasnovane na vizuelnom modelu koji uključuje
NF filtar će postati dobro vidljiv sa većih distanci gledanja. Prema tome
propisano je nekoliko NF filtara. Npr jedan uzima funkciju Hr a onda jednostavno
proširi vrh do 0, slika2. Druga mogućnost je Gausova frekventna karakteristika
sa standardnom devijacijom sigma=16,7 perioda po stepenu dobro aproksimira
ovaj filtar na višim frekvencijama. Konvertovanje frekventne karakteristike
u impulsni odziv se vrši pomoću inverzne Furijeove transformacije. Tipično,
filtar je u metod polutoniranja implementiran u prostornom domenu pomoću
direktne konvolucije. Dok su slike i polutonovi, naravno, odmjereni impulsni
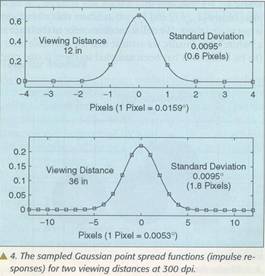
odziv filtra mora biti ograničen i odmjeren. Npr. slika 4 prikazuje Gausov
filter sa slike 2 ograničen na interval +-0,064 stepena odmjeren pod 2
različite okolnosti. Generalno ako b() označava (jednodimenzionalan)
impulsni odziv gdje je u stepenima tada je ograničen i odmjeren impulsni
odziv
![]() (5)
(5)
gdje je d udaljenost gledanja, R rezolucija piksela u dpi slike i polutona, min i max specifiraju stepene do kojih je impulsni odziv ograničen. Treba napomenuti da u slučaju niske rezolucije i bliske distance gledanja dizajniranje filtra treba uraditi mnogo pažljivije da se izbjegne preklapanje spektra. Prethodna relacija zavisi od R i d samo kao njihov porizvod tako da S=d*R postaje kjučni parametar i naziva se faktor skale. On se može interpretirati kao viđena rezolucija u dots/rad, gledane slike štampane sa R dpi sa udaljenosti d. On takođe ima bitan uticaj na uzorke polutoniranja nastale kao algoritmi zasnovani na HVS. Velika vrijednost d govori algoritmu polutoniranja da će oko mnogo zamagliti sliku i njenu polutoniranu reprezentaciju. S druge strane mala vrijednost d govori algoritmu da su tačke i ostali finiji detalji više vidljivi. U ovom slučaju algoritam će mikro upravljanjem postavke tačaka stvoriti finiju strukturu. Promjena R ima sličan efekat. Takođe je interesantno razmisliti o efektu promjene s na odmjereni impulsni odziv. Kad je faktor skale s malen, odmjereni impulsni odziv ima mali broj članova, tj. nekoliko nenultih članova jer su odmjerci b() široko razdvojeni. Stoga kad algoritam polutoniranja traži uzorak za poluton za dio sa konstantnim nivoom sivila, on radi sa malim brojem tačaka. Ovo znači da može generisati samo mali broj nivoa sivila što uzrokuje da skala tonova bude gruba. Šta više, za neke nivoe sivila, ovo će težiti da bude jedinstven obrazac koji će imati željeni nivo sivila i najbolju strukturu. Ovo u kombinaciji sa niskom rezolucijom gray-scale nivoa teži da uzrokuje nepostojeće konture. Objasnimo ovo na regionu sa postepenim povećanjem nivoa sivila. Tada će postojati imaginarna linija sa one strane sa koje je algoritam dosljedno postavljao jedan uzorak tačaka dok je sa druge strane postavljao drugačiji uzorak. Rezultat je lažna vidljiva konturna linija.
S druge strane kad je faktor skale velik odziv filtra će imati mnogo odmjeraka dajući algoritmu veću fleksibilnost u odabiranju najboljih uzoraka da napravi mnogo nivoa sivila bez lažnih kontura. Rezultujući polutonovi će težiti da budu grublji ali ne vidljivi sa veće distance gledanja. Zbog toga što faktor skale ima takav uticaj na prirodu polutoniranih reprodukcija onda o njemu treba voditi računa čak i kad je distanca gledanja unaprijed poznata. U ovom slučaju treba izabrati s kao kompromis između finijih struktura polutonova sa jedne strane i finije rezolucije skale tonova i izbjegavanja lažnih kontura sa druge strane. Pokazano je da ne postoji jedan set vrijednosti parametara koji daju najbolje rezultate na cijeloj skali tonova. Koristi se pristup dualne metrike koji koristi veći faktor skale na svjetlijim površinama, srednjim tonovima i sjenkama, a manji faktor skale u ostalim djelovima.
Printer modeli
Svrha printer modela je da tačno pretpostave stvarni nivo sivila koji printer štampa. Pored toga on treba jednostavno da uključi i algoritam polutoniranja. Sa preciznim printer modelom tehnika polutoniranja može da poveća karakteristike printera tj. da poveća kvalitet štampanih slika. U prvoj aproksimaciji elekrofotografski printeri su sposobni da naprave crne mrlje (obično zvane tačke) na komadu papira obično kvadratnog oblika piksela sa horizontalnom i vertikalnom dužinom Tx i Ty u inčima. Recipročne vrijednosti Tx i Ty vertikalna i horizontalna rezolucija štampača u dpi. Koristićemo sledeću terminologiju. Piksel (i,j) je kvadrat Tx*Ty čiji je centar tačka (xi,yj), xi=i*Tx+Tx/2 je udaljenost od lijeve strane slike i yj=j*Ty+Ty/2 je udaljenost od vrha slike. Kolekciju svih piksela tj. svih tih pravougaonika nazivamo štampana rešetka.
Printer kontroliše Nx*Ny binarno polje bi,j gdje bij=1 označava crnu tačku
koju treba staviti u centar piksela (xi,yj), a bij=0 označava da crna
tačka tu ne treba. Ponekad ćemo reći da je to bijela tačka. Konačno pretpostavimo
da je gray-scale slika (koju treba polutonirati) odmjerena tako da treba
štampati jednu tačku po pikselu. Ako to nije slučaj neophodna je interpolacija.
Prema tome takođe je definisano Nx*Ny polje zij koje uzima vrijednosti
iz intervala 0 1 . Pretpostavimo da te vrijednosti (nivoi sivila) predstavljaju
apsorpciju svjetlosti. Napokon nivo sivila crne tačke će biti 1, a nivo
sivila bijele tačke će biti 0. Reflektansa će biti 1-apsorptansa. Još
pretpostavimo pretpostavimo da je broj piksela slike jednak broju polja
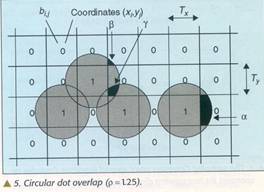
štampane rešetke. U prvoj aproksimaciji printeri štampaju skoro kružne
tačke kao na slici 5. U zavisnosti od tehnologija štampača, veličina,
oblik, gustina boje (a odavde i uniformnost apsorpcije) i mjesto postavljanja
crnih tačaka može da se mjenja. Napokon današnji elektrofotografski (laser
i LED) štampači uključuju modulaciju tačaka (npr. mjenjanje mjesta štampane
tačke) pa stoga svaki piksel može da bude u jednom od nekoliko stotina
stanja. U svakom slučaju oblast koju kontroliše štampač će imati više
od 2 vrijednosti. U sledećem razmatranju ćemo pretpostaviti binarni štampač
ali se ideje mogu proširiti i na opšti slučaj.
Odmjereni gray-scale printer model (SGPM)
Ovdje ćemo opisati klasu printer modela koji čine temelj tehnika polutoniranja
zasnovanih na modelu. Glavna ideja je procjeniti prosječan nivo sivila
svakog piksela štampane slike kao funkciju vrijednosti binarnog polja
u okolini tog piksela. Odavde se nagovještava da je ovo veoma komplikovana
funkcija.
Neka je u(s,t) nivo sivila štampane slike u tački (s,t) gdje je s udaljenost
od lijevog, a t udaljenost od gornjeg kraja slike. Tada je:
![]() (6)
(6)
gdje je Bs,t oznaka rasporeda bita u okolini ove tačke, a f neka funkcija. Kao što ćemo vidjeti ova funkcija može biti deterministička ili slučajna. Međutim, podesno je zbog malog razmaka između tačaka i ograničene prostorne rezolucije oka nivo sivila u(s,t) štampane slike modelirati konstantnom vrijednosti pi,j unutar oblasti piksela:
![]() (7)
(7)
gdje je (xi,yj) koordinata centra piksela. Premda nivo sivila nije baš konstantan, oko raspoznaje samo srednji nivo sivila u ovoj oblasti. To je taj srednji nivo sivila koji predstavlja pi,j tj., srednja vrijednost f(s,t,Bi,j) u ovoj oblasti. Prema tome srednja vrijednost sivila pi,j zavisi od susjednih piksela na sledeći način:
![]() (8)
(8)
gdje je wi,j prozor koji sačinjavaju biti bi,j u nekoj njegovoj okolini
i P označava neku njegovu funkciju. Primjetimo da je printer model jednoznačno
određen funkcijom P koja kao i funkcija f može biti deterministička ili
slučajna. Prema tome dato binarno polje bi,j secificira šablon tačaka
za štampu, printer model generiše novo polje pi,j nivoa sivila istih dimenzija
kao i binarno polje jednako dobro kao i gray-scale slika. Ovo je veoma
važno jer čitava obrada može biti urađena u diskretnom domenu bez ikakve
potrebe za naknadnim preodmjeravanjem. Ovaj model je nazvan SGPM.
Razmotrimo načine dobijanja funkcije P. Varijacije gore navedenih fenomena
utiču na izgled odštampane slike, a jedino mjesto gdje ih možemo uključiti
u model je funkcija P. Za efikasno izračunavanje neophodno je da w bude
malen prozor npr. 3x3. U ovom slučaju moguće vrijednosti funkcije P se
mogu upisati u tabelu sa 2 na 9 elemenata. Pojedinačni elementi ove tabele
mogu se izvesti iz detaljnog fizičkog razumjevanja varijacija fenomena
ili mjerenjem nivoa sivila koji se dobiju štampanjem svih uzoraka. Jedan
pristup koristi model preklapanja kružnih tačaka.
Model preklapanja kružnih tačaka (CDOM)
Jedan od najjednostavnijih printer modela pretpostavlja da printeri proizvode tačke kružnog oblika, kao na slici 5. Tačke su zasićene tako da u oblastima preklapanje nema dodatnog tamnjenja (logičko ili). Zbog jednostavnosti pretpostavićemo da su pikseli kvadrati (tj. Tx=Ty=T). Podsjetimo da se susjedne crne tačke mogu preklopiti i da mogu pokriti dijelove piksela sa bijelim tačkama. Poluprečnik tačaka mora biti najmanje T/sqrt(2) tako da mogu potpuno potamniti region ili cijelu stranicu. Ovo znači da uvijek postoji neko preklapanje između crnih tačaka i potamnjenje dijelova bijelih tačaka, što rezultuje povećanjem nivoa sivila piksela koji predstavlja bijela tačka. Ovo rezultuje značajnom distorzijom štampane slike (područje svake tačke je 1,57 T*T tj. 57% veće od T*T kvadrata) Većina printera proizvodi veće crne tačke od ovih minimalnih, što povećava distorziju nivoa sivila. CDOM računa svako izobličenje procjenom nivoa sivila svakog piksela štampane slike kao procenta površine piksela pokrivene tintom. Ova oblast može se lako izračunati iz radijusa tačke. Mnogo specifičnije, printer model uzima oblik
![]() (9)
(9)
gdje prozor wi,j uključuje bi,j i njegovih 8 susjednih piksela.
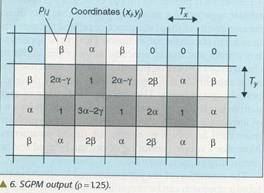
Ovdje f1 predstavlja broj horizontalnih i vertikalnih susjednih crnih tačaka, f2 je broj dijagonalnih susjednih crnih tačaka koje nisu susjedne nijednoj horizontalnoj ili vertikalnoj susjednoj crnoj tački, i f3 je broj parova susjednih crnih tačaka gdje je jedna vertikalna susjedna, a druga horizontalna susjedna tačka. Parametri alfa beta i gama su odnosi površine pokrivenih regiona prikazanih na slici 5 i Tkvadrat i mogu biti izraženi u zavisnosti od odnosa ro poluprečnika ove tačke i idealnog poluprečnika tačke T/sqrt(2). prema tome, parametar ro potpuno specificira printer model. Za klasične crno-bijele printere vrijednost ro je između 1 i 1,7. Slika 6 prikazuje izlaz SGPM za uzorak tačaka sa slike 5 i ro=1,25. Model nije mnogo osjetljiv na male promjene ro i primjenjuje se u širokoj klasi printera. podsjetimo da ovaj model uzima u obzir i mehanički i optički dobitak tačke.
Tabelarni modeli
Kao što smo vidjeli printer model procjenjuje nivo sivila (npr. apsorptanse)
svakog piksela štampanog uzorka kao funkciju vrijednosti binarnog polja
bi,j u okolini tog piksela (jednačina 8). Ovakva funkcija može biti određena
jednačinom, kao kod CDOM, ili tabelom vrijednosti nivoa sivila za svaki
ulazni uzorak.
Modeli kao što su CDOM su prilagođeni mnogim printerima ali nemogu da
opišu ponašanje svakog printera. Stoga različiti modeli mogu biti izvedeni
za različite tehnologije štampe ili različite rezolucije štampe. Za neke
printere, interakcija tačaka može biti veoma kompleksna i izvođenje modela
zasnovano na fizičkom razumjevanju procesa štampanja može biti preteško
ili prekomplikovano. Da bi se izbjegli mnogi problemi predložen je tabelaran
pristup modelovanju printera koji koriste direktno mjerenje apsorpcije
odštampanih test šara po redosljedu koji je u tabeli. To može biti primjenjeno
na bilo koji printer. Taj prilaz je baziran na makroskopskom mjerenju
apsorpcije specijalno dizajnranih test šara koje se periodično ponavljaju.
Prosjek apsorpcije svke šare je u vezi sa parametrima printera vezan sistemom
linearnih jednačina. Bitno je da se može upotrijebiti jednostavna komponenta
za mjerenje i ne zahtjeva se precizno centriranje. Procjena parametara
u tabelarnoj procjeni može biti pojednostavljena razmatranjima ako su
dostupne komponente visoke rezolucije za mjerenje apsorptanse svakog pojedinačnog
piksela. Ovo eliminiše potrebu za rješavanje sistema jednačina za dobijanje
vrijednosti parametara ali zahtjeva precizna podešavanja. Predložen je
mikroskopski pristup koji koristi skener visoke rezolucije (4000 dpi)
da izmjeri apsorptansu centralnog piksela za sve moguće 3x3 uzorke. Da
se riješi problem centriranja štampaju se karakteristične krive oko svakog
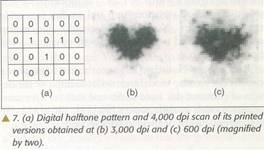
uzorka i procjenom njihovog centra određuje se centar uzorka. Slika 7
prikazuje skeniran visokom rezolucijom izlaz HP laser-jet 4M printera
za uzorak sa slike 7a. Primjetimo da je 600 dpi uzorak sa slike 7c povećan
2 puta tako da je iste veličine kao i 300 dpi uzorak sa slike 7b. Primjetimo
takođe da pri 300 dpi CDOM može jasno predvidjeti jasnu razumnu aproksimaciju
printera, ali bi bilo teško da predvidi isti model pri 600 dpi. Pronađeno
je da 600 dpi uzorci nisu toliko stabilni kao 300 dpi uzorci što je neophodno
pri upotrebi stohastičkih printer modela.
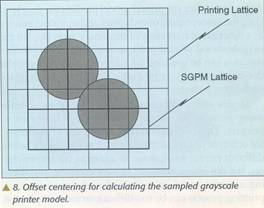
Model pomjeranja centra
Opisali smo SGPM koji procjenjuje nivo sivila svakog mjesta piksela u štampanoj rešetki tako da oni proizvode gray scale sliku koja predstavlja izlaz printera na istoj rešetki kao što je štampana rešetka. Međutim postoje i druge mogućnosti. Npr. kao na slici 8 umjesto procjene nivoa sivila na svakom mjestu štampanog piksela, SGPM može da procjeni nivo sivila na mjestima piksela centriranim u uglove štampanih piksela. Drugim rječima, rešetka na kojoj je SGPM bazirana može da ima određen pomjeraj u odnosu na štampanu rešetku. Prednost ovoga je što sada svaki piksel u printer modelu ima samo 4 susjedna piksela, a ne 8 kao kad nije bilo pomjeraja. Prema tome, sada je dovoljna 2x2 tabelarni model za efekte najbližih piksela koji ima svega 2^4=16 članova za razliku od 512 za 3x3 model. ovo je velika ušteda. Naravno, on nije potpuno tačan kao 3x3 model. Ipak sada umjesto 3x3, 5x5, 7x7, ... okolina imamo 2x2, 4x4, 6x6, ... okoline.
Model za ink-jet štampače
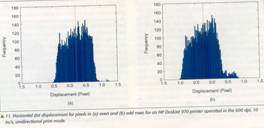
Ink-jet štampači štampaju tako što glava štampača sa mnogo malih mlaznica prelazi preko papira i izbacuje kapljice tinte iz mlaznica. Glava štampača može da sadrži mlaznice za jednu ili više boja, npr. cijan, magenta i žuta, i svakoj boji su tipično pridružene dve kolone mlaznica, tako da za trikolor glavu štampača imamo 6 kolona mlaznica. Ovi štampači proizvode stabilne tačke velikog integriteta, međutim oni pokazuju greške pomjeranja i neregularnosti tačaka zbog razdešenosti glave štampača, dinamičkog pokreta glave, oblika kapljice, turbulencije u vazduhu između glave i površine papira. Greške pomjeranja tačaka uzrokovane ovim fenomenima pokazuju slučajne osobine. Ovi štampači podržavaju veliki broj opcija štampanja, kao što su različita rezolucija, brzina, smjer, broj prolaza kroz štampu i broj kapljica tinte po svakom pikselu. Rezultujuće greške su veoma zavisne od načina štampanja. Generalno, sporije štampanje će rezultovati manje vidljivim greškama. Štampanje u više prolaza se obično koristi da redukuje broj grešaka štampanja. Kod štampanja u više prolaza, glava prelazi preko svakog piksela više od jedan put i ispušta kapljicu tinte prilikom pouzdanog prolaza. Za kontrolu ovog procesa se koristi binarno polje zvano maska štampanja. Za siguran mod štampanja, greška pomjeraja tačke može uzrokovati karakteristične produkte u štampanoj strukturi polutonova, kao što je prikazano na slici 10. Ovi produkti mogu biti stvarni tragovi tako što tačke štampane u parnim vrstama budu pomjerene desno sa obstupanjem od 0,25 piksela, a one štampane u neparnim vrstama budu pomjerene lijevo za 0,25 piksela. Slika 11. pokazuje pokazuje histograme horizontalnog pomjeraja tačaka za parne i neparne vrste. Ova odstupanja su posljedica konstrukcije glave štampača. Sa slike 11 se takođe vidi da su ova odstupanja slučajna sa uniformnom raspodjelom preko cijelog intervala do dimenzija piksela. Stohastička priroda ovog efekta dodaje naknadni nivo složenosti modela i usko povezuje ovaj stepen modeliranja sa metrikom grešaka iskorištenoj u samom algoritmu polutoniranja.

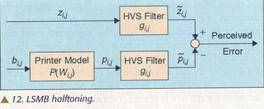
Algoritmi polutoniranja zasnovani na modelu
Metod najmanjih kvadrata zasnovan na modelu (LSMB) sa direktnom binarnom pretragom (DBS)
Sada ćemo, za date precizne modele za HVS i komponente za prikaz, razmotriti
algoritme kojima maksimiziraju kvalitet prikazanih slika korištenjem metrike
tačnosti. U LSMB pristupu ovo uzima formu minimiziranja kvadratne greške
između izlaza vizuelnog sistema pobuđenog štampanom polutoniranom slikom
i izlaza vizuelnog modela pobuđenog originalnom slikom sa kontinualnim
tonovima. Kao što ćemo vidjeti kasnije optimalna varijanta, u ovom smislu
optimalna polutona reprodukcija, može se jedino dobiti iterativnim tehnikama
koje pretragom cijelog prostora svih mogućih polutonih slika izabiraju
one koje minimiziraju kriterijum greške. Zbog toga što je tipična specifikacija
polutonova binarna za ovaj proces se predlaže DBS. Cjelokupan ovakav pristup
je poznat kao DBS ili LSMB pristup. Sada posmatramo detaljniju formulaciju
problema. Neka zij označava sliku kontinulanih tonova. Kao što je prikazano
na slici 12 LSMB pristup traži polutoniranu sliku bij koja minimizira
kvadratnu grešku:
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
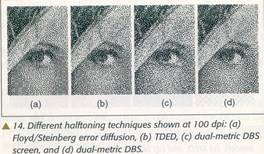
Ovdje se Wij sastoji od bij i njenih susjeda, a * ukazuje na konvoluciju. Granični uslov pretpostavljuju da boja nije postavljena iznad granica slike. U principu optimalno rješenje se može dobiti iscrpnom predragom svih mogućih binarnih šema za cijelu sliku. Ovaj pristup ipak nije računski izvodljiv. Broj mogućih šema za sliku je (na primjer 1.16*1077 samo za sliku 16x16). Tako, rješenje sa najmanjom kvadratnom greškom se mora dobiti tehnikama iterativne optimizacije. Takve tehnike nalaze rješenje koje je samo lokalni optimum. One pretpostavljaju da je data početna procjena slike. Na primjer to bi mogla biti neka trivijalna slika kao što je konstanta ili slučajna slika ili izlaz nekog algoritma polutoniranja. Zavisno od strategija optimizacija, vizuleni kvalitet rezultujuće polutonirane slike može da zavisi od početne slike. Strategija za pretraživanje za koju je pokazano da vrlo dobro radi presjeca sliku kao rastersko pretraživanje. Na svakom pikselu razmataramo prebacivanje stanja tog piksela sa jedan na nula i sa nula na jedan koje je odgovarajuće u tom trenutku, a takođe i zamjenu stanja toga piksela stanjem bilo kojim od njegovih najbližih osam susjeda, ako su različite. Među ovih devet mogućih promjena uzimamo onu jednu promjenu , ako postoji, koja smanjuju ukupnu grešku najviše (12). Kad HVS filtar ima konačan impulsni odziv, binarna vrijednost svakog piksela utiče samo na izlaze modela PKL u njegovom susjedstvu i takva greška se računa samo lokalno. Ovdje treba napomenuti da vrijednost greške ne trega računati od početka svaki put. Vrijednost Zij se nekada ne mjenja sam nekoliko izraza u konvolucionoj sumi koja određeju Pj se mora updateovati (oni koji uključuju tekući piksel i njegove susjede). Iskorištavanjem bilinearnosti metrike greške možemo postići veliku redukciju koštanje procjene promjena pod O(Ώ(gij)) aritmetičkih operacija gdje je Ώ(gij) broj piksela koji podržavaju filtar gij za mali broj aritmetičkih operacija nezavisnih od gij. Iteracija je kompletna kada se minimizacija izvede jednom za svaki piksel slike. Broj iteracija zavisi od početne slike i efektivne širine filtra. Slike 13 a i b pokazuju uvećan detalj gray – scale linearne promjene polutonirane sa LSMB korištenjem HVS filtera koji odgovaraju distancama gledanja od 0.5 i dvije stope ne 300 dpi. Zapazimo da kao što je ranije pretpostavljeno kako se razdaljina posmatranja povećava šeme postaju grublje. Ako se svaka slika posmatra sa prave razdaljine broj opaženih sivih nivoa bi trebao da se povećava sa grubljim šemama. To je posljedica koja je direktno povezana sa grubošću skale tonova. Specifično za tačke udaljenije nego što oko može da primjeti LSMB metrika nalazi da je bolje neproizvoditi tačke koje predstavljaju skoro bijela područja radi nego smještanje nekoliko široko razdvojenih tačaka. Slika 13c pokazuje lineranu zavisnot polutoniranom dualnom metrikom DBS koje smo diskutovali ranije. Ovaj pristup efektivno mijenja razdaljinu posmatranja u cilju poboljšanja polutonskih šema u različitim dijelovima slike. Slika 14 prikazuje uvećan detalj slike polutonirane različitim metodama.

Difuzija grešaka bazirana na modelu
Algoritma difuzije grešaka je globalna tehnika koja proizvodi oštrije slike nego point tehnike i genriše vizuelno prijatnije šeme za oko. Međutim ova tehnika je veoma osjetljiva na preklapanje tačaka i druga izobličenja štampača. Zato je neophodno uključiti model štampača u algoritmu.
Difuzija grešaka bazirana na modelu štampača
Glavna ideja za difuziju grešaka je veoma jednostavna. Kao što je prikazano
na slici 15 ona prati prošle greške kvantnovanja i kompenzuje ih kada
kvantuje sledeću vrijednost piksela. Ova metoda mora uzeti u obzir efekte
štampača (slika 15). Koristi se model prekalapanja tačaka. Na svakom pikselu
u slici ovaj algoritam uzima u obzir novopostavljene kolorante. Dok ova
šema proizvodi korektnu skalu tonova takođe rezultuje gubitkom oštrine.
To je zato što novopostavljeni kolorant može biti izvan granica piksela,
dok neki prethodno postavljni može biti unutar piksela. Efektivno ovo
povećava veličinu ćelije SGPM tako rezultujući gubitkom prostorne rezolucije.
Koristi se model preklapanja tačaka koji ozima u obzir samo kolorant koji
je u granicama piksela. Na taj način taj model čuva oštrinu originalnog
algoritma difuzije grešaka. Ovaj rezultujući algoritma se naziva modifikovani
algoritam difuzije grešaka (MED). Blok dijagram ovog algoritma je prikazan
na slici 15. Bez gubitka uopštenosti pretpostavimo da je slika skenirana
slijeva na desno s vrha prema dole. Binarna slika Bij se dobija trešholdingom
„korektne“ vrijednsti Vij gray – scale slike. MED algoritam koristi printer
model da procjeni nivo sivila štampanih slika. Razlika između ovog nivoa
sivila i korigovana gray – scale slike je definisana kao Eij na lokaciji
(i,j). Prethodne greške su filtrirane i oduzete od trenutne vrijednosti
slike da bi se dobila korigovana vrijednst slike.

Prag t je tipično fiksirna na 0.5. MED jednačine su
![]() (15)
(15)
![]() (16)
(16)
za (m,n) < (i,j) ![]() (17)
(17)
gdje (m,n) manje od (i,j) znači da (m,n) ide ispred (i,j) u redosljedu
skeniranja, a
za (m,n) < (i,j) ![]() (18)
(18)
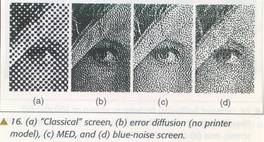
Ovdje su susjedi bkl određeni samo za (k,l) manje od (i,j), pretpostavlja se da su nula za (k,l)>(i,j). Pošto samo doprinosi preklapanja tačaka prethodnih piksela mogu da se koriste u izrazu 18 prethodne greške se i dalje nagomilavaju kako se više binarnih vrijednosti izračunava. To je razlog zašto izlaz printer modela i greška zavise od lokacije piksela. Prepostavka da su neodređeni pikseli bijeli dovodi do odstupanja u gray – scale štampanoj slici. Odstupanje je vrlo malo i teško ga je otkriti u praksi i može se eliminisati višestrukim prolazom MED algoritma kroz sliku. Slika 16 prikazuje uvećane detalje polutoniranih slika onako kako bi bile odštapana na 300 dpi štampaču ako bi se vodile po modelu CDOM sa ρ=1,25.
Difuzija grešaka zavisna od tonova
Ovdje se koriste krivolinijski rasteri i zamjenjuju se prag t sa dva tonski zavisna praga Tzl>Tzu, gdje z označava nivo sivila. Ako je ulaz z manji od niskog praga onda onda je izlaz nula, a ako je veći od visokog praga onda je izalaz 1. Ako z pada između visokog i niskog praga onda se binarni izlaz uzima iz binarne šeme sa apsorpcije 0,5 generisane od strane DBS. Ispitani su svi parametri algoritma da bi se minimizirala funkcija koštanja bazirana na HVS modelu datom sa 12. U međutonovima je nađeno da ova funkcija koštanja nije rezultovala zadovoljavajućom homogenošću i različitosti tekstura tako da je zamjenjna sa ukupnom kvadratnom greškom između spektra snage polutnova generisanih od strane TDED i onog generisanog od strane DBS. Ovdje je funkcija koštanja indirektno povezana sa HVS modelom preko spektra snage DBS polutonova. Generalno TDED može da proizvede teksture polutonova koje imaju skoro isti nivo kvaliteta kao DBS. Zbog velikog broja stepeni slobode koje posjeduje TDED dobar je za korištenje sa printer modelom.
Ostali algoritmi polutnoiranja
Skrining baziran na modelu i polutoniranje sa pretraživanjem tabele
U skriningu binarna slika se generiše poređenjem svakog piksela slike
sa kontinualnim tonovima sa nizom pragova koji su nezavisni od slike.
Binarna slika je crna kada je nivo sivila piksela slike veći od odgovarajućeg
praga i bijela obrnuto. Pragovi mogu biti generisani slučajno ili mogu
biti periodični. Glavna prednost ovih tehnika je što je račun minimalan
i može se izvoditi paralelno. Tradicionalne skriming tehnike koriste osobine
oka samo implicitno. Klasični clusterdot skrim je najpopulanriji za štampanje
zbog svoje robusnosti prema izobiličenjima štampača i sličnosti sa anolognim
tehnikama polutoniranja. Skriming tehnike sa raspršenim tačkama proizvode
slike sa boljom prostornom rezolucijom i boljim teksturama od clusterdot
tehnike ali su osjetljivije na izoboličenja štampača. Ovi skrinovi sa
raspršenim tačkama mogu biti dizajnirani korištenjem bilo kojeg algoritma
polutoniranja. Da bi se mogle implementiranti od strane pragove ove teksture
moraju da se pridržavaju ograničenja tako da jednom kada je crna tačka
postavljena na određenoj lokaciji piksela tačka će ostati uključena za
sve tamnije nivoe sivila. Da bi minimizirali vidljivost osnovnog perioda
u polutonskim šemama i da bi omogućili dizajniranje tekstura boljih kvaliteta
uobičajena je upotreba skrinova koji su veći od 16x16. Veličine 128x128
i 256x256 su tipične. Veliki broj pristupa se koristi za dizajniranje
binarnih tekstura za svaki nivo sivila. Neke od ovih metoda koriste ekspilicitni
HVS model i direktno minimziraju metričku grešku. Takođe je moguće generalizovati
skriming koncept u pristup baziran na pretraživanju tabele koji može proizvesti
određena poboljšanja.
Modeli štampača se mogu se koristiti sa skriming tehnikama tako da uzmu
u obzir izobličenja štampača. Mogu se iskoristiti za modifikaciju pragova
već dizajniranog skrina.
